Mood Brightener: ...more from Stay Homas. (Confination X)

 

Circuits: Conceptual Analysis of 'Simple' Bulb Circuits

From our previous discussion we have a model for how energy is carried by charges from the source of that energy to the destination for that energy. The narrative we developed imagines the source of energy as a donut factory that has an army of small delivery vehicles that fill the roadways between the factory and the destination. The energy delivered (boxes of donuts) depends on how much energy is loaded onto each delivery vehicle and how fast those vehicles are moving down the roadways. This narrative makes it clearer why charges every where in the system begin moving immediately when charges are pushed into the system by the battery/factory. It reinforces the idea that the delivery of energy to the destination (the 'load') depends both on the speed of the charges (vehicles) AND the amount of energy (volts) that each charge is carrying. This model suggests why the energy delivered to the load is different if there are multiple loads in sequence. The model illustrates that the charges exiting the 'factory' must be the same as those arrive back at the factory, that the number of carriers passing a given point on the roadway is the same everywhere, that a break anywhere on the entire path stops the flow of charge, and that anything that affects the flow of charge at one point affects the flow everywhere.

There are still some improvements to the model that we need to make but for now this is a good start. Let's go look at some actual circuits with light bulbs and apply this model. These examples are mostly qualitative (we'll worry about numerical calculations next time) and comparative. Good conceptual exercises!

For the time being we will make certain simplifying assumptions which we can revisit once we get more comfortable with the model. The assumptions are

i) Batteries are the same and ideal and take no energy from the system

ii) Wires are ideal and take no energy from the system regardless of how fast the charges move

iii) All light bulbs are identical.

Because what we are doing is conceptual we need a point of reference. The point of reference is the behavior of circuit I below. If we need a label we can say that the battery is a 12 V (volt) car battery but it could be anything. We usually assume that the charges leave from the (+) end of the battery and return at the (-) end.

Here is our process:

i: Decide how much energy is (still) carried by the charge as it exits the battery, arrives at each light bulb, exits each light bulb, and arrives back at the battery. We will label these as V for volts.

ii: Describe the current at each of the same points. We will label these as I in amps (A) (the traditional symbol for current).

iii: Determine the rate at which energy is being delivered to each load. This involves both the current (flow of carriers) AND the energy delivered (volts delivered). We label this as brightness or power in W (watts).

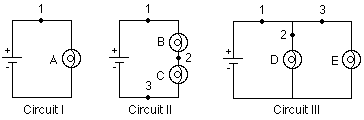
I will apply this model to Circuit I in this video clip.

Circuit II:

Before watching this next video clip apply our process to the circuit and see where you get. Decide how much current you think is flowing through each bulb. How much energy is delivered to each bulb and how bright B and C are relative to each other and relative to A. Once you've made all those predictions you've invested in your thinking in a way which allows you to potentially grow your thinking. No investment no change is kinda how it works:)

Circuit III:

Same again for circuit III. In the end you should have a sense of how all the bulbs in circuits I, II, and III relate to each other in brightness and how much charge the battery provides ('puts on the road') to the circuit in each case.

Model Improvement:

After we have gone through these first three I suspect we will have adjusted our model a little. The particular adjustment I expect is that the more energy the charges deliver to a load the faster they move through it. This is slightly surprising from the perspective of our orginal model but appears consistent with these examples.

We also have an idea now that when there is a junction in the roadway some charges go one way and some the other depending on the characteristics of each path.

In the following image the first two circuits are ones we have already discussed. Apply our model to circuits 3 - 6 and determine the currents, voltages, and brightness (power) of each bulb and compare them to our reference (A in Circuit I above!)

 

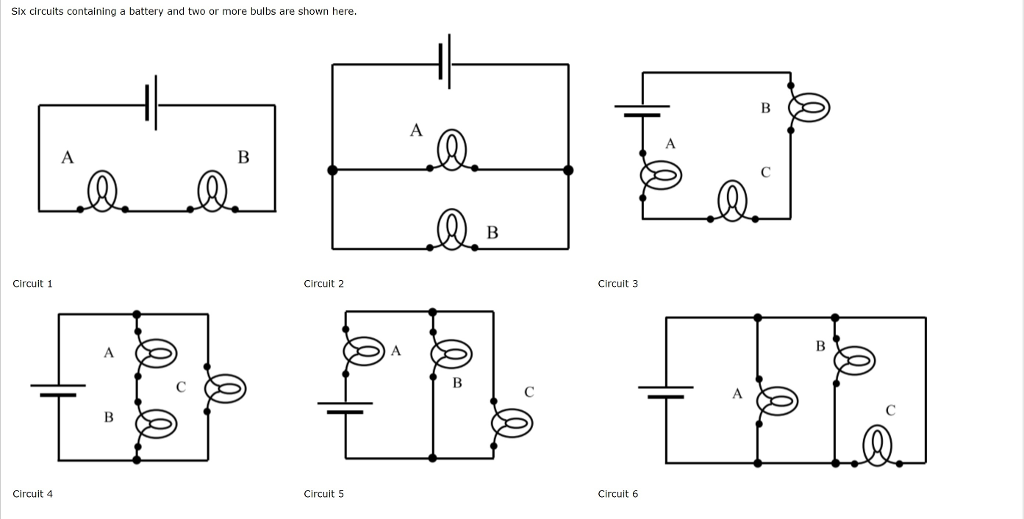
Which of the circuits below match the ones above. Which are new ones? The new ones are slightly more complex. Try one and see what you get. We will discuss in class.

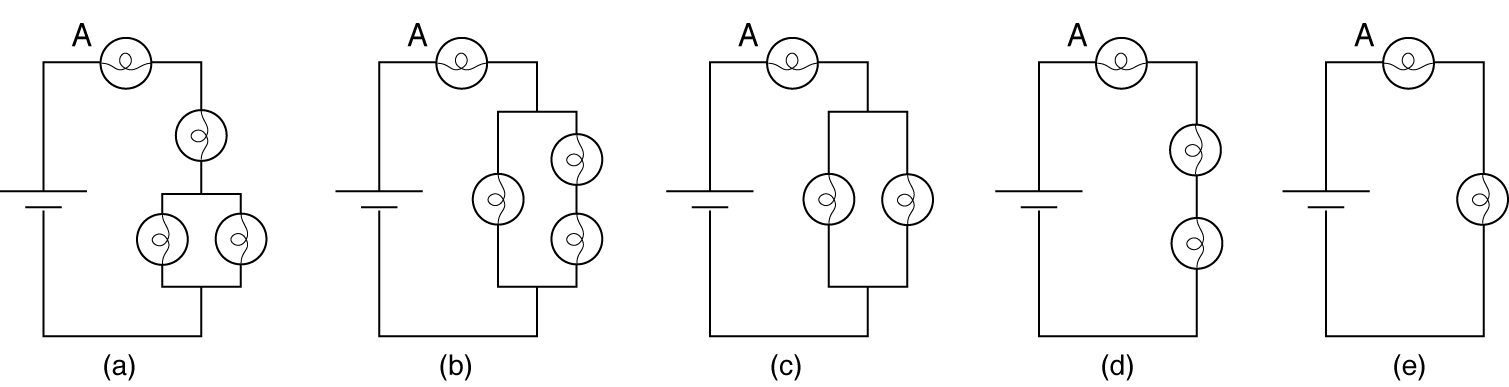
Here's a version of (b).

 

If you want to give it a try here are some complex circuits with 5 bulbs. Our tools will correctly predict what is happening but I suspect we all feel challenged by these.

 

Assignment Breadcrumb Reading: Bb Quiz

Circuit I Concepts:

In our reference circuit (the first Circuit I) consider two (2) questions. If 12 Amps of current enters the light bulb how much current exits the light bulb? If the charges are carrying 20 V of energy when they enter the bulb how much are they carrying when they exit the bulb?

Before Next Class:

Assignment HW: Bb Quiz

Circuit 4:

In circuit 4 of the examples (there is only 1 circuit 4 I think) rank the brightness of the bulbs from brightest to dimmest. A possible solution is A = C > B.

Assignment HW: Bb Assignment

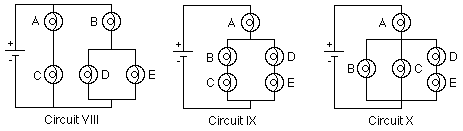
Circuit VIII:

Apply our analysis to Circuit VIII above showing currents, voltages, and brightness for each of the bulbs.

Looking Ahead:

Look ahead to the next Breadcrumb:

Assignment Breadcrumb Reading: Bb Quiz

Why Turn It In To Math?

Why do those physicists have to turn everything into math? Why does writing down our conceptual understanding in mathematical terms add value?