Introduciton:

This 5 min video is a great introduction to the core concepts of light and EM waves (light is an EM wave). Thanks NASA!

Light

Light is how we 'see' things. 'Seeing' is what we call the detection and mapping of where the some kind of light is coming from. Our eyes, combined with the processing of the information detected by our eyes, forms a map or image that we use to understand and interact with the world around us. Things that we 'see' either generate light that our eyes detect (fires, light bulbs, LEDs), they reflect some other source of light towards our eyes to be detected, or the pass through various materials on their way to us. The color of objects that emit light depends on the process that creates the light. Stars emit light and can look yellow, blue, red, or even green. LED lights and incandescent bulbs emit light that looks quite different to us. Our perception of reflected light depends on both the source of the emitted light and the surface it is reflected from. Most surfaces absorb some colors of light. A wall looks blue when all the colors except blue are removed from the light hitting the wall. Sometimes the light passes through some material on it's way to our eyes and that material affects which colors of light get through. An example is the red sun at sunset. It's the same sun we see during the middle of the day but the more atmosphere it goes through the more blue like is removed leaving the sun looking red.

Major Characteristics of Light:

Speed, wavelength or frequency (which are related to color), and brightness. Light can be absorbed or emitted differently in different circumstances. We'll take each of these in turn.

Speed:

As you may have heard the speed of light (in a vacuum) is constant. We often don't notice the 'in a vacuum' part of this statement. The speed of light in a vacuum is generally labeled with a special symbol - c - because it's so important in our modern understanding of the world. c = 3^.10⁸ m/s. Light does slow down in different materials though it never goes faster than this as far as we know. In air it moves very nearly the same speed as in a vacuum but it's only half as fast in a diamond. Since space is mostly a pretty good vacuum so we take the speed to be c.

Basic Structure?

Light is a very complex creature in our modern world. It behaves very differently in different circumstances. In most cases that we experience it seems to behave like an ocean wave yet in some circumstances (solar panels are an example that you have seen) it behaves like a particle. This raises an interesting philosophical discussion about what it actually 'is'. For now we want to explore what it means to say light is a wave.

As a wave here is how we think about light...

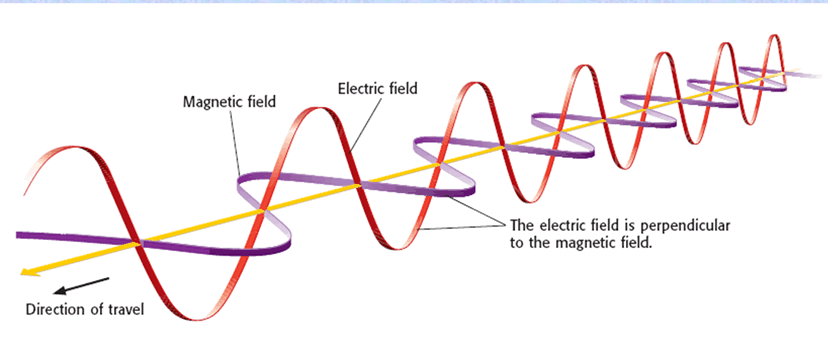
As you can see there are two parts to a light wave each of which is 'waving'. There is an electric part (made of the same electric fields that push charges through wires in our houses) and a magnetic part (which can be created by magnets or by electric currents in motors). These two parts are perpendicular and collectively perpendicular to the direction the light is going. Simple looking but complicated to explain. This is why light is called an electromagnetic wave or EM wave.

An interesting question to ask is 'What is waving?'. We're pretty clear about what is 'waving' in ocean waves that would be the ocean. What is 'waving' in sound waves? What is 'waving' in seismic waves? What could possibly be 'waving' in the emptiness of space? I'm not concerned that you have a crisp answer for this but rather that you notice that apparently, in the nothingness of space, something is waving. [for those of you who just have to know the fields are waving but even that is an incomplete answer]

Wavelength and Frequency:

This is a good place to think about your experiences at the ocean. When you stand at the edge of the ocean we are generally very conscious of the distance between the crests of the waves. That distance, from crest to crest, is what we call the wavelength.

You are also very aware, particularly if the water is cold, that there is a time that elapses between when one wave crest hits you and when the next wave crest hits you. That lag time is called the period between the wave crests. If you think about it the next crest of a wave has traveled 1 wavelength to get to you in 1 period. Symbolically we represent the wavelength with lambda (λ) - think of the 'l' in lambda connecting to the 'l' in length - and we represent the period with T because it's a time. This allows us to be more explicit about the mathematical relationships.

Thinking back to the ocean again perhaps you can visualize each wave crest moving forward 1 λ in a time T. That means we know how far it went in how much time. Since speed = distance/time we can describe the speed of the wave as

v = λ/T => c = λ/T

T (period) is the number of seconds need to complete one cycle (s/cycle) of the wave which makes sense for ocean waves. Sometimes the waves are traveling so fast or have such short wavelengths that it makes more sense to talk about the number of wave cycles completed in each second. Sound is this kind of wave. Middle C, in the middle of the piano, is a sound wave where the crests run into your ear 256 times each second (256 cycles/s). We call this the frequency and label it with the symbol f. The units of frequency, cycles/s, are called Hertz and abbreviated Hz. Where have you seen this before? You may notice that the units for T and f are the inverse of each other.

T (s/cycle) and f (cycles/s) which means mathematically T = 1/f or f = 1/T

All of this leads us to a very useful relationship:

 

c= 3.0 10⁸ m/s = λ/T = λf

 

This is the first mathematical tool you should consider for calculations with waves. Why, you may well ask, is this important? For starters it means that if we know λ we can figure out T and f or conversely if we know f we can figure out λ and T

For reasons that have to do with other parts of science it turns out that it is hard to detect a wave with an instrument that is smaller than it's wavelength. Knowing the wavelength of different kinds of light is important for building 'telescopes' for looking at this kind of light.

Electromagnetic Spectrum:

Now that we have a sense of what these terms mean lets look at the many different EM waves that are out there. This is a huge graphic but it makes it easier to see and understand the different parts. Another version of the EM spectrum is underneath and gives a slightly different representation. Thanks to Wikimedia for the use of both.

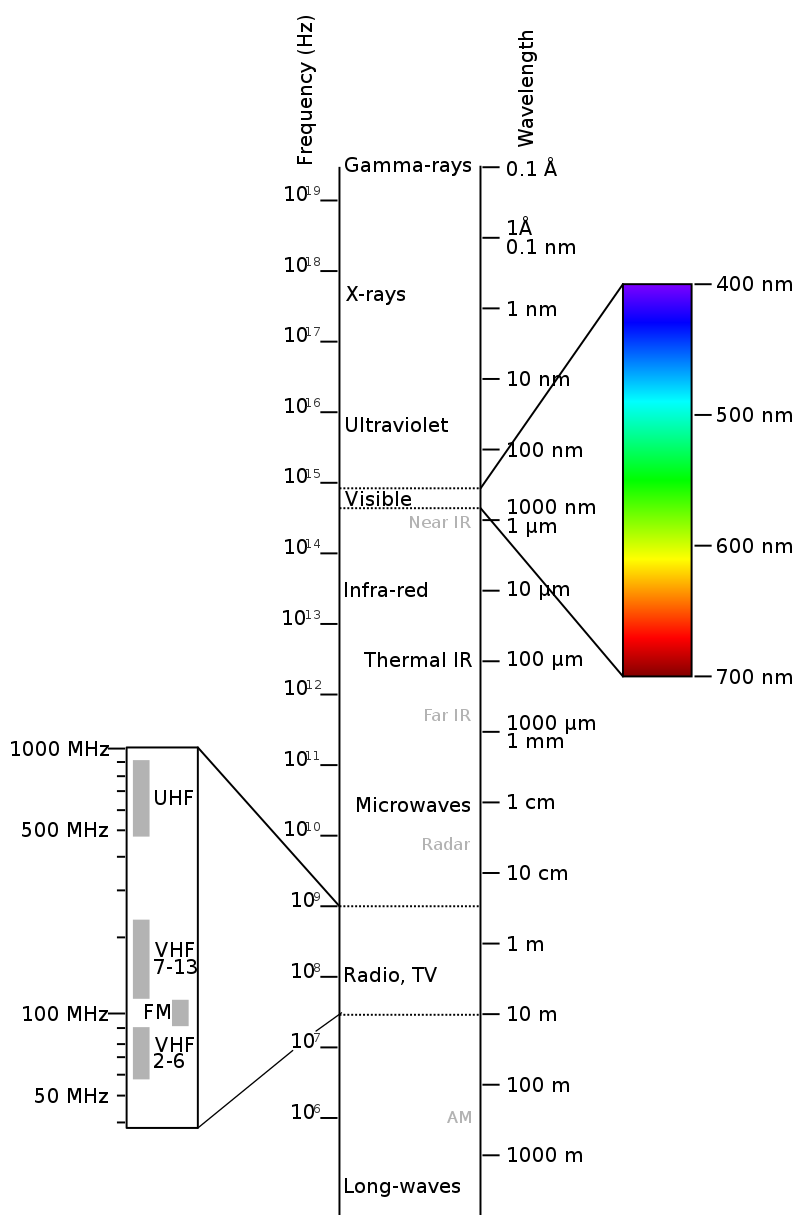
..and...

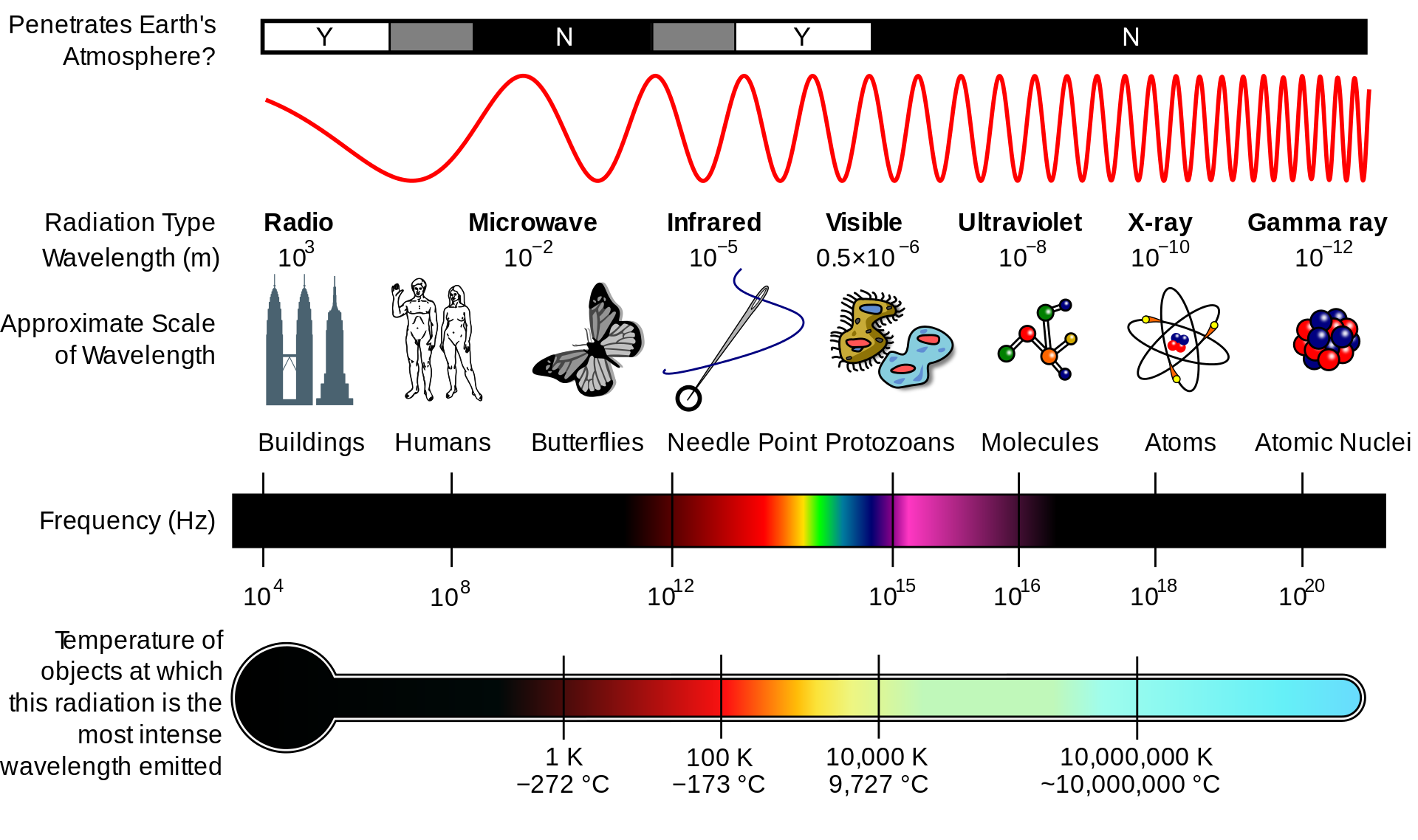
Activity: Explore the EM spectrum and find the following 'light' waves. Notice their wavelength. How big is the object we use to detect that wave?

FM radio waves

radar for weather and airplanes

red light?

HW: Waves

What is the frequency of light that has a wavelength of 1 mm - roughly? Looking at the EM Spectrum is this a radio wave, ultraviolet, infrared, or a microwave?

HW: Waves

Are shortwave radio waves longer or shorter than AM radio waves? Explain your reasoning. You may have to do a web search to find out what typical short wave radio frequencies are. Given that a typical antenna is λ/4 what length do you expect for your friends shortwave antenna?

Color:

You are well aware that light comes in different colors since you see them around you all the time. Our eyes are have different sensors for different colors but generally we can see from red to blue which covers all the colors in the rainbow. We generally describe those colors in terms of their wavelength which run from 700 nm for red light to 400 nm for a blue bordering on UV.

Thanks to the BBC

If I had the special eyes of the mantis shrimp and could see light that is UV where would I see it in the rainbow above? If I could see infrared light where would I see it in the rainbow?

Since we're talking about rainbows this is a good time to take an aside and do a little math practice with waves.

Activity: What is the rule that you were taught in your family about figuring out how far away lightning is from the sound of the thunder? There are usually many rules and I just want you to figure out which one is used in your family and see what others learned.

HW: Waves

Thunder and lightning: In class we used the speed of light waves (c = 3^.10⁸ m/s) and the speed of sound waves (v_sound = 343 m/s) to figure out the rule the tells us how far away lightning is. Starting with a clear sketch reproduce that calculation and state your own version of the rule. Your statement of the rule should allow me to easily determine when lightning is 1 km (roughly 1/2 a mile) away as well when I'm in Europe.

You may be aware that some animals see 'colors' that we don't and the world looks a little different to them. Imagine if we 'look' at the universe using as many of these different colors as possible.

Color and Temperature:

There are a number of places where you may have seen reference to color being connected to temperature. One of these is the color temperature rating of lights. The higher the temperature rating (5500 K) the bluer the light is. The cooler the temperature is (3500 K) the warmer or yellower the light is. You also know if you look at a piece of hot metal that a dull red color is hot but where it's more white it's much hotter (see image below - thanks to Wrought Works for the use of the image)

This relationship between the temperature of an object and it's color is the result of a process called blackbody radiation. Every object has a range of 'colors' of light that it emits that depends on its temperature. This is, in fact, how the non-contact thermometers that are use to check your temperature for COVID infection work. Here are the blackbody curves for a number of temperatures showing the range of human detection as well. The vertical axis indicates the relative amount of light of a particular wavelength being emitted by the hot object.

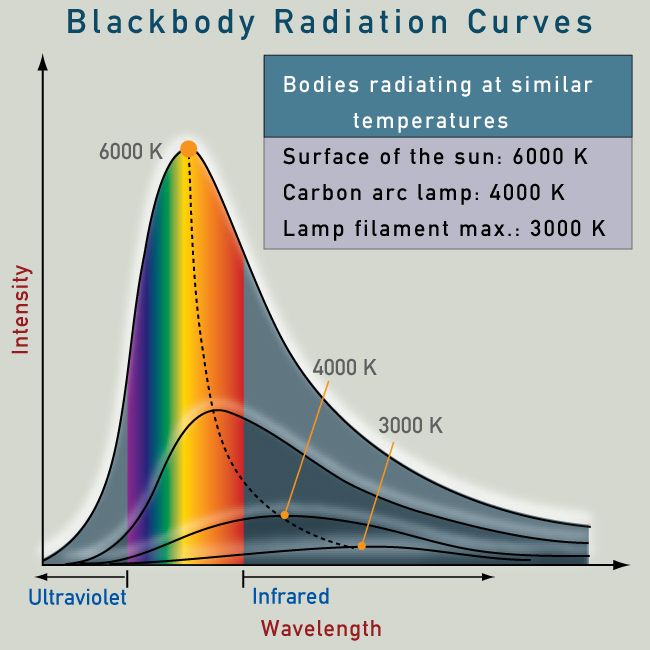
Notice that at 6000 K the peak of the curve spans the sensitivity of the human eye. We see light like this as white because of the way that mix of colors interacts with our eyes. As the temperature drops notice that the peak of the curve moves towards the red end of the visible spectrum. This is consistent with our experience that white hot objects are hotter than glowing red objects. As the objects get even cooler it still emits lots of light in the infrared but only a tiny amount of very red light making the object look mostly dark (because we can't detect the light) with a little sense of dull red.

Activity: What would you expect light from a 8000 K object to look like?

We can build cameras that 'see' infrared light that we can't see with our eyes. This is the image of a house where the 'warmer' the color the hotter the surface is. This can be used to see where heat is leaking out of a house. The roof on this house is pretty good but the upper walls facing the street are quite warm.

Composite Images:

The ultimate goal of a richer understanding of these basic features of light is to create composite images of objects we observe in Astronomy using different wavelengths of light. In this process we can gain insight into the distinct processes that generate light of different wavelengths. More about that next time. Below is a set of images of our sun taken using only light of particular wavelengths. The wavelength is labeled in yet another unit call and angstrom which has that unusual symbol - Å. 10 Å is 1 nm so if you move the decimal place LEFT 1 place you will have nm. What do you notice about the wavelengths of most of the images?

This image shows the Crab Nebula as it appears when 'looked at' with different wavelengths of light.

Assignment: HW Waves

Complete and assemble your solutions to all (3) the HW problems listed here. Scan to a pdf and turn in on LMS. Please review HW format expectations for guidance about your homework solutions.

Reading Ahead:

Next time we will begin our explorations of light via the Light II breadcrumb. This will get us into the topic of emission and absorbtion of light.