You might well wonder why anyone would want to learn how to estimate more effectively, sometimes called Fermi problems, when you could just use mathematics to figure out the answer 'correctly'. It turns out that there are a whole range of circumstances where estimation is the only effective way to address a poorly defined problem. In engineering classes a quick estimate of the net force vector can give you a sense of both the magnitude and direction of the reaction force you are seeking. One of my physics heroes, Rhett Allain (see below), who does a lot of estimating was the first person to correctly estimate the amount of oil leaking out of the Deepwater Horizon in 2010 and influencing the subsequent recognition of the scale of the disaster. Practicing estimation also strengthens ones math and physics skills both conceptually and practically and it's often just fun. The National Science Foundation recently funded an astronomy project that included a goal of enhancing the estimation skills of teachers in STEM disciplines through workshops at Dartmouth College and other locations. If you wish to seriously explore developing some serious estimation skills I recommend Sanjoy Mahajan's Opencourseware course called 'Streetfighting Math' which is sometimes offered through edX. At a higher level of mathematics you might also find 'Consider a Spherical Cow' and 'Consider a Cylindrical Cow' by John Harte of interest for his use of differential equations to understand complex biological and environmental systems.
Why Estimation?
Let me start with some ideas from others who are more articulate about this. Here is Sanjoy Mahajan from the preface to his book on complexity and insight. Links to this book and other estimation resources can be found on the Web Resource page for Estimation.
"Science and engineering, our modern ways of understanding and altering the world, are said to be about accuracy and precision. Yet we best master the complexity of our world by cultivating insight rather than precision.
We need insight because our minds are but a small part of the world. An insight unifies fragments of knowledge into a compact picture that fits in our minds. But precision can overflow our mental registers, washing away the understanding brought by insight. This book shows you how to build insight and understanding first, so that you do not drown in complexity.
Therefore, our approach will not be rigorous—for rigor easily becomes rigor mortis or paralysis by analysis. Forgoing rigor, we’ll study the natural and human-created worlds—the worlds of science and engineering. So you’ll need some—but not extensive!—knowledge of physics concepts such as force, power, energy, charge, and field. We’ll use as little mathematics as possible—algebra and geometry mostly, trigonometry sometimes, and calculus rarely—so that the mathematics promotes rather than hinders insight, understanding, and flexible problem solving. The goal is to help you mas-ter complexity; then no problem can intimidate you."
This helps make sense of this insightful statement from one of his students:
"I used to be curious, naively curious. Now I am fearlessly curious. I feel ready to attack any problem that comes at me, and at least get a feel for why things happen … roughly. "
Here's different take from David MacKay (author of Sustainability without the Hot Air) who passionately believes in rough estimation as a primary tool for assessing a problem in the begining (he is also a pal of Sanjoy). He is talking here about the way in which numbers are used, or not, in the discussion of energy issues.
" Where numbers are used, their meaning is often obfuscated by enormousness. Numbers are chosen to impress, to score points in arguments, rather than to inform. “Los Angeles residents drive 142 million miles – the distance from Earth to Mars – every single day.” “Each year, 27 million acres of tropical rainforest are destroyed.” “14 billion pounds of trash are dumped into the sea every year.” “British people throw away 2.6 billion slices of bread per year.” “The waste paper buried each year in the UK could fill 103,448 double-decker buses.”
If all the ineffective ideas for solving the energy crisis were laid end to end, they would reach to the moon and back. . . . I digress.
The result of this lack of meaningful numbers and facts? We are inundated with a flood of crazy innumerate codswallop. The BBC doles out advice on how we can do our bit to save the planet – for example “switch off your mobile phone charger when it’s not in use;” if anyone objects that mobile phone chargers are not actually our number one form of energy consumption, the mantra “every little helps” is wheeled out. Every little helps? A more realistic mantra is:
if everyone does a little, we’ll achieve only a little."
Finally, I'd like to draw from some material written by another hero of mine - Rhett Allain. He writes a blog about physics and estimation for WIRED but recently they have gotten uptight about open access so I will quote him here.
" The art of estimations is pretty much a physicist's bread and butter. We all love a good estimation problem. You might also hear these called a "back of the envelope" calculation, or a calculation on a napkin. The writing medium is meant to emphasize how little preparation goes into attacking the problem. The estimator can't even take the time to find a clean sheet of paper.
But these calculations aren't just for fun, they are also useful. One good example is a question that I just recently calculated: How big of a balloon would you need to lift a human?
Woah! Right there people might be saying: But wait! Is this a hot air balloon? Is this a hydrogen balloon? What material is it made of? The answer is "I don't know, I don't care." The true power of the estimation problem is that you can pretty much ignore things that you don't know. Yes, this takes some practice to figure out what is important and what isn't.
You have to start with something. There has to be some estimate or physics principle that you start with. You can't just estimate the mass of the moon if you don't know anything about gravity or how long it takes for the moon to orbit the Earth. [In the example above,] I just happened to know the density of air because I've used it before. I also knew the relationship between buoyancy and the size of an object (Archimedes' Principle). Without that, I would be pretty much stuck.
Estimation problems are sort of like a rough pencil sketch. It doesn't have all the exact details of a photograph, but it's enough to give you an idea of what's going on."
Why Engineers?
You would be right to notice that many of the folks I have cited in this discussion are physicists and not engineers. I might argue that they are all very much applied physicists which is not particularly different than an engineer but I accept the point. It is a reasonable question how this skill of estimation is relevant to engineering. A number of years ago we had an instructor here at COCC who came to us from a large engineering firm in Seattle. She noted that she had regularly been asked to estimate, in the field on the spot, the probable characteristics of the engineering solution to a design problem. Her boss insisted that she provide a response without resorting to long calculations at her desk later. As a result estimations were a required element of engineering solutions in her class. I have had similar conversations with engineers currently employed in the commercial space industry. The rationale of these engineering practitioners for being able to estimate mirrors that of the physicists above.
What Bruce thinks:
Well....not sure how much it matters what I think but here's what I'd like to add to the discussion. In my experience the ability to successfully estimate features of a physics or engineering problem is closely tied to the strength of my conceptual understanding of the underlying principles. If I find that I am having trouble with an estimate it is usually because my conceptual understanding of the situation is shakey. Conceptual understanding is what gives all of us the ability to transfer our understanding from one setting to another.
Estimation also asks us to makes decisions about what is most important in a particular setting and not get distracted by the details. In the end the details will be important but they are rarely important at the begining.
Basic Methodology:
Break it into Chunks!
Questions that take one step to get to the answer are hardly interesting. Most real questions involve multiple variables and concepts. The first step in addressing the question is break it up into smaller more approachable chunks. Sometimes we can see these chunks by considering the units of the answer (an early indication that paying attention to units is important!) Consider the question of the density of snow (in the HW in the Concepts breadcrum b) -- what is density? ... kg (mass)/ volume .... I need to estimate a volume and then the mass of that volume .... to get a volume I need 3 chunks - width, height, and length. To get a mass I need to know what it feels like when I pick up the snow compared to a known object (another chunk).
Activity: Compare your solution to the snow density problem with other students. Nobody is right or wrong unless you get a density larger than water or less than 10 kg/m3. Consider all the different ways people approached the problem.
Build the Tree!
We also need a strategy for keeping the various chunks organized. A tree diagram is a useful way to organize things. Below is a tree that addresses part of the question of estimating how many barrels of oil the US need to import each year.

This image is taken from
The Art of Insight in Science and Engineering: Mastering Complexity
by Sanjoy Mahajan which is licensed under the CC-BY-NC-SA 4.0 License.
Notice that the tree also helps organize the units which are helping to suggest where there may be missing chunks. I would draw your attention to the bottom right corner. How did the process determine that a barrel is roughly 60 gallons? You can imagine that a barrel is like the barrels you see along the road which is where you might get the 1m x 0.5m x 0.5m (why not a cylinder?) but where did the 250 gal/m3 come from? The underlying knowledge from the ISU system of units is that 1 m3 is 1000 liters. If you imagine that a liter is about 1 quart then there would be 250 gal/m3. My point is that there are some very useful bits of general knowledge that can help.
Some practice problems:
Problems of this types are sometimes referred to as Fermi problems after Enrico Fermi (one of the fathers of the atomic bomb) who had a fascination with estimation problems.
Warming Up:
What is the volume of a penny? ...a dollar bill?
How does the number of pennies it would take to carpet the state of Oregon compare to the national debt of the US?
What is the value density of $20 bills compared to gold? This has the utility of telling us whether whether a Brinks truck loaded down with gold is a better target than one loaded with paper money. There are two distinct value densities we can calculate -- value/mass and value/volume. Do both.
How many seconds in a human lifetime? Of course this can be done with some exactness but leave your calculator alone and see what you get. How does this help us think about what $5 billion is?
Activity: We will pick a couple of these problems to explore in groups during class.
HW: Estimation
Here is a link [https://www.youtube.com/watch?v=2xFji9-xgMw ] to some security video of a Tesla going a little fast and getting airborne due to a railroad crossing. Estimate the velocity of the car in m/s. In your solution be sure to be very clear about your assumptions and units.
[50 m/s]
HW: Estimation
Here is a link to the engineering specs for the retractable field at University of Phoenix Stadium. Given the data what is a reasonable estimate of it's travel speed in m/s? We will revisit this later in the term to consider what the 76 1 hp motors tell us about friction as it moves. This is an impressive piece of engineering.
[4 .10-2m/s]
HW: Estimation
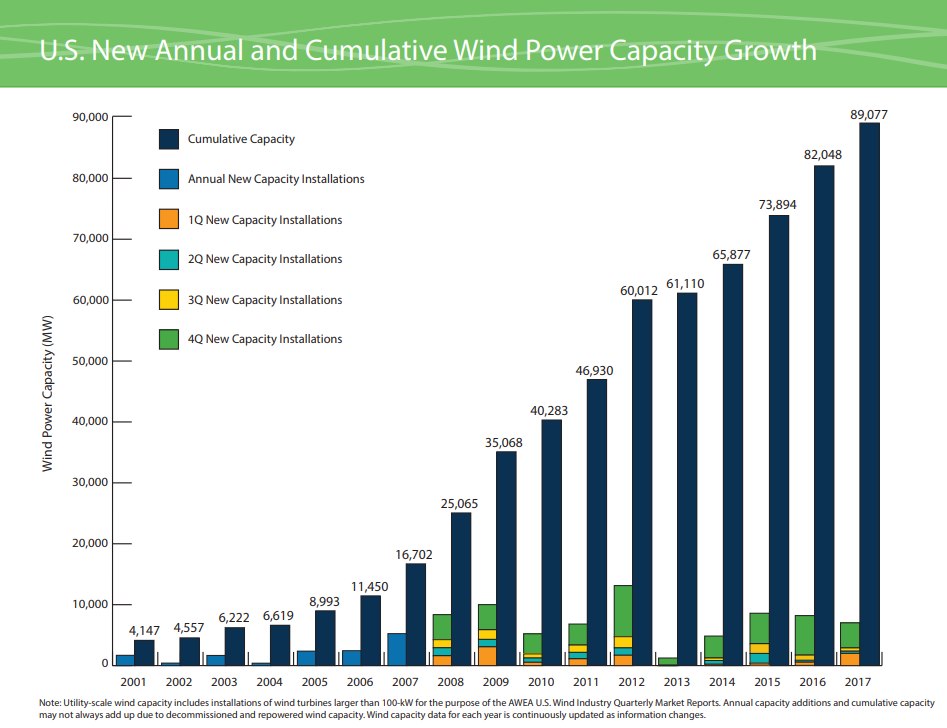
Consider the plot below that shows the installed wind turbine capacity for the US.
Estimate the rate at which we are installing wind turbines over the last decade in GW/yr. Does the data suggest it's pretty constant? What would you estimate the rate of installation was in 2006? Think about this last question from a calculus perspective and instantaneous slope. Finally, we will need about 4.3 TW of additional installed wind turbines if we want to replace ALL of our energy use with wind generated electricity. At the rate we've been building this last decade how long would it take to reach this goal?
[around 7 GW/yr, 3 GW/yr, 500 yr-ish]
Assignment: HW: Estimation
Turn in the various (3) homework problems in this breadcrumb. For these problems please use the problem solving format described in the Concepts breadcrumb.
Assignment: Reading
Go on to Newton's Laws 1D breadcrumb to move to our introduction to the core physics tools for this term.