Momentum:
One of the things I would like you to notice about this unit and the previous one on energy is that they both start from the perspective of exploring ways that we can apply our understanding of Newton's 2nd Law to different settings. In the case of energy we asked about the effect of a force acting over some distance on the characteristics of an object. In the case of momentum we start the same place but approach things from a temporal perspective.
Impulse:
The typical starting point for this discussion is to consider the impact between two object like a bat and a ball or a hockey stick and a puck or a watermelon and the ground. The plot of the force on the object being whacked would look something like this....
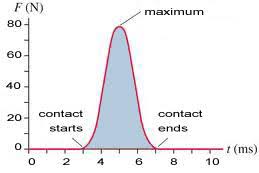
As we often do with data we ask what the area under this curve might mean. Setting up the integral and considering the terms we see.....
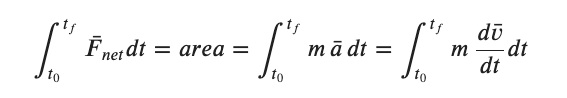
As we have seen before we can treat the derivatives and differential elements as fractions as long as the functions are well behaved. Looking at the last term above we can follow it a little further to get.....
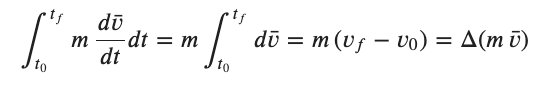
Cleaning all of this up we get....
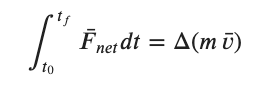
Because we generally associate these sorts of situations with short term applications of forces to an object we have historically labelled both the integral and the change in the quantity mv as the impulse. J is a common symbol though not the only one. This leads to....
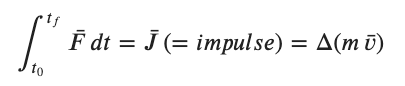
While we started by thinking of this as a plot of Fnet the concept is also applied to individual forces. Notice that, unlike our previous discussion of energy this quantity is a vector which means it has components to consider and any signs indicate direction as in other vector quantities.
As with any integral we can define an average force which is constant. Plotting such an average force on the plot above would create a rectangle which has the same area as the integral. Mathematically we say....
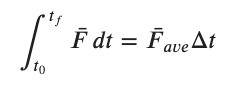
The Result:
Putting all of the above together we get a lengthy expression which describes the relationship between forces over time, impulse, and the change in the quantity mv.

Momentum:
While it might be a little premature it turns out that this quantity mv shows up again and again and is an important feature of an object or collection of objects. For this reason we give mv it's own name. It is called the momentum whose symbol is usually lowercase p. Note that the momentum is a vector that points in the same direction as the velocity but is scaled by the mass. Momentum has units of kg-m/s which has, surprisingly, not been given it's own name.
![]()
Problem Solving:
An important thing to notice is that the expression above describes the force(s) on a SINGLE OBJECT. When we talk about forces applied over a time we describe them as IMPULSIVE FORCES. Any of the 4 terms in the expression above are called the impulse.
The shape of the plot of the impulsive force is pretty typical and in rough terms the peak force, Fpeak, is about 2x the average impulsive force Fave.
HW: Momentum 1D
You have two objects each of which has a mass of 250 g. One is a sticky lump of clay and the other is a very bouncy ball. When you throw them both at a wall at 3.0 m/s the clay ball sticks to the wall and the bouncy ball comes back at 3.0 m/s. In both cases the collision lasts for 20 ms. What is the average impulsive force on each ball? Which one applies a greater force to the wall (a 3rd Law question)?
HW: Momentum 1D
Another classic example of impulsive forces is when a ball player strikes a ball with a bat. A baseball has a mass of 145 g. Assume that the incoming pitch is traveling 40.0 m/s and the ball leaves the bat at 49.0 m/s (realistic numbers) and that the ball is in contact with the bat for 0.8 ms. What is the average impulsive force experienced by the ball? How many "g's" is this?
Systems of Objects:
Up to this point in this course we have generally considered forces as applied to individual objects. Even when we consider groups of objects we have been seeking to understand the effect of unbalanced forces on the group of objects. Lets start by restating Newton's 2nd Law in a slightly different way....
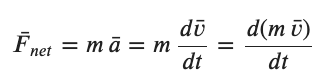
As you are aware the equivalence between m (dv/dt) = d(mv)/dt = dp/dt is only valid when the mass is constant. Just a note for the future -- d(mv)/dt is the actual form of Newton's 2nd Law and we will explore the (dm/dt)v term next year in dynamics. If we more carefully label this we might say...
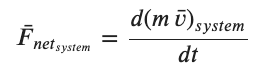
The context in which the ideas of momentum are typically applied is when two objects collide. In this setting the net external forces are often 0 (since internal forces between the objects cancel in a vector sense due to Newton's 3rd Law) or negligibly small. When the net forces on a system are zero interpretation of our usual F = ma version of Newton's Law gets a little confusing since this implies the acceleration of the system is 0 and in a collision this can be hard to understand. While we will not explore this idea to any extent it can be understood as saying the the acceleration of the center of mass of the system is 0. If there are no net external forces on my chosen system then....
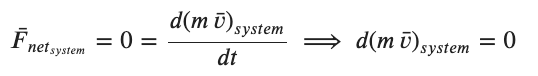
If the derivative of the momentum is 0 that means dp must be 0. This means the momentum of the system evaluated at any two points in the process must be constant.
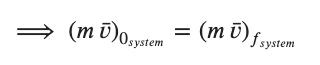
When we consider the momentum of a system we mean the sum of the individual momenta of each object in the system. Be careful.... these are vectors so directions and components are relevant!
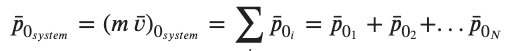
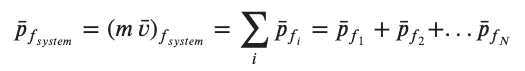
The form in which we usually express this relationship which is only valid when there are NO NET EXTERNAL FORCES, is below.....
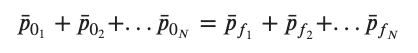
This expression has a lot of similarity to the conservation of energy equation from our previous discussions. Not surprisingly we will use a similar bar graph to visually represent this equation. The following structure is for two objects moving along a single (x) axis.
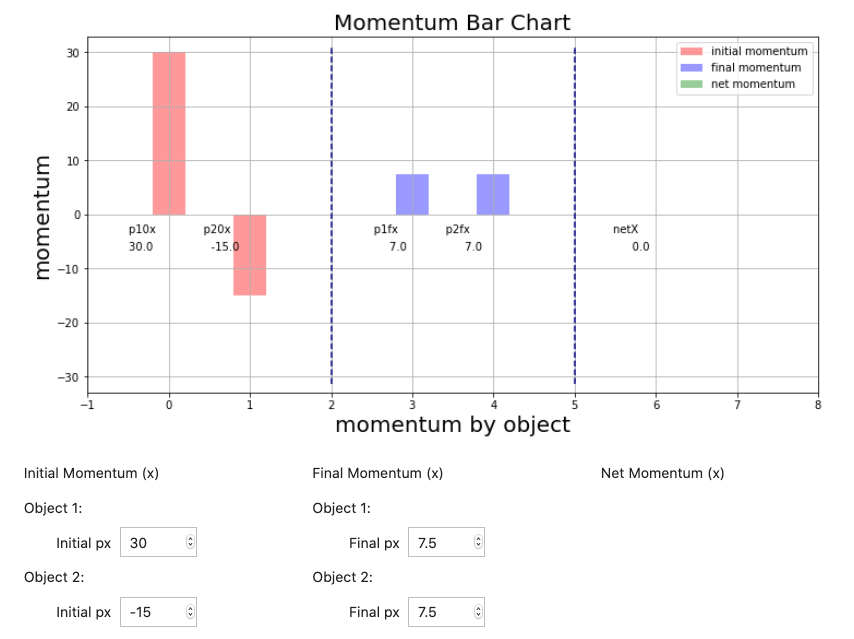
If we enter values into this bar chart the netX value will confirm that momentum is being conserved along the indicated axis.
HW: Momentum 1D
In a sci-fi book called Ender's Game by Orson Scott Card (yes it's a movie) there are two kids fighting in a zero gravity environment. They are initially stationary but as the result of pushing each other Bonzo flies off at 1.5 m/s while Ender recoils at 2.5 m/s. Remember that momentum is a vector quantity. What direction is Ender moving relative to Bonzo? Which kid is heavier? What is the ratio of their masses (mB/mE)?
Assignment: HW: Momentum 1D
Turn in the various (3) homework problems in this breadcrumb. For these problems please be attentive to our problem solving format and guidelines for different styles of problems.
Assignment: Reading
Now that we have the basic ideas of momentum on the table we'll move on to collisions in 1D and 2D which just adds some algebraic excitement. Read the Momentum II breadcrumb.
