Momentum: Collisions/Applications

Applications: Collisions

The classic collisions that we want to be able to consider are those between two objects that may have different masses and velocities. One dimensional collisions mostly fall into one the the following categories.

One Object Moving - 'sticky': (same mass, one heavier - one lighter)

One Object Moving - 'bouncy': (same mass, one heavier - one lighter)

Both Objects Moving Towards Each Other - 'sticky': (same mass, one heavier - one lighter)

Both Objects Moving Towards Each Other - 'bouncy': (same mass, one heavier - one lighter)

Here is a video that demonstrates the collisions described above in the cases where the masses are the same. While it's relatively easy to do the demos with mismatched masses I don't find any compact videos on the web at the moment.

The examples described and illustrated above represent two classes of collisions. These are loosely labelled sticky and bouncy. Since we can't talk in public like that we need to tighten those descriptions up and give them names that make them seem more sciency! It turns out that the distinction between these two extremes is really about conservation of energy. In sticky collisions there is a contact force applied over a distance as the object deforms and sticks which takes energy away from the system. Bouncy collisions describe collisions between rigid objects where there are large forces but almost no deformation of the objects (no Δx) which means no energy is removed.

In formal physics terms these are called inelastic (sticky) and elastic (bouncy). Both collisions conserve the momentum of the system and elastic collisions ALSO conserve energy.

Problem Solving:

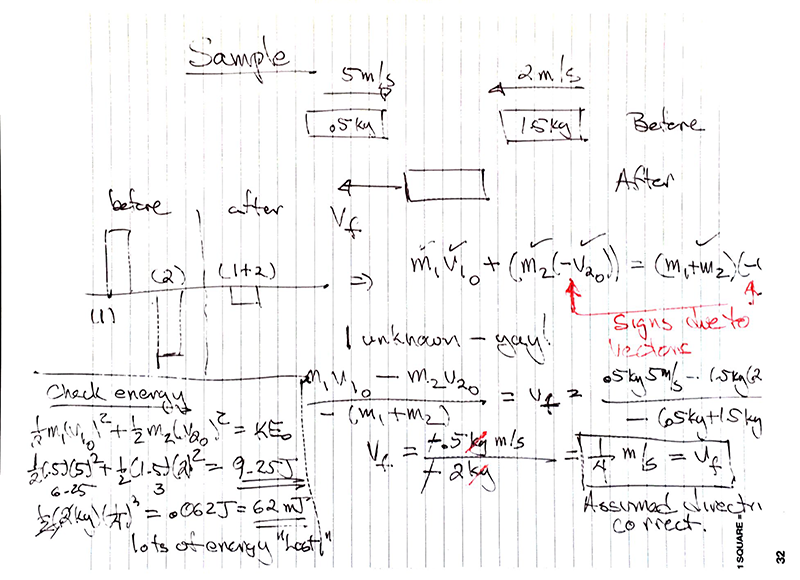
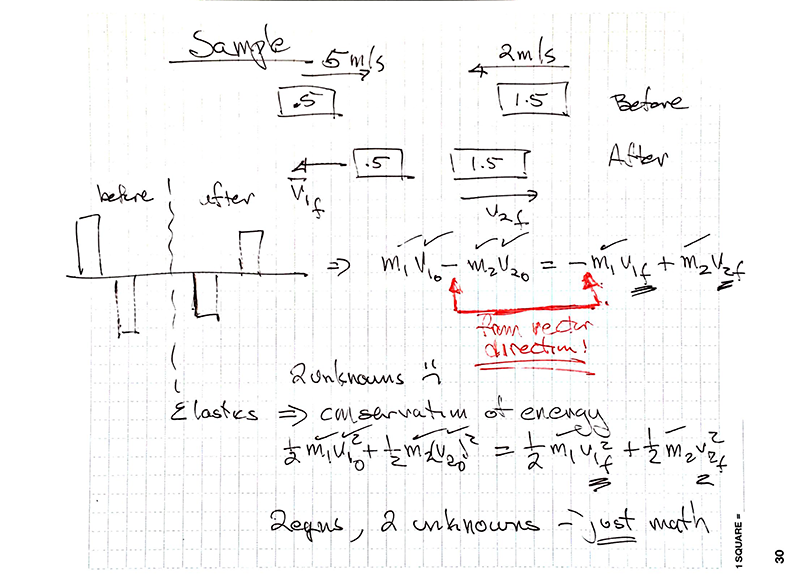
As always we start every physics problem with a sketch. In this case the sketch will have two parts. What is happening just before the collision and a second sketch illustrating what is happening immediately after the collision.

After the sketch a best next step is to sketch out a momentum bar chart to guide the creation of the conservation of momentum equation.

Once you have the bar chart write appropriate equation(s) and assess whether you have enough information to solve the problem.

If you consider the energy bar chart in the previous breadcrumb you can imagine that we might well know the velocities of both objects before the collision and are interested in their respective velocities after the collision. When we write down the conservation of momentum equation from the bar chart we will have two unknowns. This makes the problem unsolvable unless we have some additional information.

In the case of an inelastic (sticky) collision there is only one final velocity because the objects are stuck together. In this case the equation is usually solvable.

In the case of elastic (bouncy) collisions we have an additional useful bit of information which is that the kinetic energy is conserved. This gives us an additional equation with the same two unknowns (the final velocities of each object. Again, the problem is solvable because we have two equations and two unknowns. The algebra can be hideous due to the squares in the kinetic energy equation but it's just algebra!

Example Sticky:

Imagine two objects moving towards each other along the x axis. Object 1 has a mass of 0.5 kg and a velocity of 5 m/s in the + x direction. Object 2 has a mass of 1.5 kg and a velocity of 2 m/s in the -x direction. They collide inelastically. What is the velocity of each object after the collision?

Example Bouncy:

Imagine two objects moving towards each other along the x axis. Object 1 has a mass of 0.5 kg and a velocity of 5 m/s in the + x direction. Object 2 has a mass of 1.5 kg and a velocity of 2 m/s in the -x direction. They collide elastically. What is the velocity of each object after the collision?

HW: Momentum Applications

In the James Bond movie Diamonds Are Forever one of the characters is driven off the edge of an oil rig by an automatic weapon she is shooting the place up with. The mass of the bullet is 10 g and it's muzzle velocity is 720 m/s. If her mass is 51 kg what is her change in speed (from rest) due to the first bullet fired? What is her change in speed for the second bullet?

HW: Momentum Applications

A golf ball (m=50 g) is fired at a stationary bowling ball (m = 7.3 kg) at 32 m/s and bounces straight back at 90% of its initial speed. In this collision of rigid objects which has the greater kinetic energy after the collision? Which ball has the greater momentum?

HW: Momentum Applications

A 10 g bullet is fired straight up into a falling block of wood with a mass of 2.0 kg. The bullet is traveling 750 m/s when it hits, and embeds itself, in the block. As a result of the collision the block, which was dropped from the top of a building, reverses its direction and rises until it comes to a stop level with the top of the building. How long had the block been falling when it was hit by the bullet?

Coefficient of Restitution:

The two types of collisions described thus far (inelastic and elastic) represent two ends of a spectrum. It would be better if we referred to them as PERFECTLY INELASTIC and PERFECTLY ELASTIC to emphasize this fact. Many collisions are very nearly perfect in either of these senses. When the collision lands somewhere in between these two extremes it is characterized by the Coefficient of Restitution - usually denoted with an 'e' - which describes the relative speeds of the objects before and after the collision. A perfectly elastic collision has an e = 1 telling us the difference between the speeds of the objects is the same before and after the collision. A perfectly inelastic collision has e = 0 because there is no difference between the speeds of the two objects stuck together afterwards.

For those of you who just have to know here is the formal definition of e, the coefficient of restitution.

2D Collisions:

Like all vector relationships in physics conservation of momentum applies in any and all directions. In the case where the collision is two dimensional (2D) or three dimensional (3D) the momentum in each direction is conserved independently.

Here is an example:

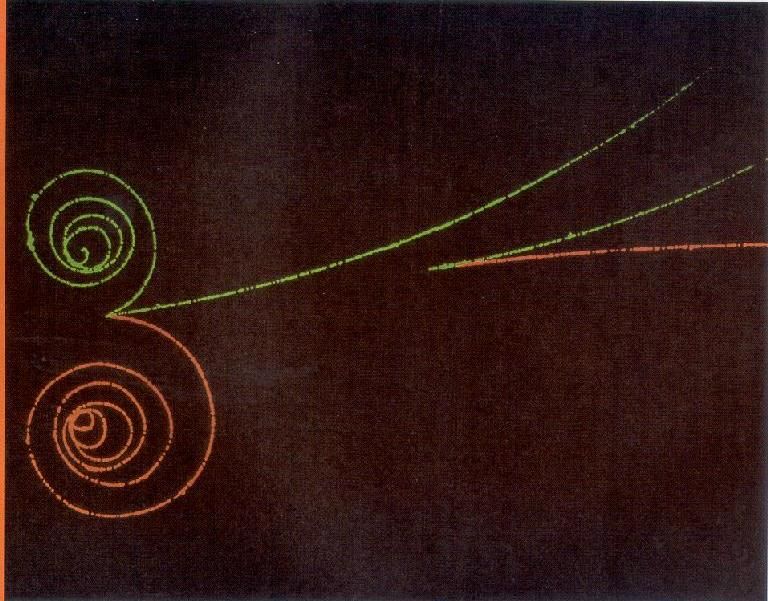
Consider the pair of particles on the right hand side of the image. We will talk more in PH212 about why their paths are curved but for now you can recognize that if I knew the speed of each particle I could determine the total momentum of the particles just to the right of the vertex. If momentum is conserved then where did this momentum come from? What we now understand is that there was a neutral particle that is invisible in this process that decayed into the two particles we see. Because this process is elastic and conserves momentum we can determine the mass of the invisible particle. Math is a mess but it works. In the early days of particle physics each vertex was analyzed by hand using conservation of momentum and energy. A lot of work.

Assignment: HW: Momentum Applications

Turn in the various (3) homework problems in this breadcrumb. For these problems please be attentive to our problem solving format and guidelines for different styles of problems.

Assignment: Reading

Momentum is a large topic but we will leave it at this point and move on to a final topic which is how all this Newton's Law stuff applies to making object spin (rotate). Read the Torque I breadcrumb.