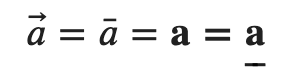NOTE: Because of all the images this page violates good web design principles and is quite long. Hang in there all the way to the end!
Vectors and Math:
Vectors are central to physics because it was realized long ago that some observed features of the world around us are best described by two characteristics: Their size, or magnitude, AND their direction. Eventually a mathematics of objects called vectors was developed that turns out to tremendously valuable in describing the physical universe. As a result we, as students of physics, need to become familiar with them and how to work with their unique mathematical properties. Don't expect this all to make instant sense but realize that it is an internally consistent system and you will get there with practice. In the begining it is always wise to sketch the vectors in a problem roughly to scale rather than approaching them as purely abstract mathematical creatures.
Vectors and Numbers 'Float':
An important idea that we take for granted with numbers is that the number is NOT attached to the thing that it describes. As an example if my bank balance is $14.23 I can use that number anywhere I want even though it describes something in the physical bank. $14.23 is the same number whether I'm using it to describe my bank balance or in my accounting software. This same idea applies to vectors though, because vectors are a newer concept, many students mentally attach them to an object or location in space. We'll talk more about this later but remember that a vector, like a number, is a description of something which doesn't exist at just one place.
Basic Concept of Vectors:
A vector is a mathematical object that represents two types of information. A vector has a magnitude AND a direction. As we begin this discussion it is helpful to think vectors as conceptually similar to arrows. Be careful, a vector is NOT an arrow but it is LIKE an arrow. An arrow has the same two characterisitics - a length (the magnitude) and a direction. We will start with vectors in 1D and work our way to vectors in 2D. The ideas here extend to 3D as well as other coordinate systems like polar and spherical. All vectors contain only these two items of information - a magnitude and a direction - even though it may take many terms to describe these two characteristics.
The University of Colorado Physics Education group has been building web based simulations for physics concepts for many years. Their simulations are based on research based studies of the challenges students have in physics classes (college and otherwise). I will link you to these simulations when it feels like they can be helpful. Feel free to explore the many others on their website.
1D Vectors:
Open the PhET vector tool linked above and choose the 'Explore 1D' option. You can use your cursor to pick up 3 vectors (a, b, and c) and place them on the page.
Notation Note: Notice the notation for the vectors a, b, and c in the PhET simulation. I can not easily reproduce the little arrow over the letter on a webpage. It is traditional to put a bar (without the arrow point) over the top of any symbol which we mean to be interpreted as a vector because it's quick and easy on a whiteboard but still not easy in text. In a textbook the tradition has been to make vectors boldface. In some classes the instructor will choose to underline vectors so it is not confused with the statistical symbol for the mean (average). You would be right to think this is a bit of a pain. Think of it as different mathematical dialects like the various dialects of English in this country. With a little practice you can learn to understand the word 'oil' as it is spoken in different parts of this country from oil to ahl to awl. Because web pages are text based I will try to use bold face to indicate symbols that are meant to indicate vectors.
Because they are limited to 1D (horizontal if that's what you picked) you can only choose whether they point left or right and you can make each one longer or shorter. Here is an example. I checked the values checkbox in the top right so it tells me how long each vector is. Again, there is a nomenclature to understand here. |a| is the magnitude (length) of the vector a. The most common use of version of this nomenclature is |a| = a where the magnitude of 'a' (the vector- boldface) is 'a' (the magnitude of 'a' - not boldface).

Directions and Signs:
If you click on the label for one of the vectors you will see the information box at the top displays the characteristics of the selected vector. I want to draw your attention to the bx or ax description of the vector. Shortly we will learn to call this the x component of the vector. You will notice that b is represented by -9 and a by +14. Because there are only two directions possible for a 1D vector we use signs to indicate whether the vector's direction is towards the + direction in the coordinate system or the - direction defined by the coordinate system. Please take a moment to recognize that the + direction of the x axis does NOT need to be to the right. This is why the process of labeling the + direction in your FBD from last week is important. The + direction is whatever direction you say it is!

Take Home: Signs (+/-) in vectors describe direction nothing more!!
Display the Sum:
If you now select the checkbox to show the sum you get this.
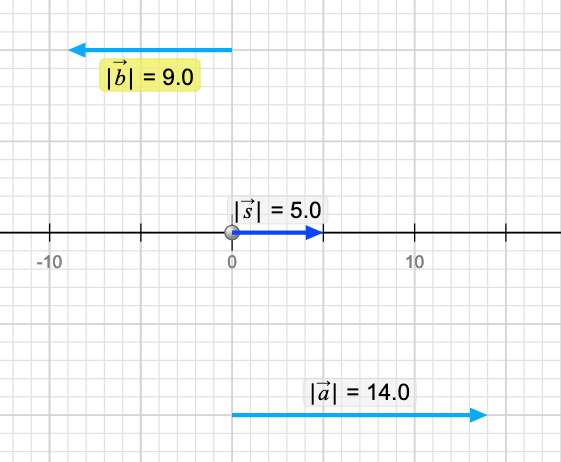
Mathematically this may seem totally obvious since 5 = 14 + (-9) and that is good. This is in fact how it works in 1D. s is called the resultant vector which is labeled s for 'sum' in this case. The notation for this is s = a + b! Notice that the result doesn't depend where you drag the two vectors on the page. Hopefully this reinforces the idea that vectors aren't attached to any particular place.
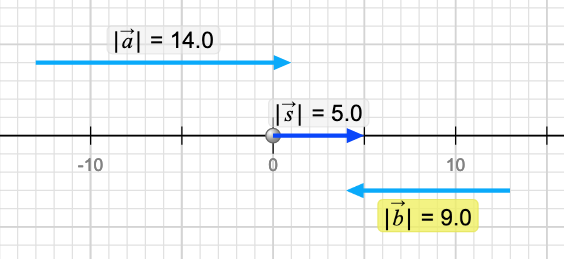
Graphical Addition of Vectors: Tip to Tail
It is equally important that you also develop a graphical picture of vector addition. The graphical method is called 'tip to tail' which instructs us to place the 'tail' of each successive vector in the sum on the 'tip' of the previous vector. The resulting vector representing the sum starts at the begining of the chain and ends at the end of the chain. I have offset the a vector by a bit to help with clarity but all three vectors lie on top of each other in some sense.
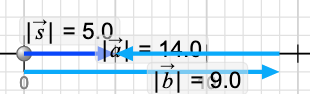
We can also see clearly that a + b = b + a which may be no surprise but is important to confirm.

Confirm for 3 Vectors:
Grab another vector c in the simulation and verify that it contributes to the sum exactly as you would expect from the previous discussion.
Magnitude Represents a Physical Quantity:
As was mentioned previously numbers without units are merely math. In all applications it is the units that give meaning to the numbers. In the world of vectors it is the magnitude of the vector which carries the units. Whether that is m, m/s, or N (Newtons) the magnitude has units associated with it.
Forces are Vectors!
Forces represent a physical quantity where both the magnitude of the force and it's direction are important. For this reason we use the mathematics of vectors to describe forces. Look back at the HW you did in the Newton's Laws: Applications and confirm that the calculations we did there match the rules for vector addition in 1D that we just explored.
Vector Properties:
I'm going to change to capital letters for my vectors so that it's a little more apparent when I'm making them bold. As part of the mathematics of vectors we have to be clear about what we mean by certain statements. These include what is 3A and what about -A?
-A:
Let's start with this one first because it is more intuitively comfortable for most folks. From our standard math the negative of a number allows us to satisfy this statement. 6 + (-6) = 0. If we follow the same logic what would we mean by A + (-A) = 0? Thinking about the graphical model of adding vectors (tip to tail) it is probably clear that if -A is just the same length as A but in the opposite (180o away) direction the equation can be satisfied. This the allows us to understand what we mean by A - B = A + (-B) = C.
Multiplication by a Scalar (Number):
So now, what do we mean by 3A? You might think of this as multiplication between numbers and vectors but it's helpful to remember that scalar multiplication (with numbers) is actually a short had for multiple addition. 3*7 = 7 + 7 + 7. If we are consistent (always helpful with math) then 3A = A + A + A which is just a vector 3 times as long as A and still pointing in the same direction. This idea will become important when we get to unit vectors and components in 2D vectors.
Assignment: HW: 1D Vectors
There is no HW for this section. Our HW will all take place in the 2D Vector discussion.
Assignment: Reading
Explore the Vectors 2D breadcrumb to extend what we've done here to 2D.