Angular Motion:

All that we have done up to now has been entirely focused on the translational motion of some object. In this context translational means the motion of an object (more specifically it's center of mass) from one location to another. Along the way we have treated all objects like small point like objects. As you are well aware the motion of real objects is much more complex.

It is worth noting at this point that this process of starting by simplifying our system and trying to understand the most basic setting before moving on to more complex systems is the foundation of the scientific approach to understanding. This is partly because this process has historically been quite successful at moving our understanding forward. It is important to acknowledge that there are cases where this process (sometimes described as a reductionist approach) can be ineffective. For the processes we are exploring in this class it is a very effective process.

In keeping with the process described we are now going to consider an object which is not translating but is rotating around some axis. Rotation and translation are distinctly different processes and need different symbols/language.

Angular Labels:

You will not be surprised that we will use angles to describe the angular position of an object. If that angular position changes then it must be moving angularly (we need a symbol for angular velocity) and if that angular velocity is changing that would represent an acceleration for which we also need a symbol. These angular variables are all related in the same way that our linear variables are (through derivatives - slopes - and integrals - areas - on plots). Here is a summary of these concepts.

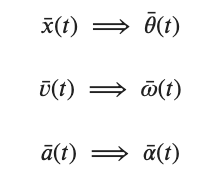
Yes, they are vectors although we won't worry about that for now. θ (theta) you are familiar with. ω (omega - not 'w'!) is the symbol for angular velocity. α (alpha) is the angular acceleration. The convention is that we use greek symbols for angular variables and standard letters for linear (translational) variables.

Units:

Because we will want to related the tangential (linear) velocities of points on a rotating object we measure angles in radians to facilitate that process. As a result θ has units of radians, ω has units of radians/s (rad/s), and α has units of radians/s/s (rad/s²). The angular variables are related to each other in the same way as their linear equivalents.

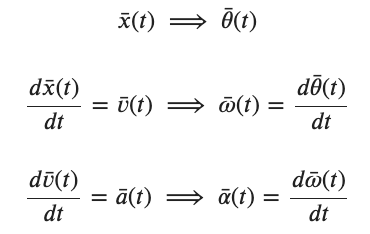
Nor will you be surprised that, because of the equivalence between the two, that our kinematic relationships that we derived from Newton's Laws also apply to angular variables.

We will explore how Newton's 2nd Law transforms for rotational dynamics next time. Before we do so we need to connect a few aspects of angular motion and linear motion in the context of rotating objects.

Angular Velocity, Period, and Frequency:

Particularly for objects that rotate at a constant rate we describe the time it takes for the object to complete one rotation as the period. In physics we usually indicate the period with the symbol T and report the period in seconds (s). When the period gets short it can be easier to describe the number of cycles the rotation completed in each second. We call this the frequency and use the symbol f. Since T is s/cycle and f is cycles/s it must be that T = 1/f and f = 1/T.

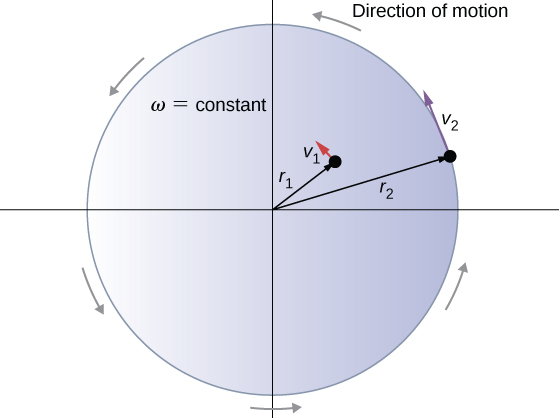
If we now consider an object that is rotating we will notice the following relationships the angular variables and the tangential velocity of a point on the edge. In this graphic S is the arc length (distance) that the edge has traveled in some time. θ = S/r is the definition of the angle θ in radians. The velocity vector describing the motion of a point on the edge is tangential to the path of that point and, as we saw in circular motion, is always changing direction.

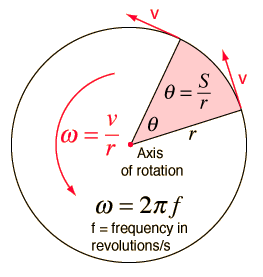
Thinking about the distance a point on the edge travels in some period of time we can say....

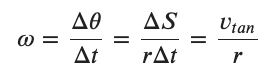
We can apply this idea even to objects traveling along a circular path like the earth going around the sun. We can articulate the angular velocity of the position of the earth along it's path relative to it's tangential velocity.

From a similar perspective the object turns through and angle of 2π radians in one revolution which takes T seconds (1 period) which leads us to....

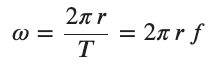
It is important to note that different points on the object are a different radii from the axis of rotation and hence have different tangential velocities even though they have a common angular velocity.

The tangential and angular variables that describe a particular point on a rotating object are related by these expressions....

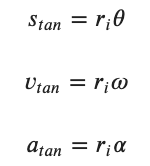
This relationship is at the root of this cartoon from Bill Watterson (Calvin and Hobbes).

Thanks to Bill Watterson for his support of physics

Now that we've got all these relationships out on the table we can examine the forces that are needed to make an object rotate. Your personal learning experience around the dynamics of rotating objects will be informed by your experiences with merry-go-'rounds so think about that before next time.

Angular Variables:

What is the angular velocity of the earth around the sun? What is the tangential velocity of the earth along it's path around the sun? The distance from the sun is 1.5 10¹¹ m.

Angular Variables:

A CD (ancient digital music tech) needs a constant tangential velocity to deliver the data at the proper rate to the player. This velocity is 1.3 m/s. The outer edge has a radius of 6 cm and the inner most track has a radius of 1.5 cm. You may have noticed that the CD spins at a different rate when playing different songs. The first track is on the inner most part of the CD and the last track is near the edge. What is the angular velocity of the CD at each of these locations?

Angular Variables:

Engineering components are often tested in centrifuges. One such centrifuge has an angular acceleration α = .192 rad/s². Assuming it starts from rest what is the angular velocity (ω) of the centrifuge after 120 s and how many revolutions has it completed (find θ and then convert to revolutions). Your tools are the angular versions of the kinematic equations.

Assignment: HW: Angular Variables

Turn in the various (3) homework problems in this breadcrumb. For these problems please use the problem solving format described in the Concepts breadcrumb.

Assignment: Reading

Go on to the Torque breadcrumb to explore how Newton's 2nd Law connects to angular motion.