Example Settings:
Follow along on the problem solving frame for Circular Motion which is really just an update to the standard Newton's Law frame.
Mass on a string on a horizontal frictionless table:
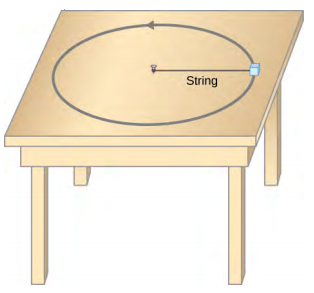
As we noted previously the image below is a reasonable representation of the forces acting on the mass. Now we need to choose a coordinate system, check for components, build the table of forces, and write Newton's 2nd Law. Piece 'o cake eh?
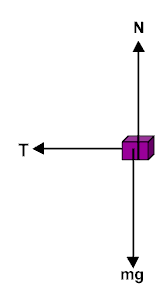
Here's what that looks like. NOTE: I intentionally chose the radial axis first and assigned (+) towards the center of the circle. No components to worry about since all the forces are already along the axes - sweet!
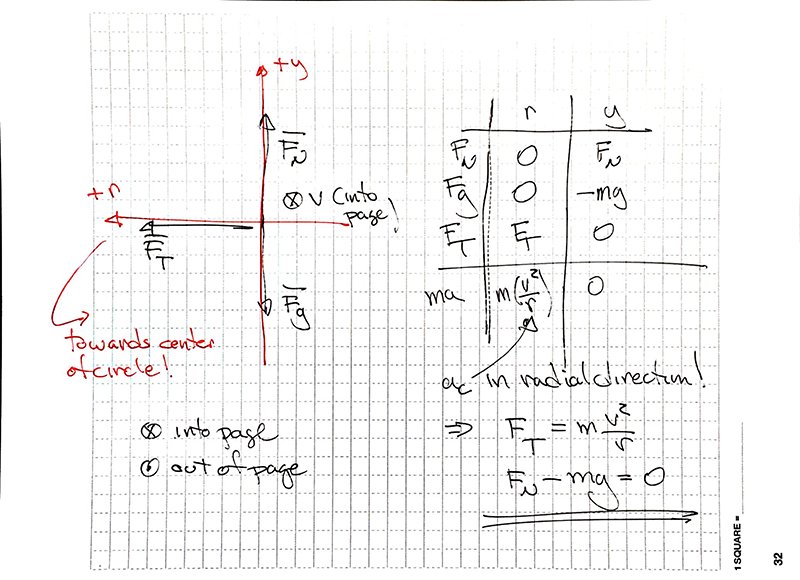
Another Note:
I think it is wise to always indicate the direction of motion of the object someplace near my freebody diagram. The velocity is NOT a force but it is relevant to possible frictional forces or other features of the problem. In this case the mass in the picture is moving 'into' the page (away from me). To illustrate this the usual convention is, when you are looking at the tail of an arrow going away from you, to show the fletching (feathers) on the tail of the arrow. This is what the X is meant to signify. I know, there are usually 3 feathers not 4 but it's an abstract idea and an X is quicker and easier than three lines in a peace sign. You might well ask how you would indicate an arrow coming toward you. As shown on the sketch above we usually indicate 'coming toward you out of the page' with the point representing the bright tip if the arrow. The circle around the dot helps distinguish the dot from other possible specks on the page.
What would be different about this version of the problem?
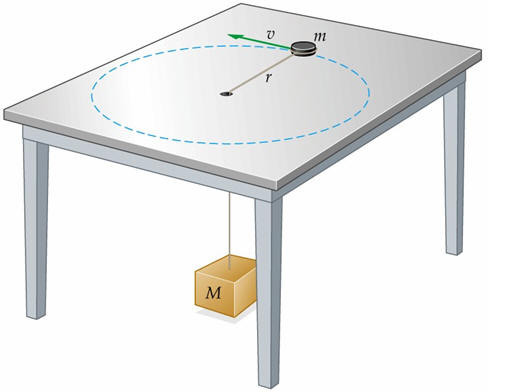
Hopefully you notice that the weight of the hanging mass (if it's not moving) is the same as the tension in the string which you just explored in the previous setting.
What replaces the tension in the string if the mass is a car going around a corner?
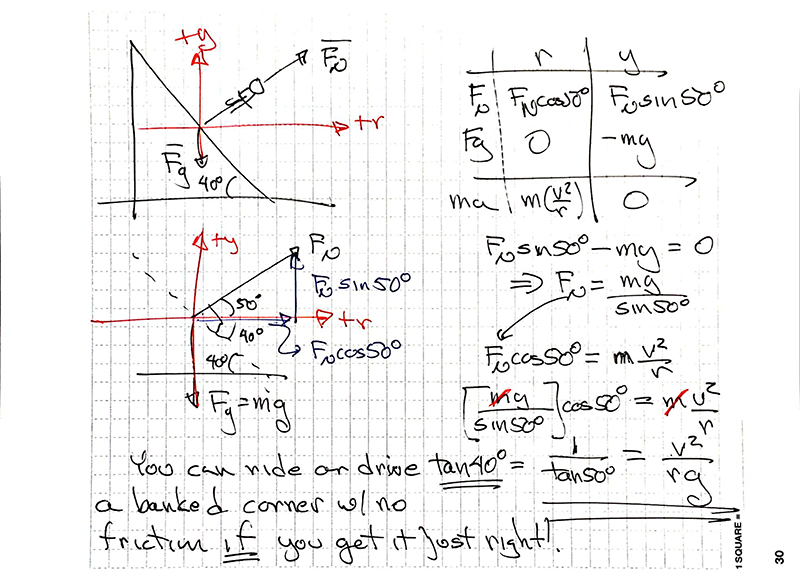
Banked Corner:
We are all very used to banked corners and have pretty good intuition about them. Let's see how that works out. Here is an image of bikers (fixed gear) on a velodrome track. The angle of the track is quite steep which we will take to be 40o and we will start by assuming NO friction.

thanks to Jocelyn Wong for the image
Make a sketch, determine forces, choose coordinate system, do components, build table, write Newton's 2nd Law. Then think about what the question is.
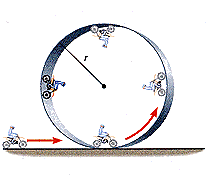
Vertical Circle:
The underlying question here is how fast to you have to be going at the top of the arc to 'make it over the top' without falling off. You will find that many people start with the idea that as long as you get to the top with v = 0 you can make it safely around the loop. Freebody diagram at each of the 4 locations......choose coordinate system at each point......
Here's a version of the different freebody diagrams...
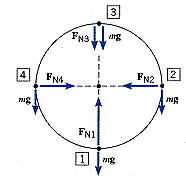
Failure to Loop:
A common feature of interest is to ask how fast the biker needs to be going to complete the loop without falling off. Where in the loop is the moment of truth? Can you be stopped at this point? What will it feel like if you're right at the hairy edge? What does this mean about the normal force (FN3)? Can you determine the speed vmin that keeps me from falling off at the top? What does it mean that the mass is not part of the solution?
There used to be a rolling barrel in Lithia Park in Ashland that I have experimented with to see if I could make it over the top but no luck!
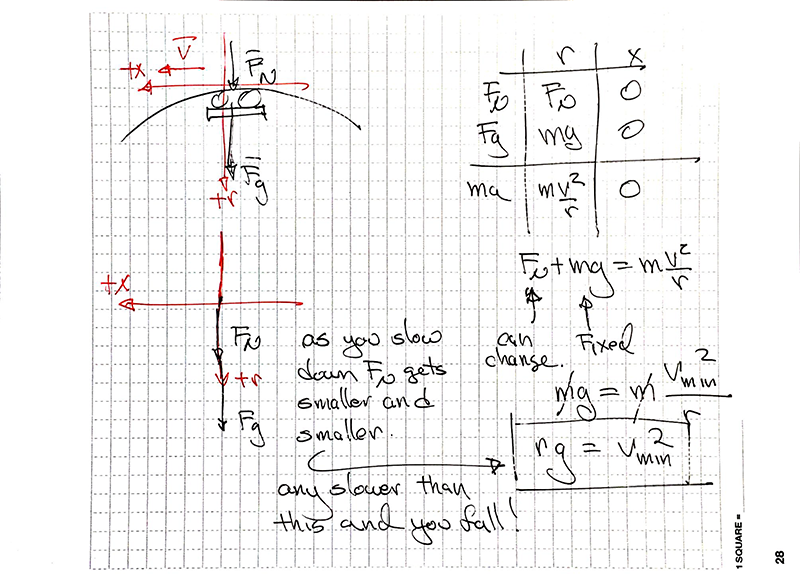
What does it mean that vmin does not depend on the mass? We will see this sort of behavior from time to time in physics and it is important to recognize what the absence of mass dependence implies.
Actual Speed vs Constant Speed:
Is it reasonable to imagine that the biker is maintaining constant speed through the loop given the freebody diagrams? For now we will assume that the speed is constant until we have some more effective tools for figuring out what the speed actually is at each location. Myth Busters did an episode a exploring the reality of loop the loops.
Activity: Why is it difficult to determine the acceleration of the biker/mass as it moves along the loop? Perhaps it would be more appropriate to say the integrating the acceleration to get the velocity at different points along the loop is the real challenge?
Banked Corner with Friction:
Here are two images of objects moving in circles on banked corners.You are undoubtedly aware from your winter driving experiences that there are two possible undesirable outcomes to driving on banked corners when friction is low. If you go too slow you can slide down to the bottom of the corner and if you go too fast you 'blow out' the top.
Make a sketch, determine forces, choose coordinate system, do components, build table, write Newton's 2nd Law. Then think about what the question is.
Activity: Consult with your group about your Freebody Diagram. Be sure to discuss the direction of the frictional force (two possibilities -- why in each case) and the direction of the 'radial' axis that you chose.

and....

Airplanes flying in circles have very similar freebody diagrams.
Summary:
Perhaps you begin to understand why I keep beating you up about the freebody diagrams and explicit choices of coordinate systems. Every force on your freebody diagram, except the force we call gravity, requires an explicit contact with your system or object of interest. You can 'solve' the problem with any choice of coordinate axes but some versions are much less effort than others. Care and thought at the begining is critical.
While it may seem that this exploration of circular motion is limited to circles and constant speed it in fact applies to any motion along a non-linear path even while changing speed. What calculus teaches us is that if I take a narrow enough window in time (like instantaneous) there is a definite radius of curvature at that point on the path. Over that same short period of time we can take the speed to be constant. After that ....it's just math!
HW: Circular Motion
A conical pendulum is a ball on a string which is swinging in a horizontal circle. The angle between the string and the vertical direction is constant. Consider such a pendulum with a 20 kg ball on the end of a 3 m long string which makes an angle of 5o with the vertical as it swings. Find the tension in the string and the period of its motion.
HW: Circular Motion
You are needed to design a highway curve for traffic traveling at a constant 60 km/h. Due to constraints of the landscape the radius of the curve must be 150 m. What is the appropriate bank angle of the curve so there will be no problems on an icy (frictionless) day? If you design the curve as a flat curve what is the minimum coefficient of (static or kinetic?) friction needed?
HW: Circular Motion
An airplane is flying in a horizontal circle at 480 km/h. The wings are tilted at 40o with respect to the horizontal. Assume that the lift force of the wings is directed perpendicular to the wings. What is the radius of the circle in which the airplane is flying?
HW: Circular Motion
Assume for a moment that you are traveling around a loop in the vertical plane at a constant velocity of 20 m/s. What is the function that describes the radius of the loop at each point (a function of θ makes a lot of sense) so that the normal force you experience is a constant 2 g's? (Give this a try - it does have an answer and its not as bad as you might think:) There's a picture and a discussion of this problem in a Gizmodo article that you may find interesting.
Assignment: HW: Circular Motion
Turn in the various (4) homework problems in this breadcrumb. For these problems please be attentive to our problem solving format and guidelines for different styles of problems.
Assignment: Reading
Next we move on to another way of exploring physical settings from the perspective of energy. Start with the Work/Energy breadcrumb
