Newton's Laws
Last time we developed a process for creating freebody diagrams and explored the underlying ideas for Newton's 1st Law. In this breadcrumb we will move on to Newton's 2nd Law which allows us to take a more calculational approach to the forces on our freebody diagram. Newton's 3rd Law will also be introduced.
What if the forces are not balanced?
If you're hanging in there with this train of thought then the next question is how many forces are acting on a ball AFTER you drop it? Draw your freeebody diagram and be prepared to discuss. Most people are pretty comfortable with their answer on this one (and they're correct). Now watch the first 45 s of this Veritasium video and decide which prediction makes the most sense to you. Made your choice?.....then watch the tests for the next minute of video.
Before you go on to 'get the answer' stop and reflect on what could be wrong with the thinking of those whose predictions were wrong. Let's be clear -- those who predicted correctly don't have very coherent explanations for their predictions either. After you've thought about it then you will at least get some benefit from watching the video through to the end.
...which leads us to the next set of thoughts.
Proportional Reasoning:
Before we head off to this next activity let's talk about proportional reasoning. It's one of the ideas/skills that others imagine you some catch like a cold from being in a physics class. Definitely not that easy to catch!
What is the proportional relationship between the number of hours you work and the size of your paycheck? Unless your life is pretty unusual the more you work the bigger your paycheck. That is considered a direct proportion. Both quantities move in the same direction. x is proportional to y.
As you climb higher up the mountain how does the available oxygen change? How are the elevation and the oxygen concentration related? Perhaps you have heard or experienced that the greater the elevation the less oxygen is available for your body. This is called an inverse proportion. When one quantity increases the other decreases. x is proportional to 1/y.
Tortured Example: Proportional Reasoning with 3 Quantities
I am NOT asserting that the following is true but only that it is one way you might think about it. Consider $$, time, and happiness. To figure out how they MIGHT all be related we have to hold one quantity constant and consider how the other two are related. If we keep the $$ we earn constant many would suggest that spending less time making that $$ will lead to more happiness. Happiness (H) and time spent working are inversely proportional. H proportional to 1/time. If I want to keep my happiness constant then my $$ need to go up as my time worked goes up. This suggests $$ and time are directly proportional. $$ proportional to time. Finally, if I keep the time I spend working constant and increase in the $$ I earn will probably increase my happiness. Happiness and $$ are directly proportional.
So how do I write a mathematical relationship that reflects the same relationships using the symbols H, $$, and time? Here are some possibilities:
H = $$ * time; H = time/$$; H = $$/time; 1/H = $$*time
Which of these expresses the same proportional relationships? H=$$/time
Activity: We will probably take a moment for you to explore in groups how you decided which of these expressions correctly represented the stated proportionalities.
Back to Forces.....
A Thought Experiment (Einstein called these gedankenexperiments):
We take you, a puppy, and a pygmy elephant up in the Space X rocket (for a modest fee) and outfit everyone with space suits. We go way out into space between the earth and Mars where gravity is very small (are you sure?). We lay you down on a platform on the outside of the spaceship - velcro may be involved.
I 'set' the puppy on 'top' of you...what does this 'feel' like? I 'set' the pygmy elephant on 'top' of you ....what does this feel like? What does this have to do with our ideas of 'weightlessness'?
Next we go to opposite ends of the space ship and stand outside against walls facing each other at 50 m. Now I 'throw' the puppy at you with a velocity of 5 m/s. Imagine what this feels like when the puppy hits you (you will actually catch them gently but you can imagine..) Is this different than the previous experiment? Is the puppy still weightless?
If I 'throw' the puppy slower will it take more or less force to stop it safely?
Now I 'throw' the pygmy elephant at you with the same velocity of 5 m/s. Does this feel different than the puppy when the elephant hits you? Why? What is it that the pygmy elephant has more of than the puppy? Can't be weight since we have demonstrated that both are 'weightless'. Maybe not?
If I 'throw' the pygmy elephant slower will it take more or less force to stop it safely? Does it take more or less force to stop the elephant or the puppy?
Do you see that stopping the puppy or the elephant involves changing their velocity which means they are accelerating. Same change in velocity in the same time requires the same a, a = Δv/Δt.
We now have three characteristics that seem to be related. The force that we apply to an object, the acceleration that the force produces, and something about how much 'stuff' the object has. We'll clarify this 'stuff' idea immediately
Stuff (mass):
Something suggested by this thought experiment is that there is an intrinsic characteristic of all objects which doesn't require gravity to exist. We call this characteristic mass and it is a measure of 'stuffness'. Heavy things have a lot of it and light things only a little. Mass is measured in kg (kilograms). Until recently we used a reference kilogram stored in Saint-Could France to determine what a kg is. Just for the record the reference kg seems to be losing weight which is aggravating. [this link to a Vox article describes the new definition of the kg in terms of the Planck constant. I have no idea how long the link will last so let me know if it expires:)]
Just a warning, in spite of our desire to connect lbs (pounds) and kg they are NOT the same thing. Pounds describe forces and kg describe mass and they are very different concepts. We'll worry later why they are used interchangably on this planet.
Proportional Reasoning about Force, Mass, Acceleration:
Using the same methodology we did before we will hold one variable constant and consider how the other two connect with each other.
Keep Force Constant; How are Mass and Acceleration Related?
Hopefully your experience is that if you push on something with the same force you get different effects depending on the mass of the object. Be careful, much of our intuition is shakey because we rarely experience objects with a single force. The closest we can usually get is a situation where friction is a small factor. Under these circumstances does your experience suggest that the same force on a bigger mass leads to bigger or smaller acceleration? As the mass increases the acceleration decreases for a constant force => inverse proportion between mass and acceleration.
Keep Mass Constant; How are Force and Acceleration Related?
If you push harder on the same object do you expect more or less acceleration? I would imagine that you are pretty comfortable that your experiences (experiments) tell you that more force gives more acceleration when the mass stays the same. As the forces increases the acceleration increases for a constant mass => direct proportion between force and acceleration.
Keep Acceleration Constant; How are Force and Mass Related?
This is actually a bit harder to visualize because we rarely have direct experiences where we try to get different objects to have the same acceleration. Here's a possible situation. Imagine you want to accelerate over some distance like 10 m. That will take some particular amount of time. If you crosss the 10 m in the same amount of time while speeding up continuously that suggests you have the same acceleration due to the forces from your legs. Now, compare the force you need to generate to keep the acceleration the same when you are carrying a 12 kg (25 lb) medicine ball to the force needed with no medicine ball. Your experience probably tells you that it will take more 'effort' (force) to maintain the same acceleration with more mass involved. More mass requires more force to yield the same accelaration => direct proportion between force and mass
F = m * a; F = m/a; F = a/m; 1/F = m*a
Which of these expressions reflects the relationships we believe we have experienced? F = m*a It's a fair question whether there are other factors that should be considered. Extensive experimentation indicates that this is all there is.
Net Force: Fnet:
We use the term 'net force' or Fnet to describe the collective effect of all forces acting on an object. It is important to understand that Fnet is a description of the collective effect of forces and NOT a separate force on it's own. Fnetshould not show up as a force on your freebody diagram.
Newton's 2nd Law
If we pull all of this together we get the following mathematical statement of Newton's 2nd Law.
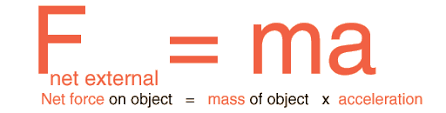

You can read and understand this in any language you are likely to meet. If you are an engineering student this is the single most used mathematical expression for your first two years of school and possibly longer. Note that it describes the acceleration produced by the NET FORCE which is the collective equivalent of ALL the forces acting on an object.
Newton's 2nd Law: Units
This is a good place to start the process of building units. Mass is measured in kg as compared to the reference kg in France (recently changed!) and accelerations are measured in (m/s)/s = m/s2. To be clear, a = Δv/Δt which has units of (m/s)/s. This means the units in which we measure force are kg-m/s2. Because this combination of units comes up so often we give it a name. A Newton (N) = kg-m/s2. Expressed in words 1 N is the force that will cause a 1 kg mass to increase it's speed by 1 m/s every s. In the Imperial/British system of units this is more confusing and we will save that for a later discussion.
Newton (N) = kg-m/s2
Connection to Newton's 1st Law:
You might note that if Fnet = 0 Newton's 2nd Law says that m*a = 0 which requires that a = 0 because m is not 0. If a = 0 then the object does NOT change velocity which is what the 1st Law says. If the 2nd Law is equivalent to the 1st Law why do we need the 1st Law you might ask? The 1st Law is how we test to see if Newton's 2nd Law will be valid. Philosophically that's why the 1st Law exists and not so much because it says something different than the 2nd Law.
Force of Gravity:
Because almost all problem settings that we address this term will be in an environment where there is gravity it seems like this is a good time to talk about this ubiquitous force. This is a semi-magical force that we will treat very casually. Newton and Cavendish figured out a description but explaining why gravity exists is more philosophical and complex. For now here's the descriptive rule:
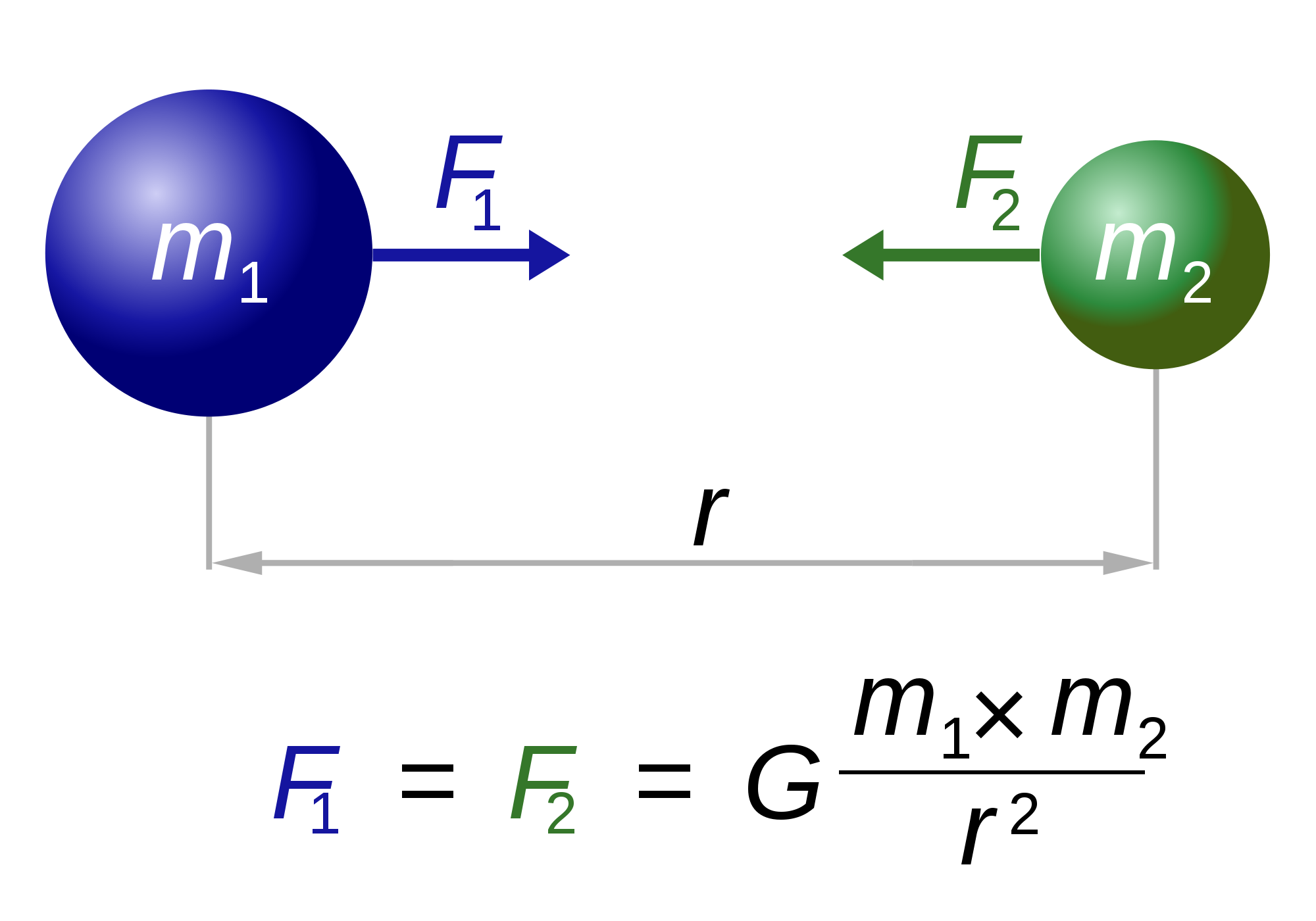
G is the gravitational constant (6.674×10−11 N · (m/kg)2);
m1 and m2 are the two masses which are pulling on each other. Cavendish originally figured this out using naval cannon balls which create pretty subtle gravitational forces. r is the distance between the centers of the objects. For all objects on the surface of the earth three of the four terms in this expression are essentially constant. G, rearth, and mearth.
We can precalculate all of the terms except the mass of the object on the surface of the earth that is experiencing the force of gravity. When we do so get a constant we call g = 9.8 (m/s)/s....or for this class we'll call it 10 m/s2. This is why we often casually say ... Fg = mobject.g
Fg = mobject.g
Newton's Law Frame: Problem Solving
Examples:
In the begining it will feel like a whole lot of overkill to do all of these steps. On the other hand, what we are practicing is a structured approach to problems involving forces that keeps on being successful when we get to more and more challenging problems.
A 2 kg book sitting on a table:
A 2 kg falling book (no air drag):
Same book with a 5 N force due to air drag:
sorry -- the video is a bit breathy -- I'll move the microphone in the future.
Elevators:
Make a freebody diagram for yourself standing in an elevator. Does this freebody diagram ever change as the elevator stops and starts?
Let's do some conceptual reasoning from Newton's 2nd Law. The direction of the net force must be the same direction as the acceleration. For this setting this is essentially a question about which force is bigger on our freebody diagram. Decide first which direction you think the acceleration is pointing (which is the same as the change in the velocity) and then you will know which force must be bigger. Does Fg ever change?
- i) The elevator is at rest.
- ii) The elevator is moving upward at increasing speed.
- iii) The elevator is moving upward at decreasing speed.
- iv) The elevator is moving upward at constant speed.
- v) The elevator is moving downward at decreasing speed.
- vi) The elevator is moving downward at constant speed
Activity: Discuss these 6 settings with your group. Identify which force on your freebody diagram is bigger or are they equal.
Normal Force: FN
Another language clarification seems warranted at this point. When two rigid objects like a box and the floor make contact there is a force between them. We could label it the Ffloor which would be perfectly reasonable. It also has the characteristic that it pushes on the box in a direction which is perpendicular to the floor. If the floor is sloped this force continues to push perpendicular to the floor and NOT straight up. In math the 'normal' direction is a direction perpendicular to a surface. For this reason the contact forces between objects are often labeled as normal forces FN . This can get confusing as there may be multiple objects in contact with your object of interest.
Calculationally:
Each of these questions below only changes after step 7 in the problem solving frame. Just go to that point and consider your numerical values.
Assume your mass is 60 kg -- what is the normal force (FN) acting on your feet when the elevator is at rest?
You push the button to go up to the 6th floor. What can you say about the relative magnitude of the forces acting on you? Will this relationship hold throughout the trip to the 6th floor? Where will it change and how?
If the initial acceleration on your way to the 6th floor is 1.6 m/s2 what is the normal force now? What is the normal force as you ride along between floors at a constant speed?
When you arrive at the 6th floor you have a momentary sense of being 20% lighter than normal. What force is this that has changed? What is the normal force now and what is your acceleration?
HW: Newton's Laws: Applications
A 700 kg pallet of equipment is hanging from the 25 m long cable of a crane. What is the tension in the cable under each of the following circumstances? Be sure to do a freebody diagram (force picture).
- i) The pallet is stationary.
- ii) The pallet is moving consistently upward at 5 m/s
- iii) The pallet is accelerating upward at 5 m/s2
- iv) The pallet is accelerating downward at 2 m/s2
[7kN, 7 kN, 10.5 kN, 5.6 kN]
HW: Newton's Laws: Applications
Space sailing is a possible (low acceleration) means of moving masses around in space using the force generated by sunlight pushing on a 'sail'. Digging up my old notes I find that for a good sized sail NASA predicts one could generate a total force on the sail of 8 N. (just 8!) At the same time, estimates of the mass of the sail and its payload are in the 3800 kg range for a small payload. Ignoring the effect of the sun's gravity for the moment what is the acceleration of this space object? Don't forget to do a freebody diagram.
[2mm/s/s]
HW: Newton's Laws: Applications
A group of folks are riding in a hot air balloon 60 m above the ground. The total mass of the balloon and its occupants is 300 kg. The balloon is stationary in the air due to the upward buoyant force of the hot air. Do a freebody diagram of the balloon. If the buoyant force remains constant what mass of sand must be thrown overboard so that the balloon acquires an upward acceleration of 0.5 m/s2?
[14 kg]
Thing 1 and Thing 2: Newton's 3rd Law
We can certainly get very sophisticated about our language but in the end it boils down to identifying thing 1 and thing 2 -- what two objects are interacting that lead to the force in our freebody diagram? Can you think of any force that is NOT the interaction between just 2 objects?
The core observation is that each of the two objects that interact experiences a force. The relationship between these two forces is expressed in Newton's 3rd Law. For now let's just take the 3rd Law to say that there are two things that interact and each experiences a force. We'll worry more about this when we look at Newton's Laws in 2D.
Here is the labeling we will use to capture the two things: Fthing 1 -> thing 2. Be careful, we're asking about the forces on the object (thing 2) for which we are drawing the freebody diagram! Here is how the 3rd Law is framed more formally. The minus sign just tells us that the forces are in opposite directions.
Fthing 1 -> thing 2 = - Fthing 2 -> thing 1
HW: Newton's Laws: Applications
(Calc) The location of a 100 g particle is given by the expression
y= 8 t3 - 3t + 14 (in meters).
What is the net force on the particle at t = 2.0 s? Think about the mathematical relationship between position and acceleration from MTH 251!
[9.6 N]
Assignment: HW: Newton's Laws: Applications
Turn in the various (4) homework problems in this breadcrumb. For these problems please use the problem solving format described in the Concepts breadcrumb.
Assignment: Reading
Next week Monday is the MLK holiday so we only meet on Wednesday. Explore the Vectors breadcrumb where we will dig into the mathematical objects called vectors. This includes 2D vectors represented by components and unit vectors. Lots of abstract math!
