Newton's Laws: 2D and up
We have established that forces are an interaction of some kind between two objects. We have explored the underlying experiences and concepts that lead to Newton's 1st and 2nd Laws (Fnet = 0, Fnet = ma). In this section we will complete the trifecta (Newton's 3rd) and then explore richer applications of all of these in more than one dimension. We will also introduce a simplified model for friction that will be useful in a variety of contexts. Onwards....
Thing 1 and Thing 2: Newton's 3rd Law
We started this discussion when we developed our initial understanding of Newton's Laws. We will continue to practice this idea of thing 1 and thing 2 and the pair of forces that are the result of the interaction between them. As usual lets start with some examples and here is a reminder of the formal statement of Newton's 3rd Law.
Fthing 1 -> thing 2 = - Fthing 2 -> thing 1
Create a quick freebody diagram for the following setting: a book sitting on a table
 normal force
normal force
 gravity
gravity
There are 2 (perhaps 3?) forces acting on the book. What are the 3rd Law forces for each the forces in this problem? On what do they act and in what direction?
Caution:
Somewhere along the way we have (mostly) internalized the sense that Newton's 3rd Law is about equal and opposite forces which leads us to think of Fnormal and Fgravity (in the case of the book) as 3rd Law pairs when they are NOT. This may seem like much ado about nothing but clarity about 3rd Law pairs becomes critical when we are analyzing a complex stack of objects in some setting. It also helps us determine which forces act in which direction on which object. We will see some of this a little later when we consider multiple objects with friction.
a car driving down the road at high speed
 air drag
air drag
 friction?
friction?
There are 2 (perhaps 3?) additional forces acting on the car. What are the 3rd Law forces for each the forces in this problem? On what do they act and in what direction?
A book sitting on a ramp without moving? Tbink it through.
Note: 3rd law pairs can NEVER act on the same object!!
Classic 2D 'Ramp' Problem: Prezi
It's all about the process and not about clever insights. This Prezi explores the sequential steps of the Newton's Law problem solving frame. As always it starts with a freebody diagram, then a choice of coordinate system, determine components if needed, apply Newton's 2nd along each axis, solve, and check. While there is friction in this example we will set friction aside for today and look at problems without friction.
While there is friction in this example we will set friction aside for today and look at problems without friction.
Here is a simplified version of the same problem for us to actually solve. Note that we will use rotated coordinates in this particular problem and discuss the reasons for doing so.
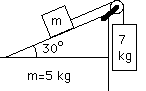
Two objects but No Ramp:
In a more complex problem take each object individually and make a freebody diagram. Use Newton's 3rd Law to connect forces on the related freebody diagrams. For now we will consider this without friction.
Physics Ropes:
Ropes, or things like ropes, are a feature of many physical settings. When a rope is shown or described in a physics problem it is assumed to be an 'idealized rope' which is available from the 'Catalog of Ideal Physics Equipment' (finally somebody has built the catalog!). An ideal physics rope is weightless, unstretchable (inextensible), perfectly flexible, and infinitely strong. Cool stuff if you can get it. Real ropes are more like very strong springs with mass and that will wait for another day!
It is a property of all ropes, ideal or otherwise, that they can only pull and never push. This may be obvious but recognize that this imposes some expectations on your freebody diagrams.
Tension 'in a Rope':
We often talk about the tension in a rope or cable but it's not initially clear how that tension shows up on our freebody diagram. The tension is a rope is defined to be the force that is applied to it, and that it applies to the object it touches, at one end. If you were to 'cut through' a rope the tension at that location is the force needed to keep the ends stationary relative to each other. For ideal physics ropes the tension is the same everywhere in the rope. In real ropes and cables with mass the tension varies throughout the rope.
Objects connected by a rope:

Similar but on a Ramp:
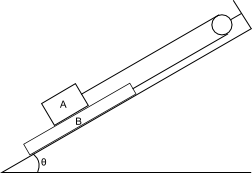
Newton's Laws: 2D
Take the weight of the hanging object (a traffic light is a possibility) to be 850 N. Find all of the tensions. This will take a couple of freebody diagrams but at least this is a static (not moving) setting!
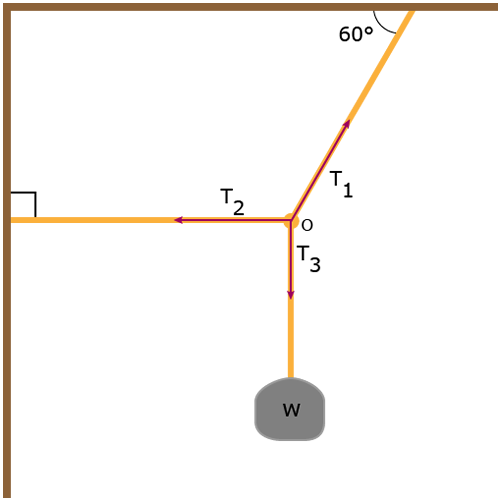
[982 N, 490 N, 850 N]
Newton's Laws: 2D
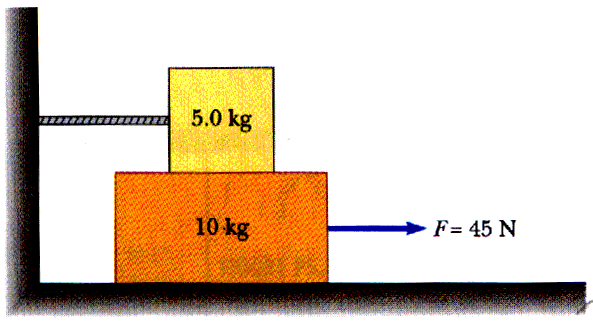
In the following image take m1 = 12 kg and m2 = 4 kg. The force F from the physics student is 140 N. HOWEVER instead of being horizontal the force F is directed downwards at 30o relative to the horizontal. The table remains flat. Find the collective acceleration of the masses in the absence of friction. Does it matter which side you push from? The consider the contact force (f) between the masses. What is this force and is it the same when F is applied from the left or the right?
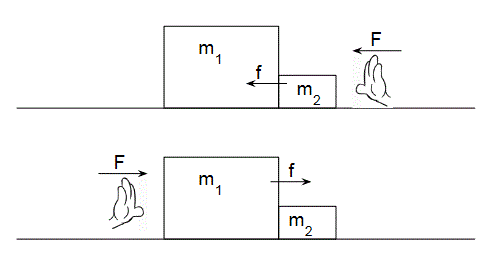
[7.6 m/s2, 30 N, 91 N]
Newton's Laws: 2D
A search and rescue person is working their way backward down a slippery (frictionless) ramp that is inclined at 18 degrees. He is using a rope to maintain stability and keep his body perpendicular to the surface. The weight of the rescue person is 650 N. What are the magnitudes of all the forces on your freebody diagram?
[650 N, 618 N, 201 N]
Newton's Laws: 2D
The ramp is frictionless. What happens? A traditional physics problem would direct your attention to figuring out the acceleration of the block(s). At the very least you should do that but as a science student is that all you can figure out?
[64.5 N, 43.3 N, 7.9 m/s2]
Assignment: HW: Newton's Laws: 2D
Turn in the various (4) homework problems in this breadcrumb. For these problems please be attentive to our problem solving format and guidelines for different styles of problems.
Assignment: Reading
Now we get to add a simplified model for friction to all of these problem settings. See Newton's 2D II breadcrumbs for an intoduction to the basic model for friction!