Friction:
So how does friction work? Perhaps a more interesting question is what does it mean to understand how some process works? (Discussion)
The bottom line is that friction is very complex and situational. In general we create approximate models that work in the range that we are interested in. Examples include rolling resistance and air drag in vehicles.
In case we ever want to dig deeper here is a very useful overview of a physics view of friction. In a more specific case you can consider this paper on the details of how our fingers experience/detect friction.
Direction of the frictional force:
I agree this may seem obvious but I think I can quickly convince you that there are times when you have to be careful. Consider the freebody diagram of a person accelerating down a track. If there were no friction on the feet there would be no running down the track. So which direction is the frictional force pointing on your freebody diagramn of the person? Does this fit with the usual statement that friction always opposes the motion of the object?
The Splinter Model:
This technique does sometimes make us all cringe but it is also true that I have never seen it fail. For whatever reason we have too many unfortunate experiences with splinters. Imagine you are the object of interest in your freebody diagram and the source of the frictional force is a splintery board. Which way do the splinters 'point' as the go into you? That is the direction of the frictional force. Nobody ever gets this wrong though it is a bit queasy to think about. This model does require that you have a correct freebody diagram.
Formal Physics Model of Friction:
A physics model is a description, often simplified, of a process. Models of all kinds only have value if they are useful and effective. Friction is a poorly understood feature of materials in contact with each other as mentioned at the top of the page. Our experience is that friction between two object depends primarly on two characteristics. The first is the actual materials that are in contact with each other. The other is how hard the two materials are being squeezed together. Think of holding onto a dollar bill when someone is trying to pull it out of your fingers.
Squeezy Force:
So how do we describe this force between two surfaces? imagine you are standing on a rope that someone trying to pull out from under your foot. Friction between the rope and your foot is what prevents this. As they pull harder you can keep the rope from slipping by putting more and more 'weight' on the rope. In the freebody diagram of your foot the force on the bottom of your foot in the freebody diagram is FN (the normal force). The bigger the normal force the more the rope is being squeezed by your foot. As a result we identify FN as the 'squeezy force' in our model of friction.
Coefficient of Friction (μ):
Many models, including friction, depend on empirical (experimental) measurements of material dependent characteristics. In the case of friction we are all aware that friction depends on the specific materials that are in contact with each other. It is common (though not universal) that these material properties are called coefficients of one sort or another. Another example is the coefficient of thermal conductivity which describes how easily heat moves through different materials.
The coefficient of friction is basically a ratio describing the magnitude of the frictional force, Ff, relative to FN. When μ = 1 that means Ff = FN in magnitude. μ typically has values between 0 and 1 though higher values are possible. μ = 0 is a description of a frictionless surface.
Direction of Ff:
In this model of Ff the direction is always parallel to the plane of contact between the surfaces. 'Sideways' in a more colloquial sense.
Static and Kinetic Friction:
We have lots of experience with friction and one of the things we are very aware of is that it takes extra 'effort' (force) to get an object moving across a floor but once it gets moving we can back off. This is an expression of the reality that friction between moving surfaces is different (usually less) than possible friction between static (no relative motion) surfaces. We define two coefficients of friction, μk and μs, representing the kinetic (moving) case and the static case. In general μk ≤ μs. As we will see static friction is a bit trickier than kinetic friction.
The Model:
After all of that discussion here is the basic physics and engineering model for friction between 'rigid' surfaces. In the end the Ff is just another force in our freebody diagram that feeds into our tools for determining what might happen from Newton's Laws. Much of what we do over the next months will just involve exploring and adding new forces to our list of possibilities but the analytic tools will remain the same.
Kinetic: Ff = μk * FN
Static: Ff ≤ μs * FN
Figure out the direction from the splinters:)
FN and Ff as components of Fcontact:
Both FN and Ff are forces that arise from the contact between two surfaces. It helps us visualize what is going on to approach them separately. ON the other had you could add them together to get a more generalized contact force that points in an arbitrary direction. In this sense FN and Ff are the perpendicular components of the contact force.
Revisit with Friction:
Now we are going to go back through all the same examples but now including friction.
Two objects but No Ramp:
In a more complex problem take each object individually and make a freebody diagram. Use Newton's 3rd Law to connect forces on the related freebody diagrams. For now we will consider this without friction.
Physics Ropes:
Ropes, or things like ropes, are a feature of many physical settings. When a rope is shown or described in a physics problem it is assumed to be an 'idealized rope' which is available from the 'Catalog of Ideal Physics Equipment' (finally somebody has built the catalog!). An ideal physics rope is weightless, unstretchable (inextensible), perfectly flexible, and infinitely strong. Cool stuff if you can get it. Real ropes are more like very strong springs with mass and that will wait for another day!
It is a property of all ropes, ideal or otherwise, that they can only pull and never push. This may be obvious but recognize that this imposes some expectations on your freebody diagrams.
Objects connected by a rope:

Similar but on a Ramp:
A Serious Problem to Set Up!:
One thing we need to sort out is how tension works in complex freebody diagrams like this and prudent choices of coordinate systems when ropes are involved. What it boils down to is let the axes follow the rope and keep + in the same direction as the movement of the rope if possible.
We will need to tidy up labels etc but start by making freebody diagrams of each object
[solution pdf here]
HW: Newton's 2D Friction
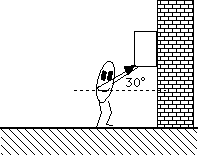
The person in the sketch is exerting the minimum force needed to keep the 100 kg block from falling down the wall. She is pushing at an angle of 30 degrees with respect to the horizontal. The coefficient of friction is 0.6. Determine the magnitudes of all the forces in the problem.
HW: Newton's 2D Friction
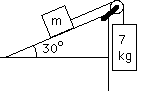
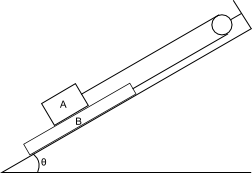
The static coefficient of friction between the block and the ramp is 0.4. What is the maximum mass m for which neither block moves? [is there a minimum mass of interest in this problem?]
HW: Newton's 2D Friction
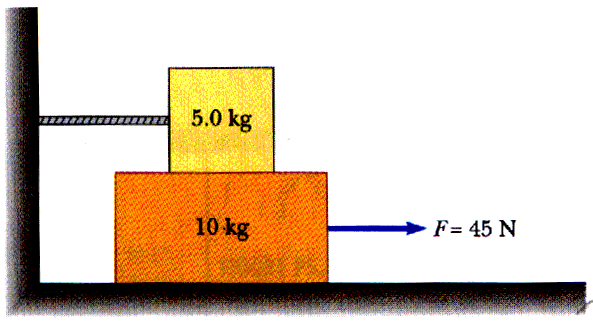
Two block are stacked as shown on a frictionless table. The static coefficient of friction between the boxes is 0.45. What is the maximum force that can be applied without moving either block? Take the time and trouble to make a careful freebody diagram for each mass with descriptive labels.
HW: Newton's 2D Friction
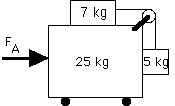
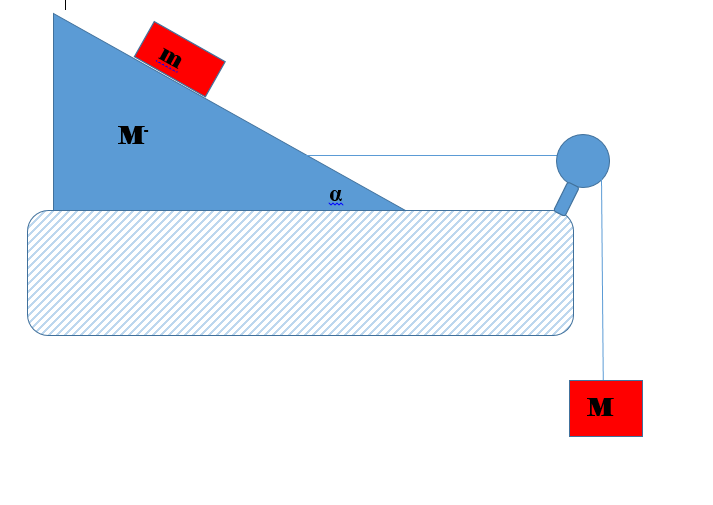
You apply a force FA to the 25 kg box on wheels in the arrangement of blocks shown. All surfaces are frictionless. For what applied force will all the blocks remain stationary with respect to each other? (Hint: What does this mean regarding acceleration?) This is a challenging problem and I don't necessarily expect you to get it but it is worth your time to try it and see if, or where, you get stuck.
Assignment: HW: Newton's 2D Friction
Turn in the various (4) homework problems in this breadcrumb. For these problems please be attentive to our problem solving format and guidelines for different styles of problems.
Assignment: Reading
While it is actually just a special case of 2D Newton's Laws so many objects move in ways which are circular or nearly circular that it worth taking some time to address this important special case. Read Circular Breadcrumbs.