Energy

Because of Newton's 3rd Law we expect that every force that adds energy is partnered by a force that is in the opposite direction and is therefore removing energy. This leads to the conceptual idea that energy should be conserved. This is not an idea that we can 'prove' from first principles but it makes sense from the 3rd Law and has never been found to be violated on this planet. On the scale of the universe there are some questions but the scale is really different.

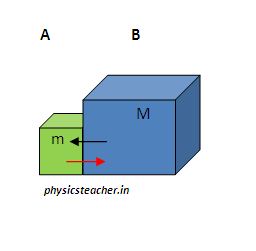
In the following setting the 'red' and 'black' forces represent a 3rd Law pair. Assuming both objects move to the right the 'red' force is adding energy to M while the 'black' force is removing energy from m. Since ALL forces have their 3rd Law pair it is a natural consequence to energy removed from one object is always added to some other object. In a nutshell this is why we

This the underlying rationale for conservation of energy.

 

Energy Bar Charts:

If we accept that energy is conserved then it is very helpful to have a tool to keep track of where that energy is. The tool we use is called an energy bar chart (though Khan calls it an LOL chart for reasons I don't understand). The energy bar chart is just a tool that expresses the work/energy theorem in a visual way.

These are references you can look at for another perspective

Kelly OShea's Blog: Energy Bar Charts

Khan Academy presentation:

Let's start by considering the work energy theorem as we have it now.

Because the change in kinetic energy can be rewritten as...

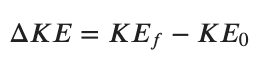
..we can then rearrange to get.....

In words what this equation says is "The initial kinetic energy of an object plus any energy added or removed equals the final kinetic energy of that object."

We can represent this with a bar chart like the following

...which looks like this with some values filled in.

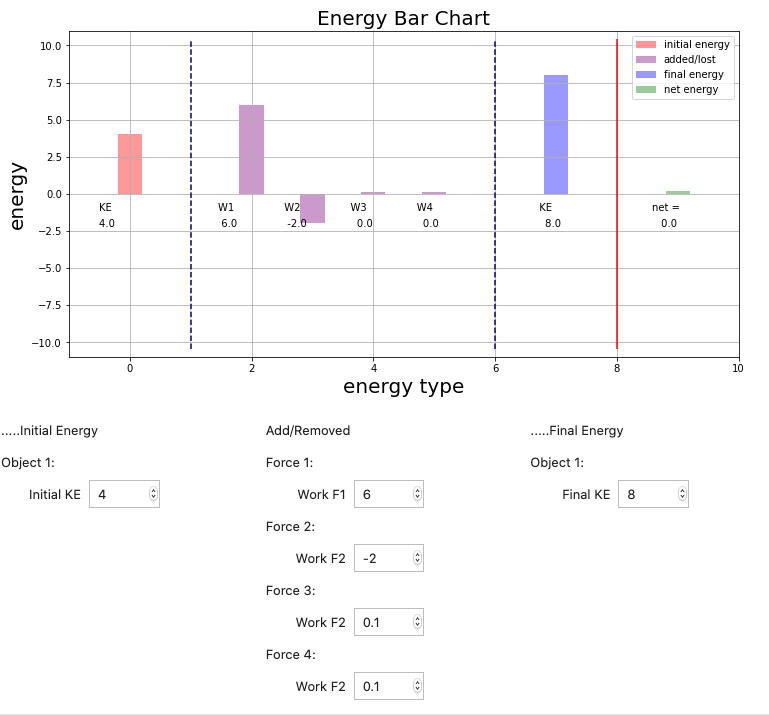
In this representation of the energy in the system every force on our freebody diagram (FBD) is represented by a bar UNLESS we can explicitly argue that it neither adds nor removes energy (the normal force is often an example). The 'height' of each bar can be determined and then the equation that describes the system can be written from the bar chart. All of the previous HW problems could have been represented with this bar chart.

Potential Energy:

Potential energy is an accounting tool for keeping track of energy. We will explore gravitational potential energy and spring potential energy in this class though there are certainly forms of potential energy. Be careful -- not all forces which move energy can be re-expressed as potential energy.

The basic concept is that for some forces (gravity and springs being some of them) we can show that the work done by such a force only depends on the end points of the process and not on the details of how the process proceeds between the end points. This is perhaps surprising and is NOT true of all forces that do work. Forces that meet this criteria are called conservative forces. Friction is clearly NOT a conservative force -- why?

In the case of conservative forces we can always get any energy removed back by simply returning the object to it's original location because of path independence.Conceptually we imagine that when a conservative force has removed some energy that energy is stored in a reservoir, like a bank account, that I can get it back from. Like bank accounts there is a sign difference between the sense of 'money' (energy) in or out of the reservoir and the sense of 'money' (energy) in your pocket (the object). Intrinsic to the idea of potential energy is the concept that it represents energy stored somewhere. It's not always clear where the energy is stored but, like a bank account, we are able to withdraw energy from where it is stored under the right circumstances. Springs store energy in way which we are familiar with. Batteries store electrical energy. Other forms of stored energy are a little less clear.

This conceptual discussion can be summarized in the following statement:

ΔW_F (the energy moved by the force F) = - ΔPE_F (energy in the reservoir for that force)

Gravitational Potential Energy:

While we can use calculus tools to make a concrete mathematical argument for the path independence of the energy moved by gravity we can also make a clear geometric argument. This is illustrated in the following image.



Any path between A and B can be represented as a series of 'steps' that are either perpendicular or parallel to the force of gravity. The total energy moved by gravity as I move an object from A to B will be the sum of the energy moved in all the parts of the path. Notice that on the sections of the path where the force of gravity is perpendicular to the path no work is done. This is because cos(90^o) = 0 as we discussed previously. Only the parts of the path where we move closer or further from the center of the earth 'do work' or move energy. The energy moved must depend only on r₁ and r₂, the end points, and not the path from A to B.

Down on the surface of the earth these two parts of the path are just small horizontal and vertical displacements. It is hopefully apparent that the work done by the force of gravity only depends on how high it is when we start and how high it is when we finish. Only the vertical steps contribute to the work. This leads us to the expression:

ΔW_Fg = - mg(h_f - h₀)

...where h is the height relative to some reference height and up MUST be positive. Check the sign to see that this expression says that F_g removes energy from an object that is lifted from the floor to the counter (h_f > h₀). Conversely it says that energy is added to an object that is 'dropped' off a counter (h_f < h₀).

From our conceptual definition of potential energy above this means that...

ΔPE_g = mg(h_f - h₀)

...where I hope you notice the change of sign.

Returning to our general expression for the work/energy theorem we can perform the following mathematical magic...



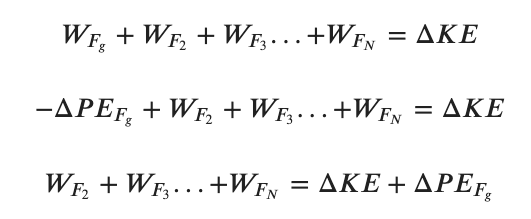
Where we have replaced the work done by gravity with it's equivalent change in potential energy. We can then rewrite this in the same way we did with kinetic energy ....



Note that the work done by F_g is no longer included within the square brackets since it has been accounted for using the potential energy. This then becomes a bar in our energy bar charts as shown below...

[insert bar chart here]

...which looks like this with values entered....



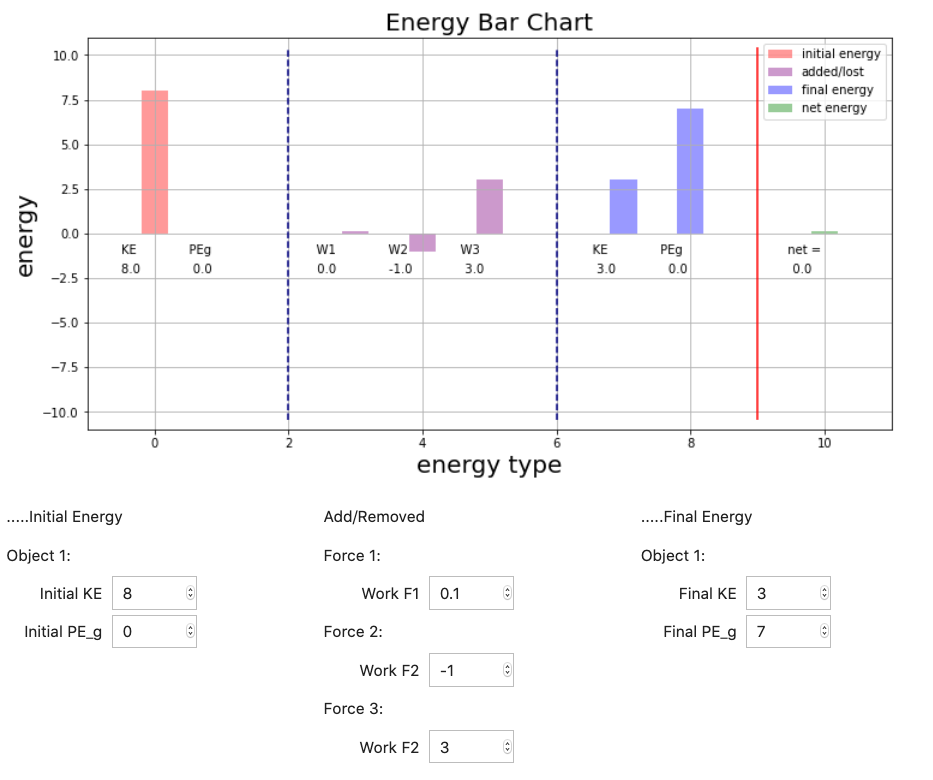
In this bar chart the height of each bar is given by one of the following expressions...



 

Sample Problems: Gravitational Potential Energy

Problem Solving:

Do a freebody diagram. Set up the energy bar chart for all forces that move energy (do work). Write the equation which represents conservation of energy and solve.

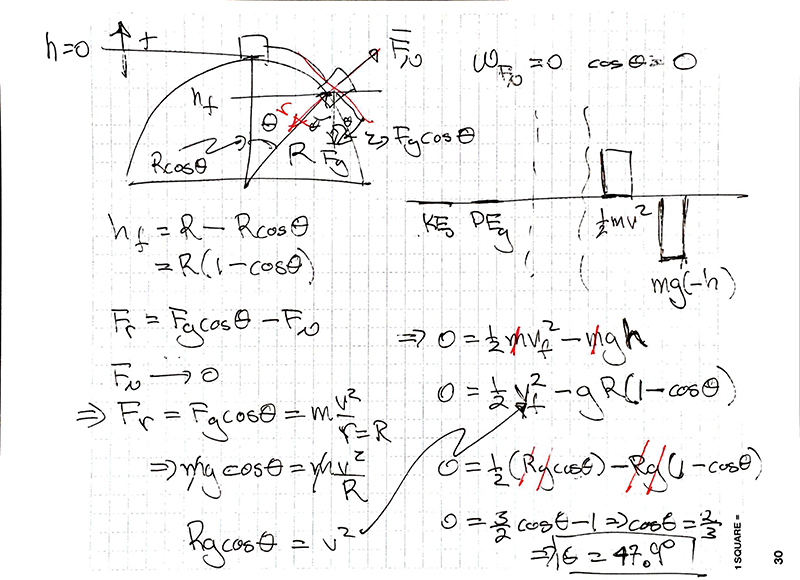
Loop the Loop:

The usual question here is how fast is the cart going at A and B. Can you determine the speed of the cart at any point along the loop? Could we do this with Newton's Laws?





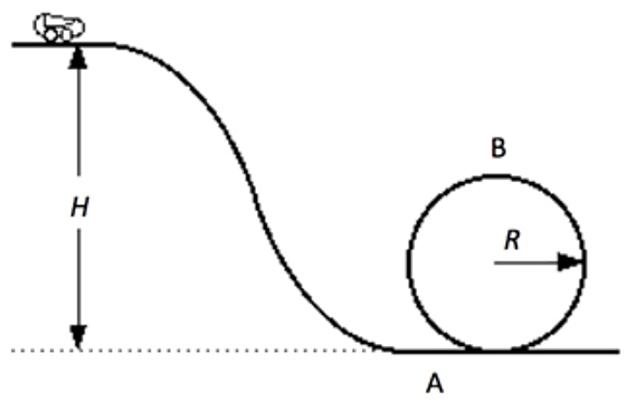
Students have pointed out that there was once a version of this setting at a waterpark in N.J.. As we will see in a future calculation it is quite difficult to acheive the speeds needed at the bottom to make it over the top never mind the 6g forces at the bottom. Use your physics and be smart if you meet one of these.



 

A similar problem...How do you set it up? What is the critical point where the object separates from the dome?





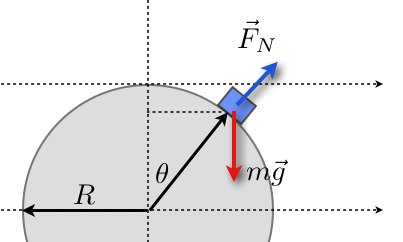
HW: PE Gravity

A skateboarder traveling 14 m/s enters a circular loop the loop which has a radius of 4 m. What is the speed of the skateboarder at each of the compass points of the loop - bottom, halfway up, top, and halfway down - assuming no losses due to friction.


HW: PE Gravity

Return to the 'Failure to Loop' sample problem in Circular Motion II. Given that v²_min = rg at the top of the loop determine the minimum speed that the skateboarder in the previous problem must have at the bottom of the loop to successfully negotiate the loop. What is the normal force on the skater as they enter the loop (answer in multiples of mg)?

Here is a thoughfully improved loop the loop being tested at a waterpark. Can you see the changes that were made and why they lead to a more survivable experience?

HW: PE Gravity

As you (80 kg) ski down a constant 15^o slope you find that you speed up from 10 m/s to 15 m/s over a distance of 100 m. Use energy methods to determine the amount of energy removed by friction between the slope and your skis. Assume the frictional force is constant and determine the magnitude of the frictional force.

 

Assignment: HW: PE Gravity

Turn in the various (3) homework problems in this breadcrumb. For these problems please be attentive to our problem solving format and guidelines for different styles of problems.

Assignment: Reading

We will dig deeper into the use of potential energy in the context of a serious astronomical event. Read Potential Energy II Breadcrumbs.