Energy (usually referred to as Work/Energy)

Energy is a concept that we use very commonly and casually in our daily lives but we are not actually very clear about what it is. Never the less it is a tremendously valuable and useful concept that allows us an alternative way of understanding many settings and problems of interest. Along with Newton's Laws this is the other important idea/concept to try to master from this term.

What is energy?

Good question! At this point in the development of our scientific perspective on the world energy is the root of everything that happens. This perspective has taken centuries to develop so it is important to note that many of us may be significantly unclear about energy.

One of important part of this question of 'what is energy?' is to clarify whether energy is a 'thing' like a rock or water or is it a characteristic that something might have? To explore this we can start, as I often do in class, by asking you to consider what you would put in a jar if I asked you to put some 'energy' in the jar but only energy and nothing else.

Activity: If you are working through this material independently take a few moments and think about what you would 'put in the jar'. In each case ask yourself whether the thing in the jar 'has' energy or 'is' energy? To test this can you imagine the same material in the jar with a different amount of energy without it being observably different. If so then the material 'has' energy.

People have a range of suggestions for what to put in the jar. Consider the following question about what you might put in the jar. "Is what I put in the jar energy or does it have energy within it?". For example, if you put gasoline in the jar, can I remove all the energy (burn it) and still have all the physical material that made up the gasoline? That would suggest that gasoline HAS energy rather than IS energy. Light is often suggested as something to put in the jar. If I slow the light down, which I can do, is the energy the same?

The conclusion I hope reach after exploring this for a time is that energy is a property that many things can have more or less of but it is distinct from the thing which contains or holds the energy. Sometimes there is no externally observable way to tell whether something has more or less energy.

Kinetic Energy: Qualitative

One consistent observable feature of objects that we associate with energy is movement. Objects which are moving faster are consistently idenitified with having more energy than the same object moving slower. This is a specific type of energy that we will label Kinetic Energy (KE for now).

Forces and KE: Relationship

To make an object move faster requires forces at least according to Newton's Laws. Part of the structure of all the sciences is the expectation that the various perspectives within the discipline are related to each other with some consistency. We have explored the ideas embedded in Newton's Laws which seem to apply to our physical world and if this kinetic energy thing is going to be consistent it will require forces to make more or less of it.

Be aware that there are other forms of energy where it is less apparent that forces are or are not involved.

Formal derivation of Work/Energy Theorem:

We start where many many physics discussion start which is with Newton's 2nd Law

This is the work/energy theorem!

What this says is the energy added or removed by ALL of the forces (F_net) acting on an object will result in a change in kinetic energy of the object. This expression gets more nuanced in other settings but for the mechanical world of physical objects this is a good version.

Take Home:

If energy is added the kinetic energy of the object increases, if energy is removed the kinetic energy of the object decreases.

If the kinetic energy increases then something adds energy to the object, if the kinetic energy increases then something removes energy from the object.

Units:

Looking the right side of the expression we would say that KE (0.5 mv²) has units of kg(m²/s²). Looking at the left side (F dx) we have N-m = kg m²/s²-m = kg(m²/s²). This is how it has to turn out if the math is legit! This collection of units N-m = kg(m²/s²) is called a Joule and is abbreviated J. We will discuss in a minute the size of a Joule.

Joule (J) = N-m = kg(m²/s²)

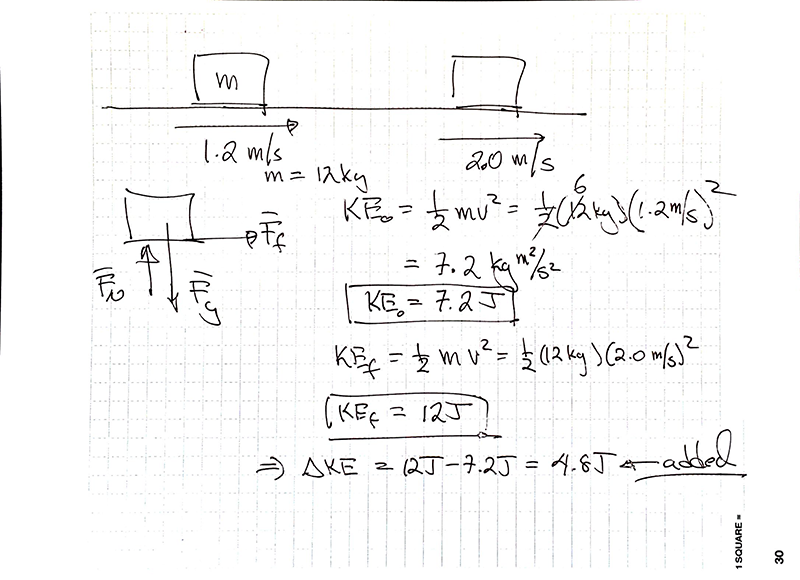
Practice Problem:

Imagine a 12 kg package moving down a conveyor belt at 1.2 m/s. How much kinetic energy does it have? A little later it is moving 2.0 m/s. How much kinetic energy does it have now? Was energy added to the package or removed from it? How much was added or removed?

The Left Hand Side:

Energy moved by F (F = constant in magnitude AND direction):

This discussion applies to an INDIVIDUAL FORCE. F_net is the combination of several or many individual forces. When the force is constant then determining how much 'work is done' (how much energy is moved) is relatively straightforward and is summarized in this image below. Notice that what we are asking, from the previous discussion of the work/energy theorem, is how does a force add energy to an object that results in an increase in kinetic energy (due to speed). Look at the image below notice that only the horizontal component of the force can add to the speed of the object. There is no acceleration in the 'y' direction.

This is the form of this expression I would like you to use because it indicates that the angle θ is BETWEEN the direction of the force F and the direction of the movement (Δ x). This is a helpful mnemonic.

Consider the same case but with the force acting (at the same angle) to slow the object down. In this case the angle BETWEEN the vectors is (180^o - θ) and cos(180^o - θ) = - cos(θ). The implication is that the same amount of energy is moved but it is removed (indicated by the (-) sign) rather than added.

W_F > 0 (positive) describes energy being added

W_F< 0 (negative) removes energy being removed

Dot Product:

The dot product is a particular way of multiplying vectors. It expresses a similar relationship between two vectors as that described above with F and Δ x. Here is how it is usually portrayed.

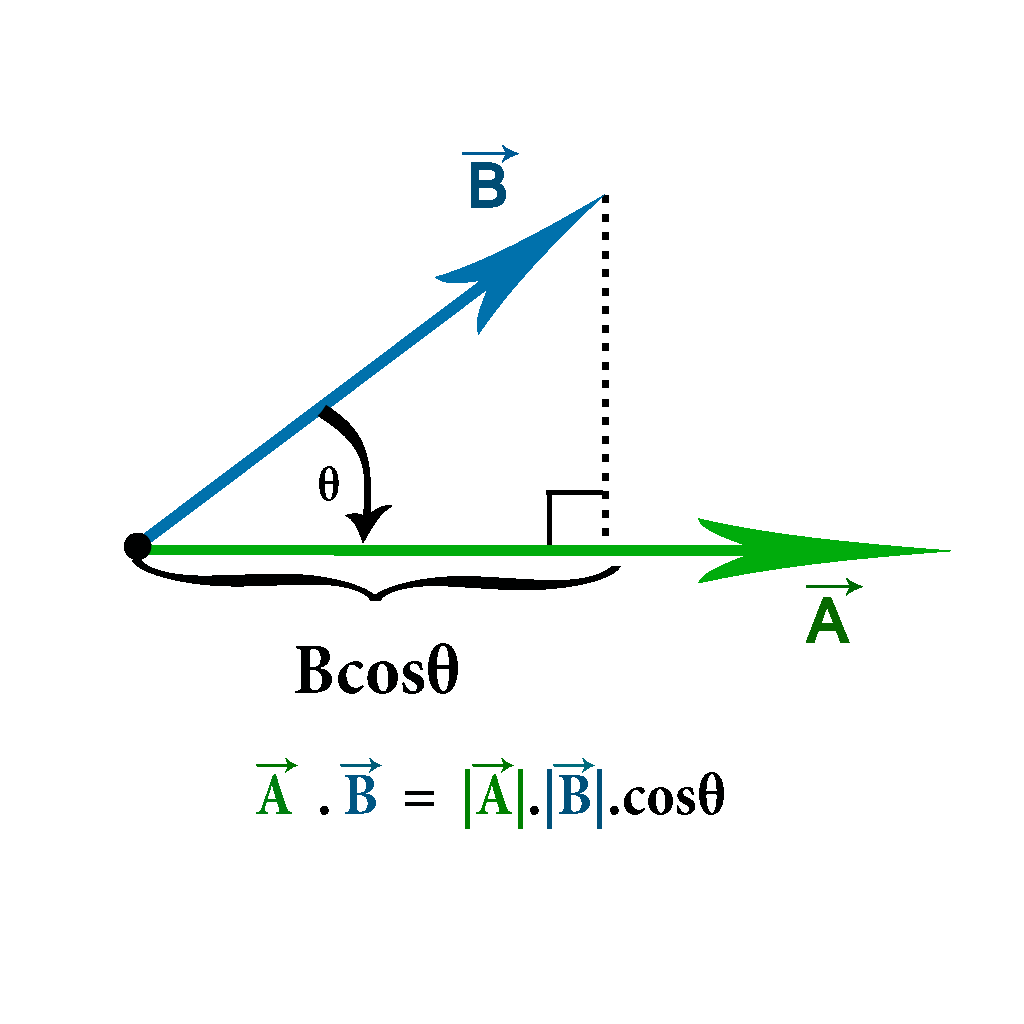
Notice that the result is NOT a vector. Notice also that it doesn't matter which order we do the dot product. Mathematically the dot product is commutative. Mathematically we say....

The dot product is often described as picking out only the part of B that is in the direction of A and multiplying them. Note that again I prefer to keep the cos(θ) term BETWEEN the vectors to remind me that it is the angle between the directions they are pointing.

If the force is not constant in either magnitude or direction then we do the calculus thing of taking small Δx's such that Δx = dx and we end up here.....

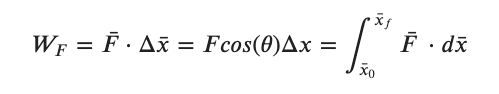
NOTES:

Students often refer to this as the 'work force' which is misleading and sounds like a government report. This language, "Work done by F" or the "Energy moved by F", is more appropriate and helpful. Most of what we will do this year deals with constant forces so a need for the integral version is rare.

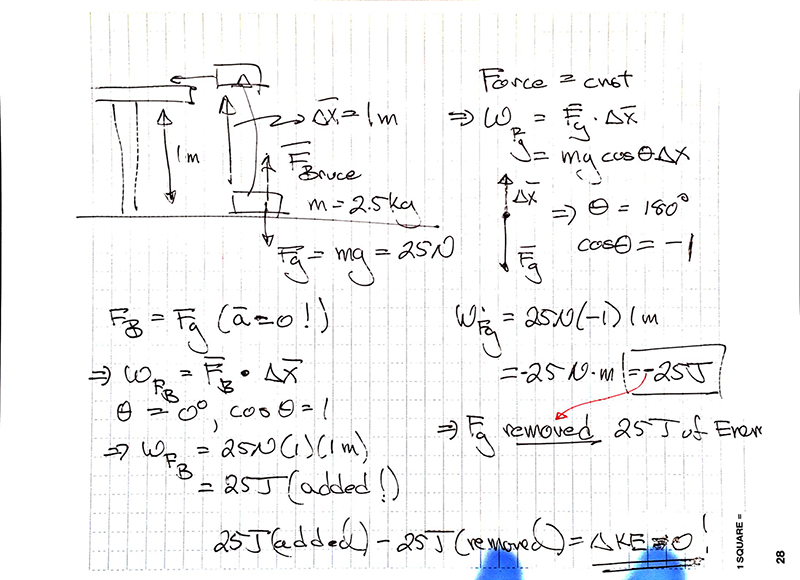
Practice Problem:

Imagine you pick a physics textbook (mass = 2.5 kg) up off the floor and set it on the counter which is 1 m above the floor. The text moves at a constant speed vertically except for a moment at the beginning and the end of the process. How much energy was moved (work done) by the force of gravity during this process? Was this energy added or removed from the text? How much energy was moved (work done) by the force you applied to lift the book from the floor to the counter? (Do you know the magnitude of that force?). Was this energy added or removed?

 

Energy is a Scalar:

Energy is a scalar (number) and not a vector. We speak about the energy an object has but that energy has no sense of direction. This is an important distinction between forces and energy. There is a sign associated with energy that describes whether the energy is being added or removed from the object in question.

Units: What is 1 Joule?

Here is how xkcd thinks about a joule and what it can do...xkcd:)

If you consider the freebody diagram of a cup of coffee being lifted gently to your lips the gravitational force is about 4 N (0.4 kg) and you're moving the cup about 0.25 m which means each time you 'pump the mug' that's 4 N x 0.25 m = 1 N-m = 1 Joule (roughly). Your take away should be that a Joule is a small amount of energy. 1 kWh of electrical energy that you buy from Pacific Power for $0.10 is 3.6 MJ!

HW: Basic Work

In 1972 a large meteorite passed across the western US and was seen (in daylight) by many observers. It was estimated that the mass of the object was 4^.10⁶ kg and its speed was 15 km/s (typical of most meteorites). What was the kinetic energy of this object? Express this energy in Megatons of TNT (1 Mton TNT= 4.2^.10¹⁵ J). The Hiroshima bomb had a yield of 13 kilotons of TNT.

[0.11Mton]

HW: Basic Work

A box is placed on the bed of a flatbed truck. Consider the work done on this box by the frictional force due to the bed of the truck. In each of the following cases determine if the work done is positive, negative, or zero. This is entirely about the 'dot' in the dot product!

i) If the box is dragged along the bed of the stationary truck?

ii) If the box remains at rest on the bed of the truck as the truck moves down a straight road at constant speed.

iii) If the box remains at rest on the bed of the truck as the truck moves down a straight road at increasing speed.

iv) If the box slips backward relative to the truck as the truck moves down a straight road at increasing speed.

[-,0,+,+]

HW: Basic Work

In 1955 an 80 kg paratrooper discovered during an exercise that he had a nonfunctional parachute. He landed in a snowbank and amazingly survived. His speed as he hit the snowbank was estimated at 50 m/s and subsequent measurements determined that he blasted approximately 1.0 m into the snowbank. Use energy methods and Newton's Laws to estimate the average force he felt as he was brought to rest. Of course you remember that average forces are always constant?

[1.0^.10⁵ N]

HW: Basic Work

A 5 kg block, initially moving 4 m/s, slides 3.0 m down a ramp that is inclined 15 degrees above horizontal. The coefficient of friction is 0.2. Calculate the energy moved by each force (all are constant). Add them all up and they will indicate the change in the kinetic energy.

i) How much work is done on the block by the gravitational force as the block slides down the ramp?

ii) How much work is done by the normal force as the block slides down the ramp?

iii) How much work is done by the frictional force as the block slides down the ramp?

iv) What is the total work done on the box by all forces acting on it?

v) How fast is the block moving after 3.0 m?

[roughly +50 J, 0 J, -29 J, +11 J, 4.5 m/s]

Assignment: HW: Basic Work

Turn in the various (4) homework problems in this breadcrumb. For these problems please be attentive to our problem solving format and guidelines for different styles of problems.

Assignment: Reading

Now that we have some basic tools to determine the energy added or removed from an object we will move on to broader applications of the work/energy theorem. Read Work/Energy II Breadcrumbs.