Work/Energy Theorem: Digging Deeper
The Work/Energy Theorem expresses the relationship between the energy moved by the net force in the problem and the change in the kinetic energy of the object. Remembering that Fnet is not an actual force but the single mathematical force that would produce the same effect as the combination of individual forces it represents.

This last version of the Work/Energy Theorem tells us we can determine the energy moved by each force in the problem. The sum of all those energies, being careful about signs, will determine the change in KE of the object.
Activity: Revisit the last HW problem on the previous breadcrumb with the block sliding down the ramp. Notice that you determined the energy moved (WF) for each force on the freebody diagram. After adding them up it allowed you to determine the change in kinetic energy of the block.
Work/Energy and FBD:
Because the Work/Energy Theorem is based off of Newton's Laws and reflects the energy moved by every force in the problem Freebody Diagrams (FBD) are still needed. Partly this is so we understand the relationship between the geometry of the forces and the geometry of the movement. In at least some cases you will need to know the angle between the force(s) and the movement due to the dot product. In addition the FBD gives us a tool to make sure we have considered all the possible sources of energy in the problem. Every force on our FBD has a corresponding term WFi in the work/energy expression above and must be accounted for.
Forces Perpendicular to Δx:
On our freebody diagram we may have individual forces that are perpendicular to the direction the object is moving. This include the normal force on a block sliding down a ramp. The tension in a string for an mass moving in a circle. The force of gravity when an object is moving across a flat floor. This is because cos(90o) = 0 in the expression for the energy moved by such a force.
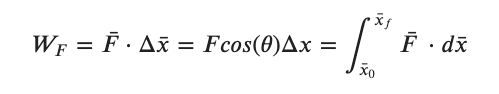
Power:
It's like your paycheck.....
We are all pretty clear about the difference between our hourly wage ( a rate in $/hr) and the money we get in our paychecks. To figure out the size of our paycheck we have to multiply our hourly rate times the hours we worked. $$ = rate*time. That should seem very familiar from our discussions of speed (a rate) and distance. Yes there might be some special corrections due to overtime. People are rarely confused by this calculation.
Power and Energy:
Power and Energy have the same relationship as your paycheck and your hourly rate. Power is the rate at which we use or produce energy. In an average sense it is the work done (energy moved) divided by the total over which the process takes place. We can certainly express the power provided or used for each force in the problem although the overall power is often of more general interest.
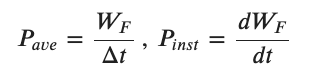
Sometimes we have enough information to determine the instantaneous power Pinst which is a derivative. Like energy power is a scalar and has no direction. The (+) and (-) signs indicate the direction of flow of the energy.
Power Units:
Given that powe is energy (J) divided by time (s) then we have J/s as the unit of power. 1 J/s is called a Watt (W). since a Joule is a pretty small amount of energy (coffee cup pump) a Watt is also a small unit of power. Your cell phone charger uses roughly 20 W when your phone is attached and about 1 W when it is plugged into the wall but not your phone. This is a tiny amount of 'vampire' power consumption.
Activity: This might be a good time to consider what the power output of a human body is. One way to think about this is to imagine how many light bulbs you think a human can keep lit if we put them on a bike connected to an electrical generator. While you might be tempted to worry about efficiencies it the system with modern DC generators the overall system is about 90% efficient at delivering electrical energy from a human being. Keep in mind that 1 horsepower (hp) is considered to be 745. What do you think a human can deliver short term or over extended times.
Sample Problem:
The Scott Firefighter Stairclimb is an event held in Seattle each year. As part of that competition firefighters in full turnout gear (+20 kg) race up 69 stories (240 m). The record in 2016 was 10 min 38 s. Lets assume that you make the climb in exactly 11 min. What is the power output of the firefighter? The energy involved is 'just' to lift your body up those stairs! Take your mass to be 85 kg before adding the turnout gear. The winner in the master's division (over 40) had a time of 15 min. This will give you a sense of how hard it might be to power light bulbs or other electrical equipment using the human body.
Assignment: HW: Work/Energy
An 80 kg bricklayer figures out a great way to get a free ride 10 m to the top of the building. He ties a rope to himself that goes up and over a (frictionless) pulley where it is tied to a partial pallet of bricks with a mass of 100 kg. The bricks are 10 m above the ground so he figures that when the bricks get to the ground he will arrive at the top of the building. What has he forgotten? How fast will he be going when he gets 10 m above the ground? This problem is inspired by the Ballad of the Bricklayer.
[7 m/s]
Assignment: HW: Work/Energy
This is a silly logic problem but is a good test of your ability to write down what you think the problem means and keep track of symbols. A man racing his sister has half the kinetic energy of his sister who has half his mass. If he speeds up by 1.0 m/s he will have the same kinetic energy as his sister. What are the initial speeds of the man and his sister?
[2.4 m/s, 4.8 m/s]
Assignment: HW: Work/Energy
You are designing a freight elevator which must carry a total load of 1200 kg (including the elevator) 54 m straight up in 3.0 minutes. You choose a 950 kg counterweight to assist the elevator. The counterweight is attached to the the elevator over a pulley and moves in the opposite direction to the elevator itself. How much work must the elevator motor do to raise the mass 54 m? What power rating should the motor have to accomplish this task in 3.0 min? How many hp (horsepower) is this? (1 hp =746 watts)
[1.0 hp]
Assignment: HW: Work/Energy
(Calculus) In a spud gun the potatoe is pushed up the barrel by expanding hot gasses. The muzzle velocity of a typical 400 g spud is 30 m/s. The force on the spud is given by F(x)= K/(x+.08) where x is the distance along the barrel in meters. If the length of the barrel is 80 cm what is the constant K and what is the peak force on the spud? Because the force is not constant you will need to integrate but what and what are the limits?
[75 N-m, 940 N]
Assignment: HW: Work/Energy
Turn in the various (4) homework problems in this breadcrumb. For these problems please be attentive to our problem solving format and guidelines for different styles of problems.
Assignment: Reading
There are some forces that have helpful characteristics that allow us to keep track of energy in the work/energy Theorem more easily. That's where we're going. Read Potential Energy Breadcrumbs.
