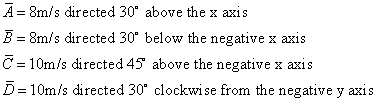Updated 1/18/19
For these vector problems use please sketch every vector at least roughly to scale on an x/y plot. Sketch the x and y components if relevant or sketch the addition and substraction of the vectors showing the resultant vector clearly. In each problem I expect to see an estimated solution before you use trig to determine the results more accurately. I'm trying to help you develop an awareness and intuition about the magnitudes (lengths) and directions (and the angles) associated with vectors.
1) What are the x and y components of each of the following vectors? I recommend doing this graphically first to clarify your estimates and then compare the results to those you calculate. Use signs to indicate the direction of the component relative to YOUR labeled coordinate system.
[A: 4 m/s, 6.9 m/s, D: -5 m/s, -8.6 m/s]
2) Given vectors A and B below determine the magnitude and direction of C=A+B, D=A-B, and E = A/2-3B? Do this first using graphical tools and without being too detail oriented. Compare this first result to that which you get by using component methods.
A = Ax + Ay where Ax = 4 and Ay = 6
B= Bx + By where Bx = -10 and By = +2
[C: 10, 53 degrees, D: 14.6, 16 degrees, E: ]
[d]
3) Suzie leaves her car and heads off due South for 2 km for a weekend hike. After 40 min she spies a cool rock formation off to the Northeast. She heads directly Northeast for 3 km and has lunch at the rock. After lunch Suzie strolls North for 1 km. On coordinate axes make a reasonable scale drawing of these vectors and determine the direction and distance she needs to travel to get back to her car.
[2.44 km, 28 degrees S of W]
4) Using 5 vectors defined relative to the cardinal directions describe how you could move from the NE door of the Science building to the hall outside Bruce's office (SCI 278). Each vector you define will have a length in steps and a direction. It doesn't have to be perfect but should clearly reflect the features of the geometry of the building.
[S,W,E of S,S,E]
5) Kayakers and canoeists know that by choosing their direction carefully they can move laterally back and forth across a river without moving upstream or downstream. Assume that the 25 m wide river is flowing at 2.0 m/s and the kayaker can maintain a speed of 3 m/s relative to the water. Be aware that the velocity of the kayak relative to the riverbank is the vector sum of the velocity of the water and that of the canoe or kayak (same is true of planes as well) What direction should you paddle to move directly across with river and how long will it take? How long does it take to cross the river if you paddle directly towards the far shore? How fast will you be going in this second case and where will you reach the far bank?
[about 40 degrees upstream and 11.2 s, 8.3 s, 3.6 m/s and 16.6 m downstream]