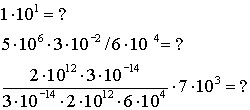These are all math skills that you are expected to have totally mastered with limited error rates. While that is a bit optimistic I will operate in class as if you can do these operations in your head as fast as you can do the x2 tables. Don't worry - you'll get lots of practice.

1) Write the simplest possible form of the following expressions. This is a chance for you to explore how simple you think you can make these expressions.

108/30=? 4a2b3/(b212)=? [3(7-2)-10]/(3+2)=?

[18/5] [a2b/3] [1]

2) Express the mass you would like to be in grams. (remember to use scientific notation) Mass and weight are not the same but are commonly confused in daily life -- go ahead and confuse them for now! [Bruce is about 1 ^.10⁵ grams]

3) Express the height you would like to be in kilometers. (remember to use scientific notation) [Bruce is about 2^.10^-3 km]

4) Compute the following without your calculator and then be sure you can get the same answer using your calculator.

[10] [2.5] [7/60=.12]

5) Express 9.8^.10^-10 m in nm (nanometers) and pm (picometers). [.98 nm, 980 pm]

Express π^.10^-10 s in Ms (megaseconds). [π^.10^-16 Ms]

6) (x+3)2=64 ; x=? 7) (x-4)(x+4)=9 ; x=? 8) (x+3)3 = (- 48x2)/6x5; x=?

[5] [5] [-1,-2]

9) Solve the following system of equations:

7x+3y=23 2x+5y=19

[x = 2, y = 3]

 

These next problems explore your comfort with differential calculus that you may have just completed.

10) A particle's position as a function of time is described by the expression x = 2t³- 6t +1 where x is measured in meters and positive x is towards the west.

a) What is the particle's position, velocity (dx/dt), and acceleration (dv/dt) at t = 2s?

b) During what interval(s) of time is the particle headed East?

c) During what interval of time is the particle accelerating to the West?

[a: 5 m, 18 m/s, 24 m/s/s, c: always]

11) Two cars are on the highway. The motion of one car is described by the expression x = 25t +5 and the other by z = 3t²+ t.

a) Are these cars ever at the same location? If so when and where?

b) Are these cars ever traveling the same speed? If so when and where?

c) Do these cars ever have the same acceleration? If so when and where?

[b: 4 s, 105 m, c: never]

12) Suppose in a certain atmospheric situation a raindrop with an initial mass of 10 mg collects smaller droplets as it runs into them. After 10 s it has a mass of 70 mg and a diameter of 5 mm.

a) If the droplet continues to gain mass at the same rate what will its diameter be at the end of the next 10 s?

b) Is 5 mm a reasonable diameter for a 70 mg droplet of water? Explain your reasoning.

Solve part a without explicitly using the formula for the volume of a sphere. The goal here is to use proportional reasoning rather than direct calculation. How does the radius of a sphere depend on its mass or conversely how does the mass depend on the radius? It will help, for part b, to know that 1 cubic centimeter of water has a mass of 1 g.

[6.15 mm, roughly yes]

13) A sphere of radius 10 cm is heated up so that its radius grows by 0.1cm. What is the change in volume of the sphere? There are at least two ways to approach this problem and I would like you to try both of the following and compare the results.

First: Take a direct approach and use the formula for the volume of a sphere to determine the volume before and after. In this case you will need to use your calculator to get a useful answer.

Second: Take a calculus approach and determine the rate of change of the volume of the sphere with respect to the radius by determining dV/dr from the formula for the volume of a sphere. You can solve this expression for dV = (stuff) from which you can calculate the change in volume. You shouldn't need a calculator for this one. Compare your answers.

[126 cc, 125.6 cc - really close]

14) The value of math in science is to provide a different way to describe the attributes of a setting or problem with clarity and appropriate precision. We often forget this as we learn to perform the incantations and rituals of mathematical manipulations. You will find that one of the learning tools that I find to be effective is to reverse the "traditional" direction of the problem. I have no doubt that you could find the equations from a story problem and solve them correctly. Can you do it the other way? What follows are two equations which describe a story. Can you write me a story for which these are the equations you need to solve (this is NOT a rhetorical question - go do it:). There are an infinite number of solutions but pay attention to what reality the equations are describing.

2a+b=15

2b-3a=16