In these problems the center of gravity refers to that point on the object where the mass of the object can be thought of residing.

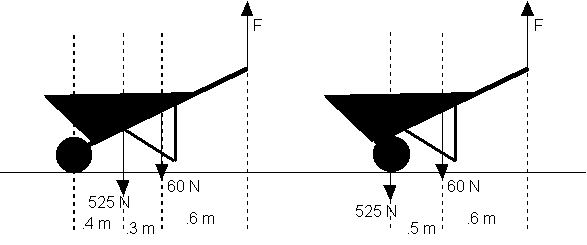
1) The structure of a wheelbarrow weighs 60 N and there is a 525 N load in the bucket. Two possible designs for the wheelbarrow are shown below. Calculate the vertical lifting force F required in each case.

2) When you are doing push ups (or in my case trying to) it is interesting to wonder how much of your weight you are actually lifting. Assume your mass is 72 kg, that your hands are 1.5 m from your toes, and that your center of gravity is 1.15 m from your feet. If you are in a horizontal position what force must your hands generate to keep you from crashing into the floor? What fraction of your weight is this?

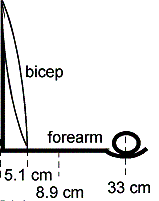
3) It seemed like it might be a good idea for each of you to go through this calculation again. A shot putter holds a 178 N ball in his hand. The forearm weighs 22 N and the center of gravity is located 8.9 cm from the elbow. All distances shown are relative to the elbow. What is the magnitude of the force from the biceps needed to hold the ball stationary?

4) When you (m=58 kg) put your hands on the wall at shoulder height (h= 1.5m) and lean into it at an angle of 20˚ with respect to the vertical you need to apply a force to the wall to keep your nose from being distorted. There are three forces acting on you and your center of gravity is 1.1 m from your feet. What force (in N) must you apply to the wall if you wish to remain stationary?

5) A car of mass 1750 kg has its center of mass located 0.6 m behind the front axle. The rear axle is 2.2 m behind the front axle. What is the magnitude of the normal force on each of the tires? (Consider what this means about the maximum frictional force that can be generated by the front and rear tires.)

6) One day, in a fit of boredom, you decide to determine the moment of inertia of a car tire. To do this you take the tire out on the flat driveway and give it a shove. As a result the tire cruises across the drive at an angular velocity of 8 π radians/s. You note that this acceleration took place over a time of 0.5 s and was the result of a torque determined to be 30 N-m. What is the moment of inertia of the tire?

7) (Calculus) A beam, 3.0 m long, extends horizontally from a building in the distant north where snow falls in abundance (sort of like Bend in some years!). Due to the prevailing wind snow has fallen on this beam in such a way that it is piled up deeper and deeper as you move away from the building. In fact the mass per unit length (λ in kg/m) of the snow resting on a point of the beam can be described mathematically as λ (x) = 1.5x +.5 where x is the distance from the building. What is the total torque exerted on the beam by the snow?