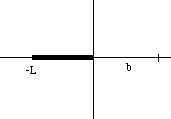Mood Brightener: ...more from Stay Homas. (Confination IV)

Integration problems in Physics: A model for addressing applications

What is contained in this document is my attempt to articulate how I think about the process of setting up and completing problems where I need to consider the collective effect of continuous distributions of something. This mysterious something could be mass or charge or current or force or....who knows. From my perspective these problems seem to share many common features and only the symbols change. I understand that for the student it seems more like a large list of highly individual problems that each have a particular preferred technique for solving them. It is much easier to be calm when they all seem the same than it is when they all seem different. Here then is my attempt to help you see how they are all the same.....

In time I will add some illustrations to this discussion to clarify what I mean but until I get that done you will need to work from these words and your notes.

• Lay out a clear (large) drawing of the setting so that you can clearly visualize the setting.

You need plenty of room to label variables and geometry as it becomes clear that you need to. In many cases the setting is 3 dimensional rather than just planar so try to be clear about this aspect of the problem.

• Choose a differential element that is a representative source of the effect.

At their root most physics principles describe the interactions of point like objects. To deal with continuous distributions we often need to "chop" the distribution up into small pieces which we can treat as point like objects. This is particularly common in problems from electrostatics and magnetism as well as engineering. In other settings where we have some distrubution of forces and we need to select a small piece of that distribution to use as a model for the behavior of the rest of the problem. What we are seeking to do conceptually is isolate a small piece of the source of the effect. We label this small piece of the source dq, dF, dm or d(whatever) where d (in the language of pidgin mathematics in physics) means "a small piece of".

• Write the physics expression for the portion of the effect produced by that differential element.

  This serves several purposes. One reason for doing this is to make you identify and articulate the physics tool that you use to describe the effect being sought. This might be a Coulomb force, or a torque, or an electric potential. You will also find that you need to label your drawing to identify all the geometric factors which are relevant to the effect you are seeking to describe. In my experience it is important not to worry about how the various labels are related but rather to be clear about what needs to be labeled because it is needed to describe the physics. Remember that as you are doing this you are describing "a small piece of" the effect and hence it needs to be labeled d(effect). For instance, dF is produced by dq, dV is produced by dq, d(torque) is produced by dm, etc etc.

• If you are dealing with a vector effect......consider this:

  Since you are about to add up (integrate) the vectors which represent the effects produced by each of the differential elements it may be necessary to consider the components of these vectors.

IF you can see that the vectors produced by each of the differential elements will be co-linear then this is essentially a one dimensional integral and you may proceed to the next step without concern (I can't think of a case where this is a problem though I worry that I'm overlooking something)

IF there is a lot of symmetry in the problem then you should look to see if that symmetry can be exploited to reduce the complexity of the problem. In many such cases a little careful inspection can provide convincing evidence that particular components of the vector will be cancelled by symmetrically located differential elements. With some experience you will come to know a small set of likely possibilities to try if there is symmetry in the problem. This is all about practice!!

IF there is no exploitable symmetry you are going to be doing a full blown vector integration which is a little outside the typical scope of this class. If I have some more time later I may flesh out this part a little but I want to talk to Charlie N. before I do so to avoid needless confusion.

• Setting up the integral - roughing it out.

Assuming that you have dealt with any vector issues in the previous step you now are ready to write down the integral of the expression you generated in the previous step. As I think about it I always envision that I am integrating the left hand side and just to be fair I also integrate the right hand side of the previously generated expression. If you are a traditionalist the left hand side will be the integral of dF or dV or d(torque) which integrates to F, V, or torque which is the collective effect you are seeking (admittedly there are some possible integration constants that are floating around here that we might need to be careful of). Consider the other side of your integral (that side which contains the sources of the effect) and extract outside the integral all terms which are constant for your problem. BE CAREFUL that you don't extract terms which actually vary as you consider different differential elements and visa versa.

• Setting up the integral - getting one variable and setting limits

At this point in the problem you will often find that you have a single differential element and several terms which vary as you move from one differential element to the next. The next goal is to find a clear mathematical label that identifies which differential element is being considered and express all the variable quantities in terms of that single label. This label is typically x or y for linear problems, it is often theta for angular problems, and could be anything else that is an effective means of distinguishing one differential element from another. From a physics perspective a variable is mostly a way of indicating a particular point which is what I mean by a label.

..or for surfaces

Once you have your integrand expressed in terms of a single variable (this may mean re-expressing your differential element in a manner analogous to your well understood u substitution process) it is time to set the limits of integration. One wouldn't normally expect this to be a problem but it is important to pay attention to what the minimum and maximum values of your particular variable are. The limits are often algebraic expressions themselves but don't let that worry you.

From conversations with the math department I think this is also a good place to check units. Be sure that the units of the terms in the integral combine to give you the units of your expected answer. Remember that the differential element (dx, dy, dq, dm, etc) has units too. Most of us check units after we go to the trouble of integrating but checking beforehand might catch an error in the set up and thats a good thing too.

• Doing the integration -- however you want but......

So now you have the integral set up and ready to go -- limits and all. Up until recently the next concern was the process of actually doing the integration which isn't always obvious. In the dark ages when I was in school (circa 1500) we had to use a range of techniques to complete the integration and we kept our treasured integral tables close at hand. In the modern era your calculators will do symbolic or numerical integration. For the purposes of physics and engineering you should generally do the integrals symbolically so that your result is in a useful form that allows you to change constants or other features at will. The ultimate goal in most of our classes is an understanding of our results not the actual number that comes out of the process. I have had a few experiences where the particular symbolic form of the integral reported by the calculator is much more obtuse and bizarre than it needed to be. I don't know the circumstances under which this happens but it is wise to be aware that there might easily be more than one way to symbolically represent the result of an integration.

Here's short clip exploring how I think of u substitution a little differently than the math folks....

• Check limiting cases for reasonable behavior.

  Don't forget to check the units of your answer at this point just to make sure things turned out well.

  As I mentioned in class I think this last step may be the most important skill I hope you develop. While we usually deal with settings in class that lead to results which are not revoltingly complicated when you are in the work world this is less commonly the case. You are likely to experience many cases where you work through a solution to a challenging setting and as you examine the result you have to wonder "Is this right?". An important part of verifying that you have a reasonable result is checking what your result tells you for special cases where you know what the answer should be. These are called limiting cases. You might know what should happen if one mass gets incredibly large and dominates the problem. You might know what should happen if you move the charges far apart so they both look like point charges to each other. You might know what should happen if you place the charge at some special place in the field. These kinds of questions ask you to look clearly and carefully at your result from the previous step and verify that it gives appropriate results under known circumstances. This is a very powerful and important skill to develop and will stand you in good stead down the road.

  If your result passes all these tests then you can sit back and relax with a well earned beverage of your choice.

   

  Here's a complete example for a uniform ring of charge. It works out a little too nicely but each step is there.

   

  Assignment Breadcrumb Reading: Bb Test

  Little Bits!

  Why do we cut up charge distributions into small "point-like" bits of charge? What is the physics reason that we need to do this?

  Before Next Class:

  Assignment HW: Bb Test

  Four Charges

  (practice notebook) Four charges of some magnitude are arranged in a square. One pair of opposite corners are positively charged and the other corners are negatively charged. What is the magnitude and direction of the force on one of the positive charges? Since you have had time to practice with the notebook the values on the test will be new to you.

  Assignment HW: Bb Assignment

  Pendular Proof

  Two tiny conducting balls of identical mass and charge q are hanging from insulating strings of length L. Show that the separation between the balls when they settle to equilibrium is (in the small angle approximation) given by

  

  Your solution will show all the steps leading to this result including the necessary approximation.

  If you need a hint here is an image of my freebody diagram to be sure you're started in the right direction. Notice that the tension in the string is nowhere in the expression above -- what does that mean?

  Assignment HW: Bb Assignment

  Line of Charge (Integration)

  A plastic rod 30 cm long (L) has a total charge of 5 mC (Q) uniformly distributed along its length. What is the force on a 10 mC charge located 10 cm (b) from the end of rod along the axis of the rod? Take the time to draw yourself a picture and work thoughtfully through the setting up process we talked about in class. Have fun -- we'll be doing lots of practicing on this stuff. Your answer will show the resulting integral complete with limits and the results of the definite integral.

  

  Looking Ahead:

  Look ahead to the next Breadcrumb: E Fields

  Assignment Breadcrumb Reading: Bb Test

  How to detect an E Field

  What is the basic tool by which we detect the presence of an E Field?