Mood Brightener: ...more from Stay Homas. (Confination XIII)
Kirchoff's Laws:
Like integration solving circuits using Kirchoff's Laws is a consistent and robust process that 'always' works for planar circuits (planar circuits are ones that can be drawn on a flat piece of paper with no crossing lines). If you are on a engineering or physics pathway you will encounter modified versions of this strategy in future circuit analysis courses but even those are actually just modifications of the basic use of Kirchoff's Laws.
Kirchoff's Laws are, at their root, just conservation statements that should seem consistent with the conceptual work we have been doing up to this point.
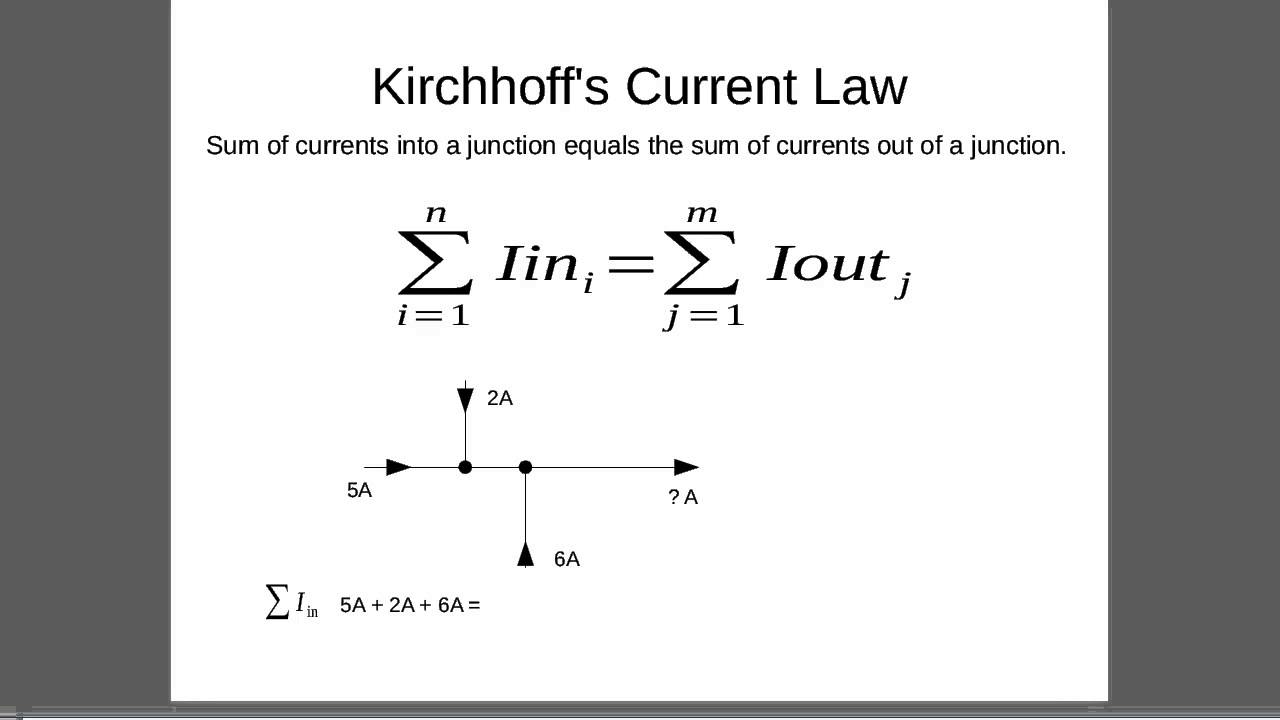
Kirchoff's Current Law/Rule (also called KCL, Kirchoff's Node Rule)
Conservation of Charge (Current):
We have developed a conceptual model which relies on the idea that the flow of charge through a circuit is consistent in a charges/second sense. In an unbroken wire the current must remain the same as the charges flow through any and all loads along that wire. In the event there is a junction the rate of charges flowing into the junction must match the collective rate of charges flowing out of the junction.
The sum of the currents entering a junction is 0! (given that currents flowing out are (-)!)
alternatively....
The sum of the currents entering a junction = the sum of currents leaving a junction.
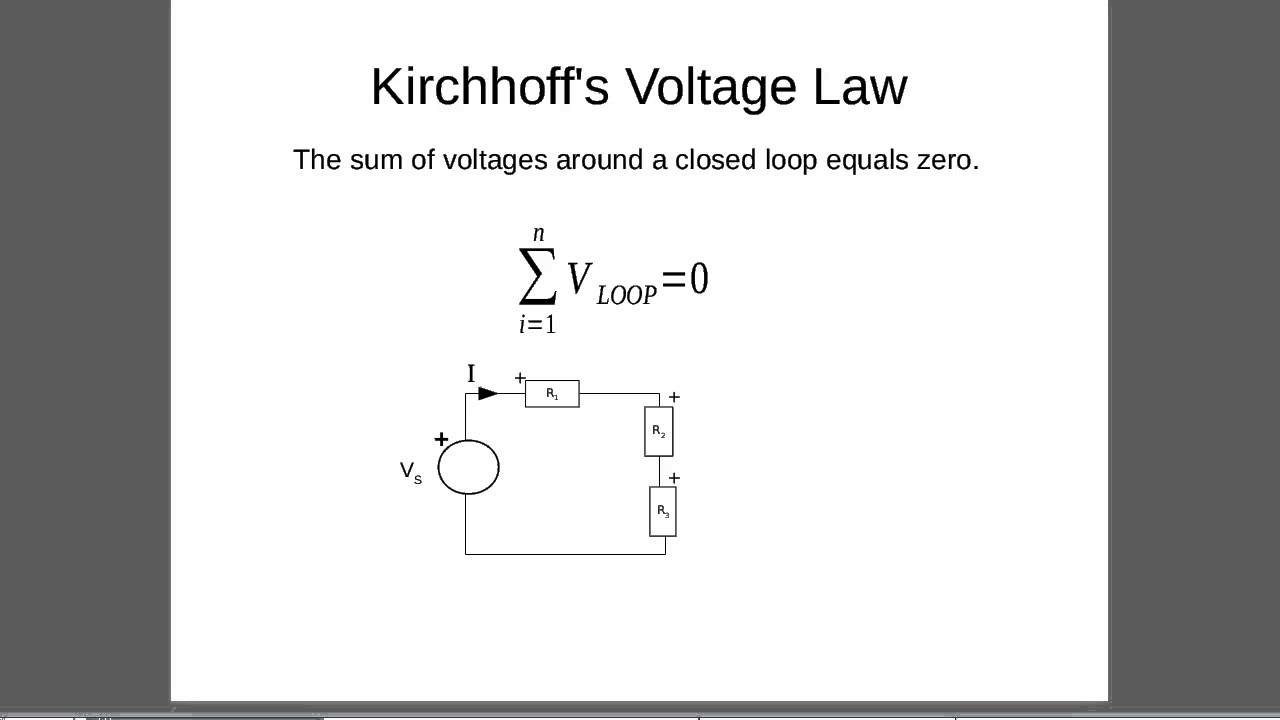
Kirchoff's Loop Law/Rule (also called KVL, Kirchoff's Voltage Rule)
Conservation of Energy (Voltage):
In our conceptual model we have also asserted that if the 'battery' is the factory that gives the energy to the charges which carry that energy to the loads then they must deliver all that energy before returning to the factory. If this didn't happen then the charges might slowly accumulate more and more energy as they complete multiple cycles through the circuit.
The sum of the voltage drops (energy delivered) around a loop = 0
To make sense of this mathematically one must assign meaning (+) and (-) signs. For us a good conceptual starting point is that (+) means energy added (in the battery) and (-) means energy delivered to the loads. Naturally this will be reversed in a future class just because.
Ohm's Law:
Finally we need to make more explicit our conceptual idea that the steeper the hill through a load the greater the current through that load. In the case where there is a linear relationship between the voltage drop (hill) and the current this is known as Ohm's Law. Not all loads are linear but circuit analysis always starts with linear loads (Ohmic Loads) because it describes many situations well and is a good starting place.
Mathematically it looks like this:
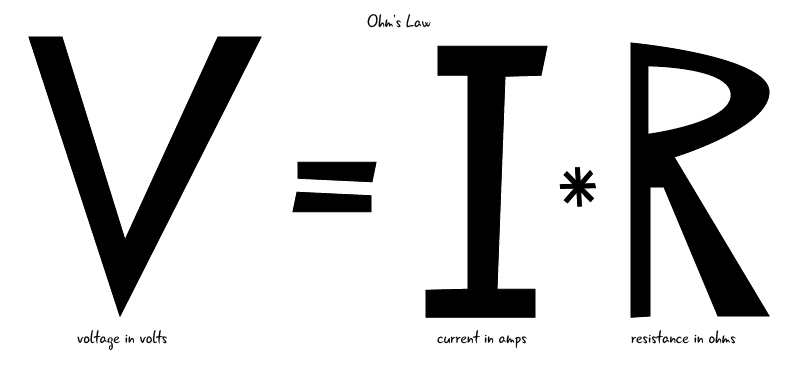
(thanks to the folks at Arduinotogo for the use of this graphic!)
For most applications we assume that R is a constant so that given a known voltage I can determine current. I am going to assume that you have no worries about any algebraic permutation of this expression. If you know any two of the quantities you can find the other!
Application:
We will use this process document as a guide to applying Kirchoff's Laws to a given circuit. We will use the process to address each of the following circuits in turn.
Series only with multiple resistors:
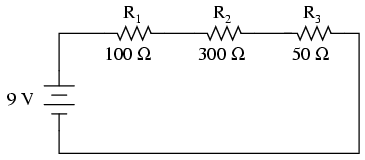
Resistors in Series:
You will note that the same current would flow from the battery if there were a single resistor of 450 Ohms. This leads us to the recognition that any unbroken chain of resistors in series can be replaced with a single resistor equal to the sum of the individual resistors without affecting the rest of the circuit. This single resistor is known as the equivalent resistance of the series of resistors.

It may seem obvious but it is important to notice that this expression means that the equivalent resistance is always larger than the largest resistor in series. An important conceptual idea.
Assignment Breadcrumb Reading: Bb Test
Ohm's Law:
Given a load with a resistance of 200 Ohms and a current of 20 mA what is the voltage drop aross this load if it is an Ohmic device?
Before Next Class:
Assignment HW: Bb Test
Node Rule:
Determine the current flowing in each resistor through application of the Kirchoff's Current Law/Rule.
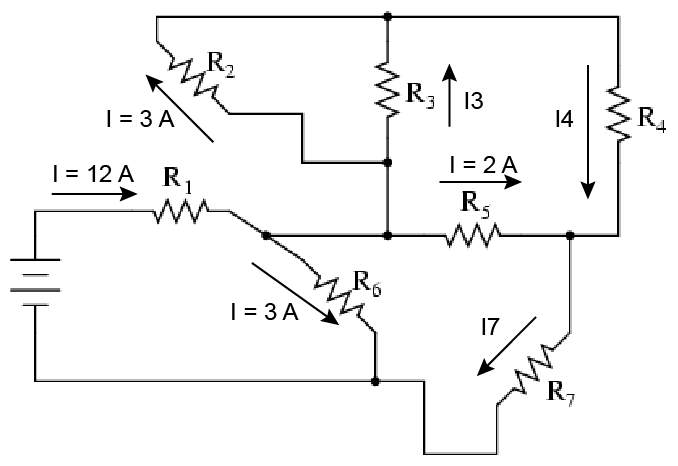
Assignment HW: Bb Test
Loop Rule:
Determine the two unknown voltage drops by thoughtful application of Kirchoff's Loop Law/Rule.
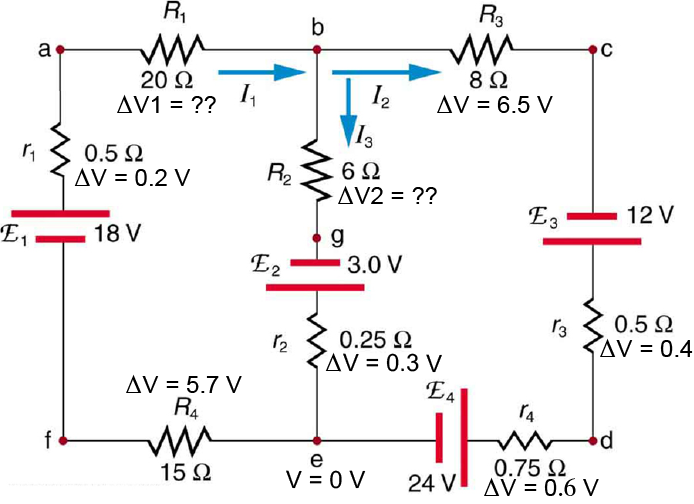
Looking Ahead:
Look ahead to the next Breadcrumb: Kirchoff's Laws II
Assignment Breadcrumb Reading: Bb Test
Resistors in Parallel:
Derive the algebraic result for the equivalent resistance of any two resistors in parallel. Note that it says the equivalent resistance is always less than the smallest of the two resistors.
