Mood Brightener: ...more from Stay Homas. (Confination IX)

Your Conceptual Goals for this section: E - ΔV Connection

Falstad Math/Physics Simulations:

How we really figure out fields and forces:

In spite of how we have constructed our ideas about Coulomb forces, E fields, and Electric Potential (ΔV) in practice we actually use these concepts in the opposite direction. Potentials are easier to measure directly and certainly easier to calculate because it is a scalar. From the potential we can differentiate to get to an expression for the E field and from there F_C=qE gives us the force we need to understand the dynamics. This week we will explore the tools and strategies that are typically used to describe an environment where there is an E field.

Equipotentials:

Starting with a uniform E field....

 

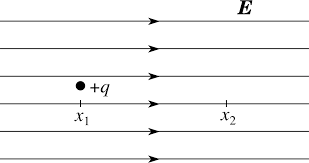
Start at some point (A) and move a test charge perpendicular to the E field to some other point (B). What is ΔV_AB? Can you find additional points B with the same characteristic? Do these points form a continuous line? Is V (ΔV relative to 'sea level') constant along this line? -- that's why we call it an equipotential.

Now, move your test charge some distance Δx with the E field. How will you determine ΔV_AB? Is B at a lower potential or a higher potential? Why do you say that? What does the equipotential line which contains this new B look like? If you move the same distance Δx again with the E field will ΔV_AB be the same or different? What if you move the test charge a distance Δx against the E field?

Now consider the E field around a single charge and do the same exercises....

Lets change the game a little bit. If I wanted you to draw equipotential lines that are all 5 V apart would the separation between equipotential lines be constant or changing? IF their spacing is changing where are they closer together and where are they farther apart? Can you articulate why this is?

Now lets try a more complex E field.... See what you come up with and imagine you are trying to keep the ΔV between the equipotentials constant (we'll explore in a moment why this is helpful). Be sure to note which equipotentials are at higher potential and which are at lower.

Questions, thoughts, other things you've seen like this?

Equipotential Maps:

Here's a gravitational potential map....

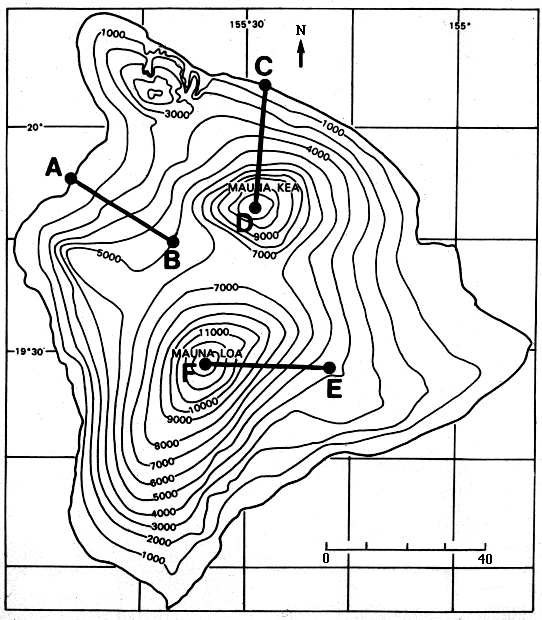
What is another name for this kind of map? What are the equipotentials? Why is it important that the equipotentials have the same potential difference between them? How many 'charges' are there? Which one is the biggest? Where is it steepest? How do you know?

How is this (electrical) equipotential map similar?

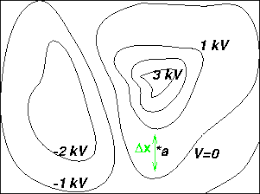
How many charges? What signs? Where is it steepest?

E Field is like "Slope" which is a spatial derivative:

On a topo map you can identify the direction of the slope of the hill because it's perpendicular to the topo line. Same is true for equipotentials and the E field. We also have the sense that the closer together the lines are (assuming equal potential difference betweeen the lines) the more intense the E field (greater the slope).

Stepping back to some previous stuff...

ΔV_AB = W_AB/q = [F Δx]/q = [qE] Δx/q = E Δx

which means

ΔV_AB = EΔx

and that can be rearranged to give

E = ΔV/Δx

which is a derivative in space rather than time.

Consider this map of potentials --- sketch the equipotentials and then determine the E fields at A,B, and C. The size of the grid is 4 cm between points

Now... this has been a very quick flash through the 'derivation' and I have made simplifying assumptions about the electric force being constant and in the same direction as Δx but I trust that you understand that exactly those assumptions will always be valid if I ask the question over a short enough distance (the calculus assumption).

Another Way of Thinking of the Slope on a Hill:

The next step along this path will be easier to understand (perhaps) is you take the following description and go out onto a hillside and experiment in different places. Imagine you are standing on a hill that slopes down and to the west. If are standing at that point an you lay a meter stick in the North - South direction is should be flat (no slope) and have some well defined slope if you put it on the ground in the East-West direction. Now move to some place where the slope is either towards the Southwest. Now when you lay your meter stick on the ground in the N-S direction it will have a slope and it will also have a slope in the E-W direction. Can you visulize the vector addition of those two slopes? If they are both the same then the hillside must 'point' exactly SW. If the N-S slope is bigger then the hill 'points' more south etc etc. This is not too hard to explain if I have you with me on a slope but it's a mess with words. I will try to make a video to help with this. [note: I looked for an existing one and nothing takes the perspective that aligns with this discussion in spite of many physics teachers using this as a model. Guess I'll have to make it myself]

dV/dx leads to E leads to ∇ (gradient operator):

[just as a weird aside I discovered that this symbol is called a(?) nabla (greek for harp) - never knew that]

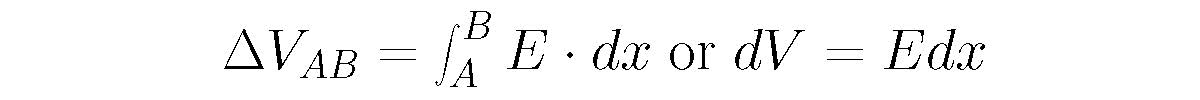
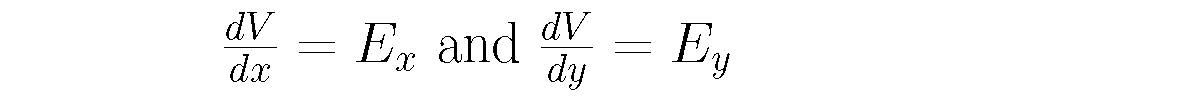
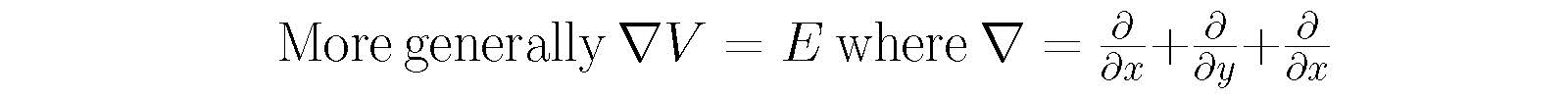
Now that makes perfect sense right?

Notice that this also means that E can be measured in V/m as well as N/C!! 1 V/m = 1 N/C -- slightly confusing.

Dielectric Strength:

So what if we now place a material which is NOT a conductor in an E field and slowly dial the E field up to greater and greater strength? Think about the forces on the + and - charges within a given atom. Does it seem plausible that eventually the E field forces seeking to pull the atom apart might exceed the atoms ability to hold itself together? What do you imagine happens at that point? This is the field at which an insulator becomes a conductor! When this happens in the air we get lightning or spark on the back of your siblings neck.

We call this dielectric failure and the strength of the E field that causes the material to become at least partially conducting is called the Dielectric Strength.

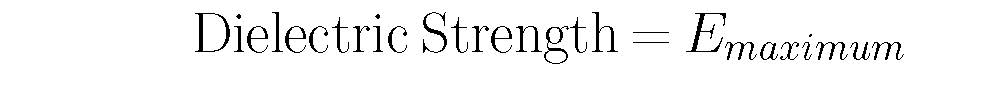
Here's a table of dielectric strengths for various materials. One to know for sure is E_max for air = 3 MV/m.

Assignment Breadcrumb Reading: Bb Test

Equipotentials:

Choose other data sets that share the same primary feature as equipotentials. There will be more than one correct answer. No, I didn't really mention this in the reading but you might consider looking up isotherms, isobars, and topological map lines.

Before Next Class:

Assignment HW: Bb Assignment

Sketching Equipotentials:

Given the E field shown below (taken from a lovely animated gif here) sketch the equipotentials. Be sure to show that you understand the core features of the relationship between the E field and the Equipotentials. Spacing between your equipotentials should attempt to correlate with the intensity fo the E field.

Assignment HW: Bb Assignment

Sketching E from Equipotentials:

Given the equipotential map shown below sketch the E field lines that are consistent with the map. What is the sign of each charge 'shown' on the map and their relative magnitude. Yes, these are isobars but treat them as if they were equipotentials.

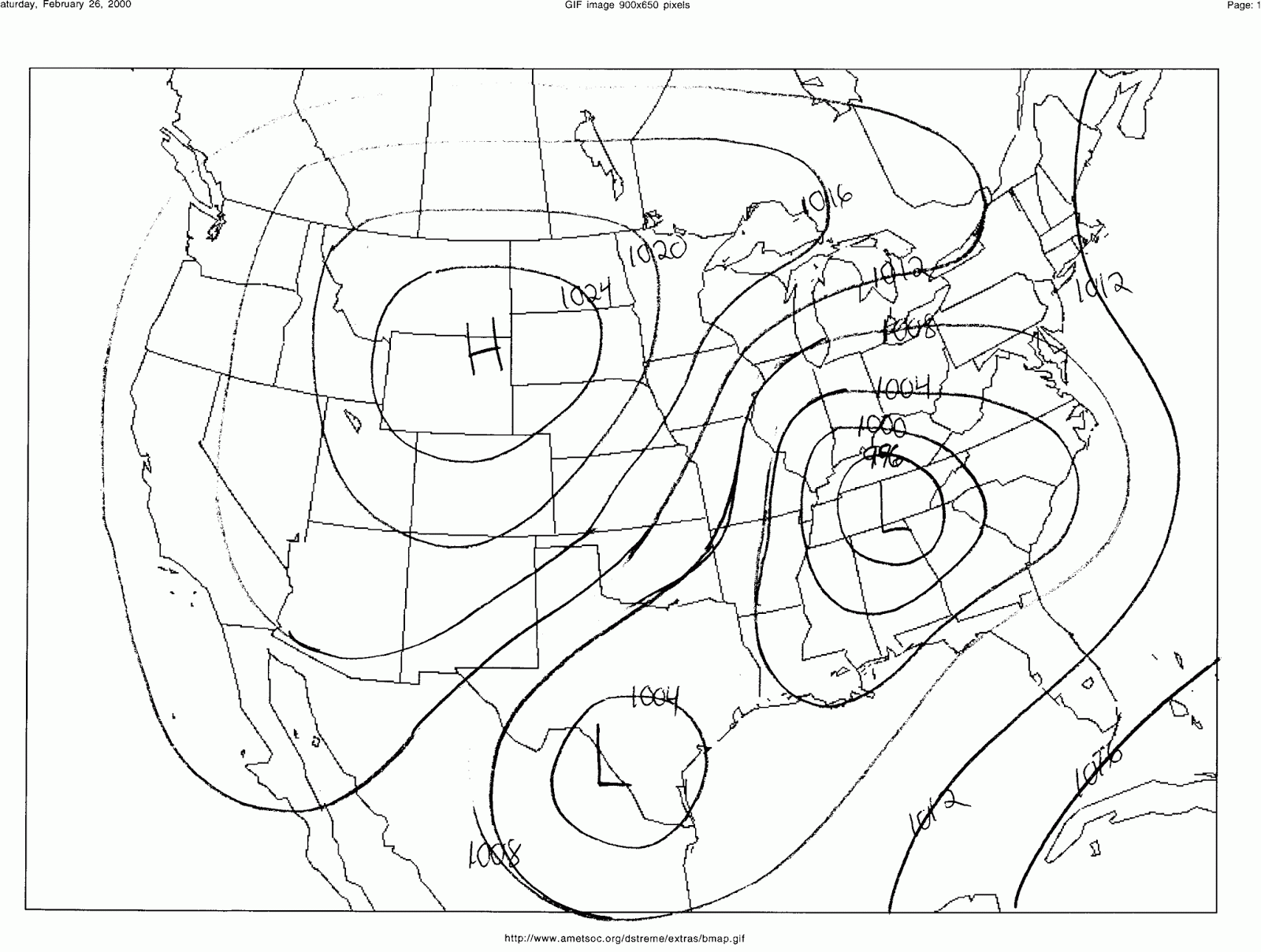
Assignment HW: Bb Test

Dielectric Strength:

I hope that everyone has shuffled across a rug and shocked a parent or a sibling some time in their life. To make this happen the E field between your finger and the 'victim' must be equal to the dielectric strength of air. Given that the dielectric strength of air is 3 MV/m what is the voltage difference between you and your 'victim' if the spark is 3 mm in length?

Looking Ahead:

Look ahead to the next Breadcrumb: DC Circuit Concepts (Circuits I)

Assignment Breadcrumb Reading: Bb Test

Conservation of Current:

When current flows through a circuit there are various ideas that we have about what happens when that current enters and exits from a light bulb. If 0.5 Amps of current enter a light bulb how much current exits the light bulb?