Faraday's Law (or 'How we make electricity!'):
Never mind that this section is all about Faraday's Law it is a great place to give a shout out to a unique figure in the history of physics and engineering. In a time when most scientists were folks of independent means who had external resources to support their investigations Faraday was a regular guy who became the model for an experimental scientist. His 'lab reports' are so comprehensive that we can use them today to fully replicate his equipment, because he had to build everything himself, and his processes. The Royal Institue of Science gives you access to many of his actual papers from their pages dedicated to Faraday. I find them endlessly fascinating.
Sidebar Conversation: Electric Motors (DC)
Depending on our timeline we may step aside for a few moments to discuss how what we have explored so far leads to a conceptual model for DC electic motors. This is a useful exploration since DC motors are physically equivalent to AC generators which are based on Faraday's Law.
Moving Conductors in B field:
Let's start with a thought experiment. We know from previous discussions that moving charges feel forces in magnetic fields. So what would happen if a bar of copper (or other conductor) were projected through a magnetic field? There are, after all, charges in the bar and if the bar is moving so are they. Consider the different ways that the bar might be moving relative to the magnetic field. Are there some configurations where there are no forces? Make some sketches and discuss with your classmates.
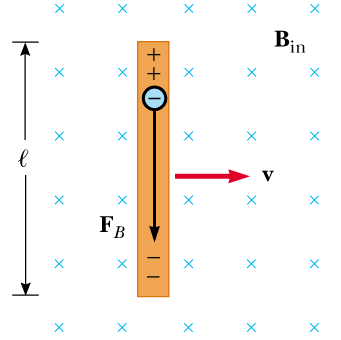
Activity: In your group start by considering the behavior of a single (-) charge as the copper rod flies through the B Field. As this first charge separates from it's parent atom what does the freebody diagram for the (-) charge look like (two forces)? When will those forces be balanced -- ever? Now consider a second (-) charge that begins to move? How does it behave differently? This is an important thinking exercise.
Regardless of exactly how the charges 'pile up' there will be a separation of (+) and (-) charge towards the ends of the bar in a dipole like arrangement. Well there be an E field in the bar? Why? Why does this not contradict previous discussions where E = 0 inside a conductor? If there is an E field in the bar does that mean there is a potential difference (ΔV) from one end of the bar to the other? Will the charges flow anywhere - why or why not?
Now consider that same bar moving through a B field but sliding along copper rails as shown below. From the perspective of the bar nothing has changed but connecting the ends with a conducting pathway creates new possibilities.
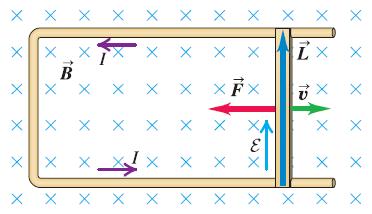
How does this effect depend on B, v, and L?
EMF (ΔV) = vBL
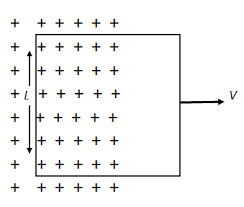
Now let's look for patterns....In each of the settings below consider whether there will be a current flowing around the loop. Use the same process that we used for the bar sliding down the rails previously.

..yes...
Activity: Will current flow around the loop in this version of the experiment?

...no...
...same one except spinning around a vertical axis instead of moving laterally.....

...no...
...yes, but in the opposite direction to the first case.
Now for some versions of this that I can't pilfer from the web.....
B field in the plane of the loop (compare to several of the above versions)
...no.....
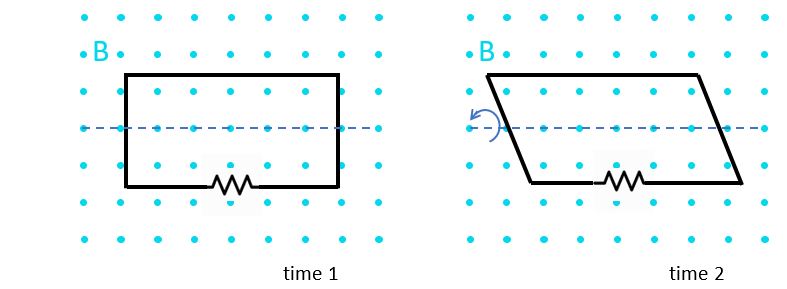
What if the conducting loop is make of a 'stretchy' material that will move in the sense shown.....
Activity: Will current flow around the loop in this version of the experiment?
....yes....
What if I have a fixed loop and turn up (increase) the B field? Start with the black and increase the field lines to get the green.
Notice that the field lines will appear to move inwards due to the increasing B field intensity...yes!
...and finally....
All of the ones that do generate a current moving around the loop might have some common characteristic. Any ideas what that pattern might be?
Flux in General:
We haven't talked about it yet but there is a concept called flux that was floating around at the same time physics was trying to understand all this. In it's most general sense flux is a description of how much of some quantity passes through a surface. There is an idea of flow since the most obvious example is the amount of water that flows through a gate or opening in some period of time (kg/m2/s). Imagine putting a window frame into a flowing river and asking how much water passes through the window. It depends on the size of the window, the speed of the water, the density of the water, and the orientation of the window relative to the flow. Makes sense yes? You can read about mass flux here if you want to look deeper into it. It's a commonly used fluid concept.
Magnetic Flux:
The same general idea applies to Electric and Magnetic Flux. The primary difference is that there is NO FLOW in the B or E fields in spite of the arrows and lines! Instead of 'moving through' think of the number of field lines that penetrate a given surface.
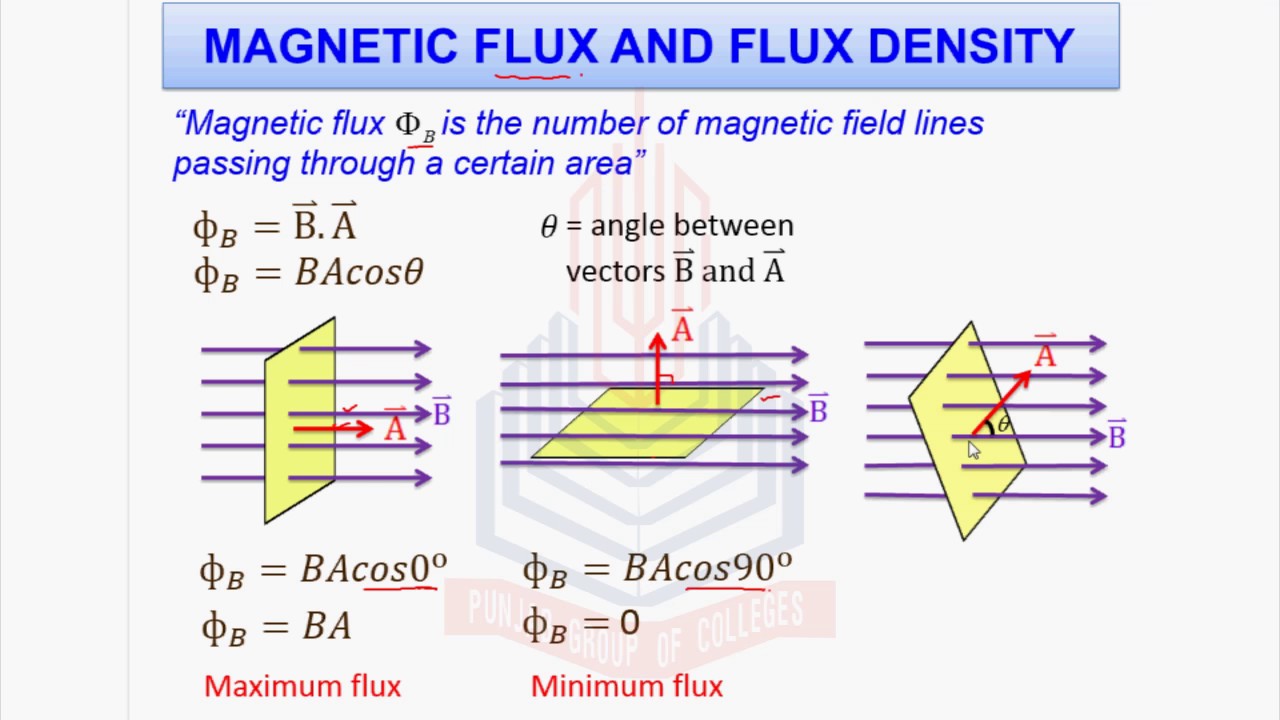
Notice in this image that it still talks about the B field 'passing through' which easily misleads into thinking about motion. NO MOTION HERE!!!! There is also a missing dot product in the expression at the top. What are the units of flux?
Flux (ΦB) = Webers (Wb) = T m2 - no telling why this has a name but it does. The E field equivalent does not!
HW Flux
As an initiation rite you are required to place your hand (area = 0.016 square meters) into a uniform 0.35 T magnetic field. What is the flux (ΦB)through your hand (ouch!) when the normal to your hand is parallel to the B field? When the normal is perpendicular?
HW Flux
A wire is bent in the shape of a 45-45-90 isosceles triangle. The B field is 0.35 T and the hypotenuse of the triangle is 14.14 cm. What is the minimum and maximum magnetic flux (ΦB) through this triangle?
HW Flux
A rectangular loop is spinning in a uniform magnetic field. The loop has an area of 0.15 m2 and the axis of rotation is perpendicular to the B field. If the loop is spinning at an angular velocity of 8 rad/s what is the flux (ΦB)at any time t? Remember that this means the angle that the plane of the loop makes with the B field can be described by θ = ω * t where ω is the angular velocity. You will need to make a careful drawing to be clear.
Assignment: HW Flux
Turn in all the problems for HW Flux in the LMS
Assignment: Reading
Go on to Faraday II breadcrumb for the cool consequences of these ideas.
