Mood Brightener: ...more from Stay Homas. (Confination XVI)

Magnetic Forces:

Conceptually it is clear that magnetic forces share a remarkable number of characteristics with electrostatic forces. On the other hand it is tough to sort out the force rule in the same way we did for charges because we can never get ahold of an isolated N or S pole. We could work to see if the interaction between magnets has the same mathematical form as the interaction of 2 electric dipoles. This has many complications but it is arguably doable.

The other approach is to begin with the idea that there is a field around the magnet that looks like the field around an electric dipole and study how charges interact with that field. Because the magnetic field and the electric field clearly operate differently we need a different name. The magnetic field is usually labeled B (not M as you would expect).

Interactions of charges with a B field:

Think for a moment how we will do this.....

Observations:

1: Only moving charges seem to feel a force (greater v means greater force)

2: Bigger charges feel bigger forces.

3: Same charge in a bigger B field (kickier magnet) feels a bigger force.

So what is a mathematical rule that you would write down to capture these observations?

• F_B=qvB

The only unresolved question is the direction of the force. For F_E the force on a positive charge is in the same direction as the E vector. Here is where the observations get really interesting...

4: The magnitude of the force depends on the direction the charge is moving. It varies between 0 when the charge is moving parallel to the B field to a maximum value when it is moving perpendicular to B.

5: The direction of the force is perpendicular to BOTH the B field AND the direction of motion--sheesh!

This takes some thinking but when you get to MTH 254/255 you will find out about the vector cross product which has these same characteristics -- a freaking miracle!!

I usually prefer to write it this way:

which helps me keep track of what the angle means.

Right Hand Rules:

There are many but lets look at a few before we go do it the way we do it in math and physics....

 

 

 

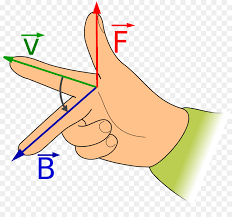
These are inconsistent and awkward. Here is how the physics and broader math community do it.

 

 

Negative Charges:

So what about negative charges? The totally reasonable expectation would be that (-) charges do the opposite of (+) charges. That does indeed turn out to be the case so how do we track this when using the RHR? The general advice is to apply the right hand rule as usual and then flip your thumb over 180^o to get the direction of the force on a (-) charge. I will reluctantly say that you could use your left hand for (-) charge but don't. It generates more confusion than anything else to try to have a different rule for each sign of charge.

As an example: Let's say you have a B field pointing directly West. A (+) charge moving directly upwards will feel a magnetic force to the South. A (-) charge moving directly upwards (same direction) will feel a magnetic force pointing N.

Units:

So what are the units of B? How about we look at the force expression and see what it tells us. Take a moment and figure it out before looking ahead......

B is N/(C m/s)
There are two standard units that we use to measure magnetic field. The Tesla (named for Nikola Tesla) and the Gauss (named for Carl F Gauss). A Tesla (T) -- I know it looks like temperature -- is a N/(Cm/s) and is a robust unit of measurement. An MRI machine which has one of the strongest magnets you're likely to meet creates a field of about 15 T at the patient. This means most fields you meet with be typically mill, micro, or nano Tesla. A Gauss (G) is scaled to match our physical world a little better. The earth's magnetic field is about 1 Gauss (often a little less but close) at the surface of the earth. When we use the force equation in SI units we must express the B field in Tesla. The conversion from Gauss to Tesla is 10⁴ G = 1 T. Depending on how you look at it this means the Gauss is a really small unit of B field or Tesla are a really big unit for measuring magnetic field.

Note: Because of the relationship between electrostatic and magnetic units it is not trivial to check units in magnetic calculations and many people just express the B field in T and let it go at that. Be careful if you do so since checking units is a useful way to be sure you're on the right track.

Assignment Breadcrumb Reading: Bb Test

Why No Force Law Between Magnets:

All the other times we've started talking about forces we began with a rule describing the forces between sources of that force. F = mg, F = kqq/r2, F = -kx, and so on. Why not in the case of magnetic forces?

Before Next Class:

Assignment HW: Bb Test

Magnetic Forces/RHR #1:

An electron in an old school TV is travelling horizontally at 7.2.10⁶ m/s in a horizontal magnetic field of 83 mT. What is the minimum force the electron could feel in this field? What is the maximum force the electron could feel in this field? What are the possible directions for the force on the electron under these circumstances?

Assignment HW: Bb Test

Magnetic Forces/RHR #2:

Take a location on the earth where the magnetic field of the earth is horizontal and has a magnitude of 2.5.10^-4 T and is pointed straight North. If 1 C of negative charge (electrons) is traveling through a wire headed either East or West how fast must the charge be going, and in which direction if the magnetic force exactly balances the gravitational force on a Coulomb of electrons?

Looking Ahead:

Look ahead to the next Breadcrumb: Magnetic Force II

Assignment Breadcrumb Reading: Bb Test

Gyroradius:

What is the minimum gyroradius for a proton moving at 500 km/s (a typical speed for protons from the sun when they reach the earth) in the earth's magnetic field of 50 μT?