1) The nucleus of a He atom contains two protons separated by an average distance of 3.0^.10^-15 m. What is the magnitude of the electrostatic force that one proton exerts on the other at this distance? What is the 3rd law pair to this force? If this is the only force acting on the proton what is the acceleration it would experience? You will need to find the mass of the proton and use some physics from PH 211 to figure this out.

2) Two small balls are given charges of opposite signs. The charge on one ball is twice that of the other ball. They each feel an electrostatic force of 14 N from the other. The magnitude of the smaller charge is 7 mC. How far apart are the two balls?

3) Two identical insulating blocks are given the same net positive charge on one face. Each block has a mass of 1.5 kg. When one block is placed above the other (which sits on the table) it floats 2.5 cm in the air. Assuming you can treat these blocks as point charges how much charge is on each block? Do you think a freebody diagram would be helpful -- hint, hint!

4) Two small spherical water drops have charges of -1.0^.10^-16 C and a separation of 1.0 cm. What is the electrostatic force between them and how many excess electrons are there on each drop?

5) Four charges of magnitude 100 nC are arranged in a 5 cm square. One pair of opposite corners are positively charged and the other corners are negatively charged. What is the magnitude and direction of the force on one of the positive charges?

6) Two tiny conducting balls of identical mass and charge q are hanging from insulating strings of length L. Show that the separation between the balls when they settle to equilibrium is (in the small angle approximation) given by

7) Here's an application problem (sort of the inverse of #3) to consider. (I may or may not have shown you how to charge scotch tape by pulling it up off the table) If you create oppositely charged tapes they will attract each other. If you lay one tape sticky side up on a table and bring the other close above it you should be able to determine the distance at which the attractive Coulomb force exceeds the force of gravity on the tape. From this information, assuming that the charges are equal on the two tapes (why should this be?), and knowing that the mass of scotch tape is roughly 1 gram/meter you should be able to figure out how much charge is on each piece of tape. As a guide I find that the bottom tape comes up off the table when they are about 1 cm apart.

 

8) (Integration) A plastic rod 30 cm long (L) has a total charge of 5 mC (Q) uniformly distributed along its length. What is the force on a 10 mC charge located 10 cm (b) from the end of rod along the axis of the rod? Take the time to draw yourself a picture and work thoughtfully through the setting up process we talked about in class. Have fun -- we'll be doing lots of practicing on this stuff.

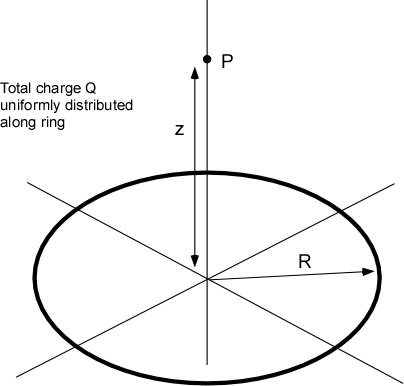
9) (Integration) A total charge Q (5 mC) is distributed uniformly along a ring of radius R = 6 cm. The ring lies in the x-y plane with it's center at the origin (see below) second charge of 10 mC is located at point P 20 cm up the z axis. Take the time to draw yourself a picture and work thoughtfully through the setting up process we talked about in class. Determine the force on the 10 mC charge from the ring of charge.

Answer Cloud:

[1.5^.nC] /[250 m]/ [5.6^.10³ N]/ [9.0^.10^-19 N, 625 e's]/ [small angle assumes cos = 1 and sin(θ)= tan(θ)] /[25.6 N => 15 ^.10²⁷ m/s² ]/ [51 mN]/ [1.0^.10^-6 C]