1) Three charges are spaced 10 cm apart along a line. They are +q, -3q, and +q respectively where q is 300 nC. Determine the magnitude and direction of the E field due to each charge midway between the +q and -3q charges (either one is the same setting). Determine magnitude and direction of the total E field at that point.
2) Three charges are placed on the corners of an equilateral triangle whose sides are 10 cm in length. The charges are -1q, -2q, and +3q respectively where q = 5 nC. What is the magnitude and direction of the E field due to each charge at a point midway between the -q and -2q charges. Determine the magnitude and direction of the total E field at that point.
3) A soap bubble (m= 0.05 g) has been given a charge of +5 nC. When it is placed in an E field it is found to float without falling. What is the magnitude and direction of the E field?
4) Four charges of magnitude 100 nC are arranged in a 10 cm square. One pair of adjacent corners are positively charged and the other corners are negatively charged. What is the magnitude and direction of the E field in the center of the square?
5) Consider a dipole consisting of a +q and -q separated by a distance “a”. the axis of the dipole is the line which runs through both charges. The center of the dipole is midway between the charges. Show that the E field a distance x along the axis from the center of dipole is given by
when x>>a (this is supposed to trigger an approximation!) and where p=aq is known as the dipole moment. Take the time to sketch this out clearly before starting the problem. It is NOT a calculus problem!
6) (integration) A line of charge extends from -L to the origin of the x axis. A charge Q is uniformly distributed along this line. Determine the E field along the positive x axis a distance “b” from the origin. (symbols, not numbers)
7) (integration) A line of charge extends from -L to the origin of the x axis. The linear charge density is given by λ = ax. Determine the E field along the positive x axis a distance “b” from the origin. (symbols, not numbers)
There will be two terms in your answer one of which is a ln() term.
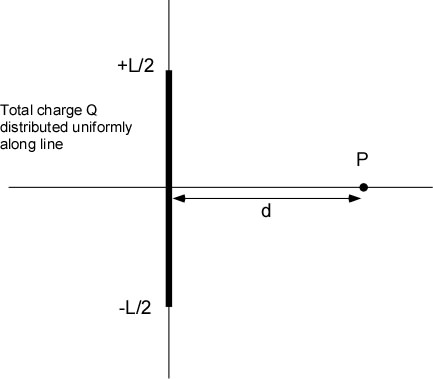
8) (integration) A line of charge is oriented along the vertical axis from -L/2 to + L/2. A total charge of Q is uniformly distributed along the line. Point P is a distance d along the horizontal axis from the center of the line of charge. Determine the total E field at P.
Bonus! (integration) A total charge Q is uniformly distributed over the outer surface of a hollow cylinder of radius R and length L. The center of one end of the cylinder is at the origin. Point P is a distance z away from the origin. Determine the E field at P. Hint: Slice the cylinder horizontally into rings and use your results from the last problem of the previous problem set to set up your integral.

[kQ/[b(b+L)]]/[4.2.106 N/C towards -3q/[5.0.105 N/C]/[ka{ln((b+L)/b) + (L/(b+L))}]/[2.4.104 N/C at 45 degrees wrt side of triangle]/[1.0.105 N/C]
