SHO: Simple Harmonic Oscillators
Getting the Differential Equation:
-
Make a decent sketch of the problem and verify that it seems likely (due to a restoring force) to actually oscillate.
-
Determine whether the oscillation in linear or angular and label the coordinate system in which the oscillation takes place. Get out Newton's 2nd Law in it's appropriate form and write it down!
-
Construct a most excellent freebody diagram which allows you to determine all the relevant terms for the Force or Torque side of Newton's 2nd Law.
-
Rewrite Newton's Law as a differential equation with all term on the same side of equation and see if it matches the standard Simple Harmonic Oscillator form shown below;
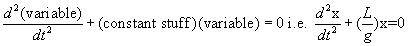
-
If equation is in this form then you write down the solution:
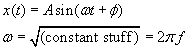
-
If equation is not in this form it is usually because the linear first order term is not linear. It is likely that you will now be expected to attempt some form of linearization often through the use of a small angle approximation. If you have trigonometric terms then see if it is reasonable to assume that the angle of oscillation is small and then consider replacing cosine( θ ) with 1 and sine( θ ) with ( θ ). If this then linearizes your equation then go back to step 5 and finish.
-
If you still don't have an appropriate equation then complain to your instructor or learn more advanced techniques for solving differential equations.
