Damped and Driven Motion:
What we have considered for the time being is ideal periodic motion. It's been ideal in a number of ways and one of those ways is the idea that the pendulum or the spring system will go on forever without stopping. Clearly crazy given that there are always frictional forces at some level.
Damped Periodic Motion:
Ultimately damped periodic motion is about energy loss. The amplitude of the periodic motion is a reflection of the energy in the system (why?). Let's consider a particular system shows all the typical mathematical features and is pretty understandable. The video clip is pretty clunky because I made it on my kitchen counter because I couldn't find a decent one on Youtube. (2020) I still can't find a good video on line anywhere so you are stuck with this awful video for now.
Activity: Now, make a complete freebody diagram of the bottle as it bobs in the water. Be careful about choices of coordinate direction. Get to the point where you have Newton's 2nd Law written down for the vertical direction.
As you are working on this activity here are some useful (maybe) comments and added information.
Fg: Does it change magnitude or direction during the problem? If so, what does it depend on?
FB (the bouyant force):
Do you remember the expression for the bouyant force? Is it in the + or - direction in your coordinate system? Does it change magnitude or direction during this problem? If so, what does it depend on?
Depends on mass of water displaced which on depends on the depth in the medium - y.
Fdrag (fluid drag force):
Fdragis a tricky one since it is very much like a force of friction except that this time we are not talking about rigid objects like we did in PH211. In fluids the drag force tends to depend on the speed of the fluid relative to the object (think of putting your hand out the window of a moving car).Does this force change magnitude or direction during this problem? If so, what does it depend on?
Generally depends on v2 but at low speeds only v
At some point we will have to decide on a physics model for the drag force. At low speeds we can generally assume it is linear with speed moving to a v2 dependence at higher speeds and something totally different at very high speeds where we have turbulent flow. If you want to dig deeper into this as some of you will in your projects the Wikipedia article on drag is actually very good.
From Newton's 2nd to the DE for damped periodic motion:
Here is a summary of what I hope you found in your group work.
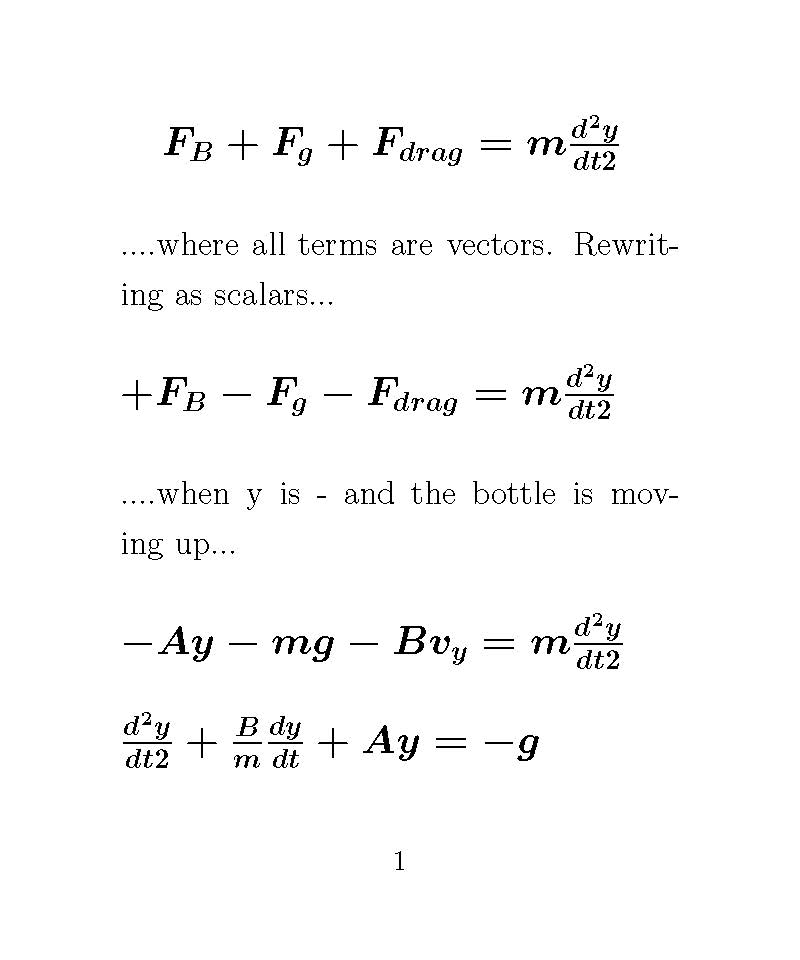
A and B are unknown constants that depend on the shape of the object and the drag coefficient between this particular fluid and the bottle.
Here is a link to a video from MIT OpenCourseWare for the equivalent of PH213. The particular demo that would be helpful to see starts at 48:45 in this video. This demonstration compares the periodic motion of a simple spring system and one with a substantial 'hat' that creates a significant drag force. This leads to the same general form of the equation we have been looking at. If you are moved to do so you can start the video at 33:30 and watch Dr Lee explore the entire mathmatical derivation for a damped spring system.
HW: Damped
Given the differential equation for a damped harmonic oscillator below show that the proposed (thoughtfully guessed) solution actually works and satisfies the equation. This is another example where I am asking you to use a trial function with a number of undetermined constants. When you 'put the trial solution into the diff eq' you will find (algebraically) that the equation can only be true at all times if the constants have particular values (see b and ω below). You will find that there are no constraints on C (the amplitude) or φ, the phase shift.
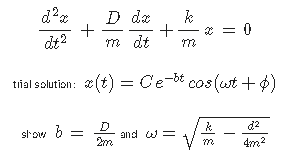
HW: Damped
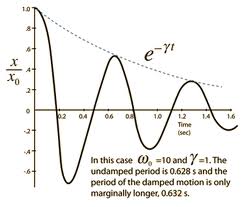
The following plot shows an object experiencing damped periodic motion. Assume that the vertical axis is labelled in m. Estimate the maximum velocity at each succesive point where the curve passes through the equilibrium point. Use the tools we have developed for well behaved periodic motion. You should be able to get 5 data points off the plot. For each one determine the kinetic energy of the 100g mass which this plot represents. (do so!). Is the loss of kinetic energy constant from peak to peak? Can you tell if the rate of change of the kinetic energy is a constant percentage of the previous data point?
Driven:
You will not be surprised that Driven Periodic motion is, energetically, just the flip side of damper periodic motion. The mathematics of a time dependent force added to the differential equation are a bit different and I don't know if you will explore that system in MTH 256. We will only explore it conceptually here.
Here's a clip of the upper deck of RFK Stadium in Washington DC the week after we covered this in class. First 6 sec are a short loop when the fans were in sync and the second 6 sec shows what happens when fewer are participating and they are less in sync. It was pretty exciting to be standing almost underneath this event knowing that they were going to close and demolish the stadium within a few months.
A more spectacular version of this same behavior is shown in the video below...
How would you expect that we would go about trying to figure what is going on? ...you'd be right, Newton's Laws. The issue of course is that this is a very complex physical object that is a challenge to model.
Simple Physical Model:
Think about your youthful experiences on a swing. In the begining someone else provides a periodic external force called a driving force that adds energy to your motion. It may seem obvious but they add energy at particular regular intervals unless they are doing 'Underdogs'. If the parent pushes the child at random times the whole experience doesn't work out well.
Now think about how you learned to pump yourself on a swing...how exactly do you do that? When you see very young children trying to learn this at the park they often push themselves back and forth in the swing seat very rapidly which doesn't work. What you eventually learn is that when you lean forward and when you throw yourself back is important. Like the parent you have to add energy at the right time.
What is the relationship between the period of the pushing force and the natural period of the swing?
The core concept is that when the period or frequency of the periodic force which adds energy is the same as the natural frequency of the system then energy is added very effectively. This is called resonance. It turns up in the differential equation as a time dependent term on the right hand side of the equation. It does not usually depend on the position of the object.
Activity: How do these ideas apply to the two videos posted above? Why do you think the stadium held together and the bridge failed?
Damped AND Driven:
All real periodic systems have at least a tiny bit of damping in them. Driving forces come in a whole lot of different forms. When both processes are taking place simultaneously the balance between the amount of energy added and removed is critical. In the stadium video, once the deck got moving a little, the energy being removed by the flexing of the deck was matching or exceeding the energy added by the bouncing fans. In the Tacoma Narrows bridge video the energy being added to the periodic motion exceeded the energy removed until the bridge was moving violently. At that point the energy in and the energy out were pretty closely balanced but that meant the bridge kept swinging dramtically until the materials of which it was made failed. This is not the only bridge in the world to have this happen.
Here is a clip of a recent example, London's Millenium Bridge, which had a lateral resonance generated by the peopl walking across it on opening day. Pretty impressive motion driven by pedestrians adjusting their walking to compensate for the motion and inadvertantly adding energy to the resonance at just the right rate.
Here's another fascinating version of damped and driven periodic motion. What provides the damping (energy removal) and what is providing the driving (energy addition)? Given that so many resources for physics are delivered by older white males this set of videos is an interesting exploration of some diversity. This first one is white and male but definitely young. The second is white but young and female and a good connection to Physics Girl who has a number of good videos I hadn't found before. The last is a team effort though unfortunately uniformly white. Other diversities that may exist are not detectable from this side of the flat screen.
It can be done by adults as well....
..and sometimes having the tech doesn't solve everything.....
Why does the glass NOT shatter if the pitch you are singing is not exactly right? If you decide to attempt Chase's trick please wear safety glasses since he was a little lucky that he didn't get damaged by flying glass. There are many other videos of this physics demo out there so be careful not to get sucked down the rabbit hole.
Earthquakes and Buildings (and Bridges as well):
Buildings have natural frequencies as well and we will talk about them more when we get to standing waves. The same general concepts apply. The frequency or period of the driving force must be a pretty good match for the natural frequencies of the building. The Willis Building (formerly the Sears Tower) in Chicago can sway as much as 1 m from side to side when wind blows steadily a the right speed so the vortex frequency matches the natural frequency of the building. I couldn't find an actual video of the movement of the Willis Building (really?) but here is a video from folks who help tall building designers avoid problems like this. Notice that they are using a simulation program (our projects on steroids) to do the modeling.
For context here is a video from Tokyo (I think) during the 2011 earthquake. Nothing failed but it is still impressive to see buildings like these move like trees in the wind.
Assignment: HW: Damped
Turn in the various (2) homework problems in this breadcrumb.
Assignment: Reading
Go on to Wave Basics breadcrumb to move to our discussion of the kinematic characteristics of traveling waves.
