More than One Wave: Beats (on the way to Doppler shift)

What happens if we have two waves with different frequencies passing through the same part of space? Address this qualitatively by sketching two sound waves with different frequencies which are arriving at your ear with their crests in synch. Predict what happens if you allow time to elapse until one of them has the next crest arriving at your ear? Where will the crest of the other wave be at that moment? What does this do to the collective sound your ear receives?

Experience Beats:

Here's an online tone generator that you can use if you have speakers on your computer (Thanks to Paul Anderson of Bozeman Science for pointing this resource out!). Open up two tabs and play two different frequencies at the same time. Does this match what you expected?

How would you write down the mathematical starting point for this situation (how do you express two waves of different frequency moving in the same medium?)

Here's an animation from our friends at Penn that will give you a visual sense of what you've been playing with as well as showing you the starting and ending points for the math.

Beat Frequency:

f_beat = |f₁-f₂|

Musicians use this effect to help them tune. Can you explain how? Use the tone generators to explore what happens when pitches (frequencies) are very close to the same. Note the key strokes that will let you make the pitches very very close to the same. Be sure to play each pitch separately and notice how difficult it is to tell them apart yet when you play them together it is quite obvious that they are not the same. Does it work that same when the 'base' frequency is 3 kHz (besides being more irritating)? What is the precision of this measurement that you are doing with your ears if the pitches differ by just 1 Hz?

Now explore frequencies that are quite different. A particular example that might be valuable to try is f1 = 440 Hz and f2 = 660 Hz. This is actually part of a chord that is generally pleasing to western ears (root and 5th of a chord). What do you hear? What does the expression you wrote down earlier predict for the beat frequency? How is this related to the 440 Hz? Adjust the loudness of each frequency until you can hear it. What does this mean for musicians? This relationship between notes is the same as the fundamental frequencies of adjacent strings on mnay instruments.

If sound waves can produce beats that we hear as other sounds can light waves do the same thing? Look up the frequencies of visible light and consider whether this is possible.

HW: Doppler

I have three tuning forks (A, B, and C) which produce slightly different frequencies. When A and B are sounded together a 2 Hz beat frequency is heard. When A and C are sounded together a 5 Hz beat is heard. What beat frequency will be heard when B and C are sounded together? (there are two answers!)

Now, Doppler Shifts:

Just to be clear, this concept of Doppler shifts was applied to a simple problem from astronomy in the last 50 years and the results completely disrupted our understanding of the universe. Doppler shifts in the light coming from galaxies created the need for dark matter and dark energy. Not bad for a simple idea.....

Using Your Tools:

Remember that my point this term is to have you work on your problem solving skills and how you approach real problems where you don't know the answer.

Start by drawing a speaker on wheels which is stationary pointing towards a stationary (for the moment) listener. Be generous with your labels. Draw the location of the first 3 or 4 crests of the sound wave headed towards the listener. What frequency will the listener hear? Why? Before we move onto the next part be clear in your mind about how our ears detect sounds and how that relates to the wavelength, frequency, and speed of the sound wave.

Activity: In your groups you will follow through the steps given below to arrive at an expression for the wavelength the listener experiences compared to the previous version of the setting. I expect this will take some time.

Now, on the same drawing, show the speaker moving towards the listener as it is 'pumping out' crests. You are likely to find that you need a few more labels on this drawing. Where will each of those new crests be relative to the ones you originally drew? What is the new distance between the first two crests that arrive at the listener in this new scenario? What is a mathematical expression that relates the original wavelength to the new wavelength and the motion of the speaker?

Since what we actually detect is frequency of the sound how do you turn this statement about wavelength into a statement about the frequencies that are being produced by the speaker and detected by the listener?

 

[insert video here]

Self Reflection:

It is my experience that, even though you have all of the tools from PH211 needed to figure out the previous relationship, it is significantly challenging. Why is that? What is it that is difficult about using tools you know in a different setting?

Activity: In your groups redo your sketches and consider the question of the observer being in motion. In the previous case it was conceptual more direct to consider the impact of the motion of the source on the wavelength of the wave. In this case (hint) it's easier to consider the impact of the motion of the observer on the period between successive crests.

[insert video here]

In the end both of these expressions can be combined into the following mathematical tool that deals with either or both the source and the observer being in motion.

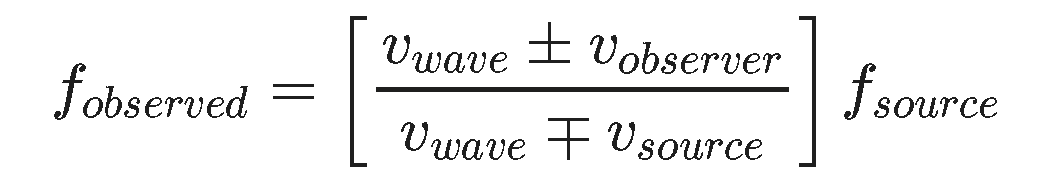
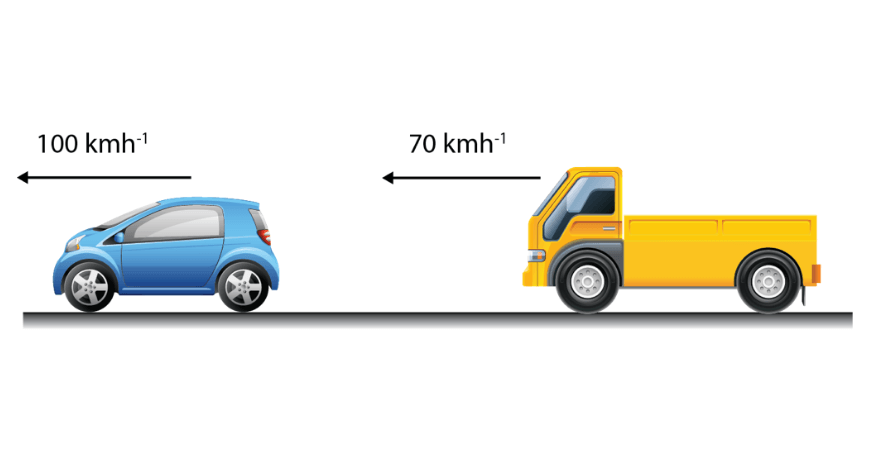
The plus/minus signs are written specifically the way they are to allow us to note that motion of the source TOWARDS the observer or motion of the observer TOWARDS the source means you use the TOP sign of the two. Be cautious to recognize that this motion is describes what is trying to happen not the ultimate relative motion of the source and the observer. Consider the setting below where the truck is chasing the car but the car is getting away. If the car blows it's horn and we ask what the driver of the yellow truck hears then the truck is the observer and the car is the source. Because the truck is moving towards the car, even though it's falling behind, I use the + sign in the numerator AND the + sign in the denominator because the car is moving away.

You will sometimes see different language for this expression where the following substitutions are made...

Not surprisingly I prefer my notation for it's clarity about the terms represent.

HW: Doppler

What happens if you are a bat flying at 7 m/s at an stationary object which reflects the sound back to you? There are two doppler shifts here. The reflecting object sends back the frequency that it 'observers' for the bat to become the new observer. Assume the bat emits a frequency of 40 kHz. What is the frequency that the bat observers coming back to him?

HW: Doppler

Astronomers observe the red light (656 nm = λ) from hydrogen using spectrometers. This light is observed to be redshifted (moved to longer wavelengths) in most astronomical objects. If the galaxy is receding from us at 25% of the speed of light (speed of light = c =3^.10⁸ m/s) what is the wavelength of red light that we will observe? You will need to convert the Doppler Shift equation to a wavelength equation before doing this problem

Assignment: HW: Doppler

Turn in the various (3) homework problems in this breadcrumb.

Assignment: Reading

Go on to the Doppler Shift II breadcrumbs where we will look at a variety of more complex applications