Doppler Shift: Applications

Relative Speed vrs Source and Receiver:

It is natural to wonder whether we really have to consider the individual velocities of the source and the observer when it seems like the relative velocity is what should matter. Let's look at a couple of cases.

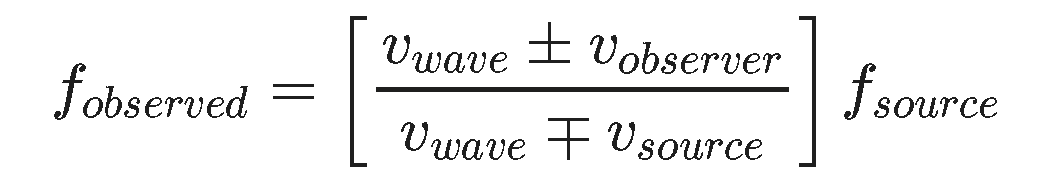
Both Source and Observer Traveling in the same direction at the same speed:

In this case the signs top and bottom must be the same regardless of which is the observer and which is the source. This means that everything inside the square brackets is just 1 regardless of how fast they are going except when they get to the speed of the wave. If they are both moving at the speed of the wave and the observer is moving AWAY from the source then both of the signs are negative and we end up with 0/0 inside the square brackets. What does that even mean? Why doesn't happen when the observer is moving TOWARDS the source which is running away at the speed of sound?

There is no frequency shift if the relative velocity of the source and receiver is 0 which is what you would get if they were stationary. This makes it seem like the relative velocity is whats important.

Source or Observer moving at v_wave:

Imagine that the source is moving AWAY from the observer at the speed of sound. This leads to the observed frequency being reduced by a factor of 2 [v_wave/2v_wave]. Now change the problem so the observer is moving AWAY form the source - same relative velocity. If the observer is moving at the speed of the wave the waves will never get to the observer and there is no frequency. A very different outcome!

Source or Observer moving slowly relative to v_wave:

Let's repeat the previous example but with the speed of the source or observer being 5% of v_wave. Quickly running the math I get f_o = .95 f_s when the observer is in motion AWAY from the source. I get f_o = (1/1.05) f_s = .952 f_s when the source is moving AWAY from the observer. Very close though not perfect. Why is this? To answer this we need to revisit a topic from power series......

Geometric Series for (1+x)^-1:

The geometric series for (1+x)^-1 is given by:

(1+x)^-1 = 1 - x + x² - x³ + x⁴ - x⁵ +....

IF x << 1 (otherwise known as 'x is small') then

(1+x)^-1 = 1 - x

...with high precision

So.... we can rewrite the Doppler Shift equation this way by dividing through by v_wave everywhere to get....

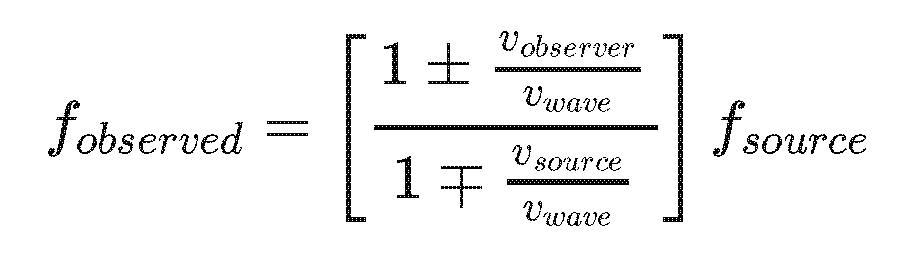
... assuming that the observer and/or the source are moving slowly compared to the speed of the wave we can apply the geometric series approximation to get....

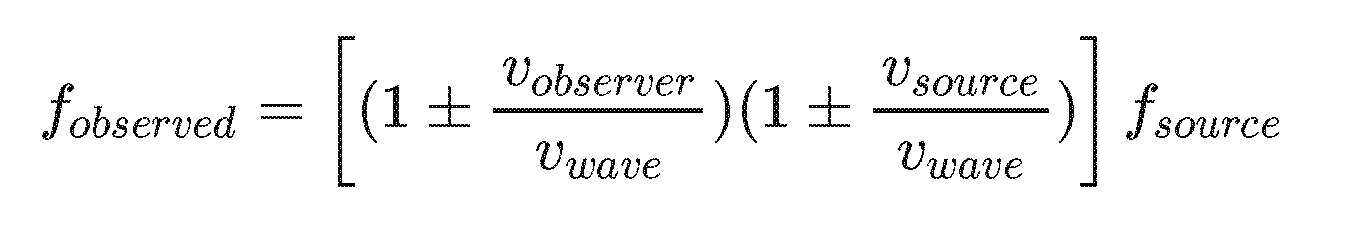
Which will give us the same result regardless of who we argue is in motion.

Take Home:

When the source and/or the receiver are moving at speed that are small compared to the speed of the wave we can determine the doppler shift from their relative motion with only a small loss in precision.

Bats and Moving Targets:

What if everybody is moving and there is a reflection in the middle of the process. This what a bat must do when it's hunting a moving insect. Lets assume the bat is moving at 7 m/s and the insect is moving at 3 m/s towards each other. There are two problems here -- what the insect receives and reflects back (due to both of them moving) and what the bat receives after is reflected by the insect.

Activity: Start by discussing which velocities goes where and what the signs should be using the standard (not approximate) version of the Doppler shift equation. Once you have agreed on those then decide whether it's reasonable to use the approximate equation based on relative motion. Which terms remain and what signs should you use this time?

Police Radar:

I know that the police now have access to laser speed 'guns' but the traditional tool of the police force is a microwave source and the doppler shift equation. If the police are standing still using the microwave source the problem is a little like the bat problem on the previous HW. If both the police and you are moving then the problem is like the moving bat and insect problem above.

What is the speed of the wave in this case? Are we justified in using the approximate doppler shift equation? If the microwave gun has a source frequency of 2.1 GHz what is the change in frequency you expect when you are drive at 35 m/s towards the 'radar' gun?

Beat Frequencies:

To measure the frequency of the returning microwave requires a ridiculous level of precision that is actually not possible. What if I were to 'mix' the source wave and the returning wave together --- what would happen? Can you say beats! The beat frequency measures the difference between the frequencies of the two waves. The beat frequency is around 1-2 kHz which is an audio frequency that I can easily measure with a tuner app on my phone. This is how it's done.

HW: Doppler Applications

As I drive down from Mt Hood my entire instrument panel in the car fails along with my brakes. As a accelerate down the winding road I wonder what to do. In desperation I lay on the horn which happens to produce a pitch I recognize as 392 Hz. Instead of calling to police in response to my obnoxious behavior the person in the identical car parked along the road blows their horn (also at 392 Hz due to manufacturing consistency) in a futile gesture of solidarity. The combined effect of the two horns produces a beat frequency of 60 Hz which I hear as a low pitch. As I hurtle towards my fate I frantically calculate my speed based on the beat frequency and Doppler shift ideas. What speed do I calculate?

HW: Doppler Applications

Suppose bats have a social need for police to enforce a speed limit because too many teenage bats are crashing into trees that they could have avoided. A Bat Patrol (BP) is formed and is trained to use doppler shifting of their squeaks to determine bat speeds. Officer Barney (BP 302) observes that the reflection of his calibrated (40,000 Hz) squeak from Tony Teenbat is up by 3500 Hz as Tony approaches him. Barney is flying at his normal cruising speed of 4.5 m/s. What is Tony's speed?

Galaxy Rotation Curves

This is an image of M31 (otherwise known as the Andromeda Galaxy). From it's shape and structure you would reasonably expect that it is spinning. That means the light from stars in the top left of the image is from sources that are moving towards (?) us and the light from the stars in the bottom right are moving away from us. We should be able to measure how fast using the doppler shift.

We do this by looking at particular lines in the spectra of the light from those stars. If they are coming towards us they should be 'blue shifted' and if they are going away from us they will be 'red' shifted. The individual lines are from the absorption/emission spectra you studied in Chemistry. Are the spectral absorption lines in this group of galaxies blue shifted or red shifted?

That's the concept now here's what the data looks like....

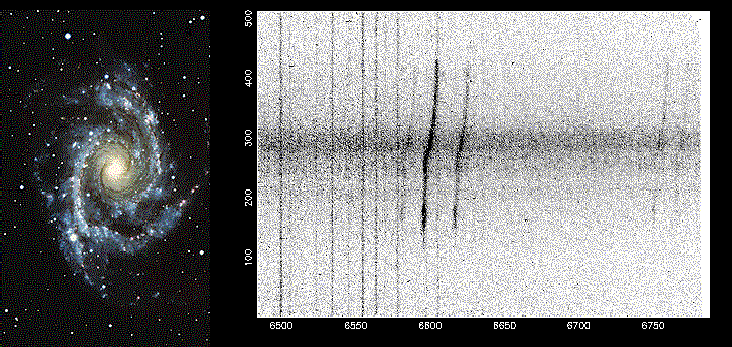
Which side of the galaxy is coming towards you and is the data consistent with the image? Are stars halfway between the center and the edge moving faster or slower than the ones on the edge? Since we believe we understand gravity pretty well here's what we would predict for the rotation curves for a galaxy like this one. The dotted line is what we predict and the dark line is what we see over and over again.

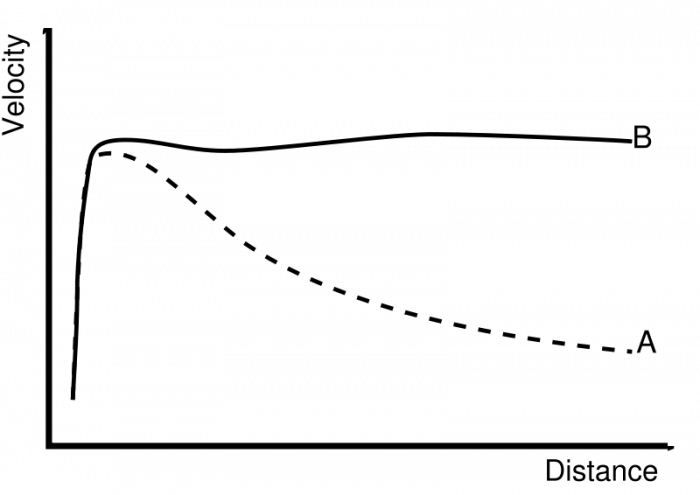
The basic story is our prediction is pretty terrible and the answer we have developed is that there is something dark out there we can't see that's making gravity. Trust me......

Lastly...Hubble Redshift:

If we look at galaxies as a whole and don't worry about their rotation we can see that overall their light is shifted towards the red from where we expect the spectral emission and absorption lines. The earlier image is an example. When Hubble looked at data from galaxies where we had some sense of the distance to that galaxy here is what he saw in the data. This immediately raises the question of why. An important feature of this data is that it doesn't matter what direction you look all the other galaxies seem to be running away from us. Huh?

 

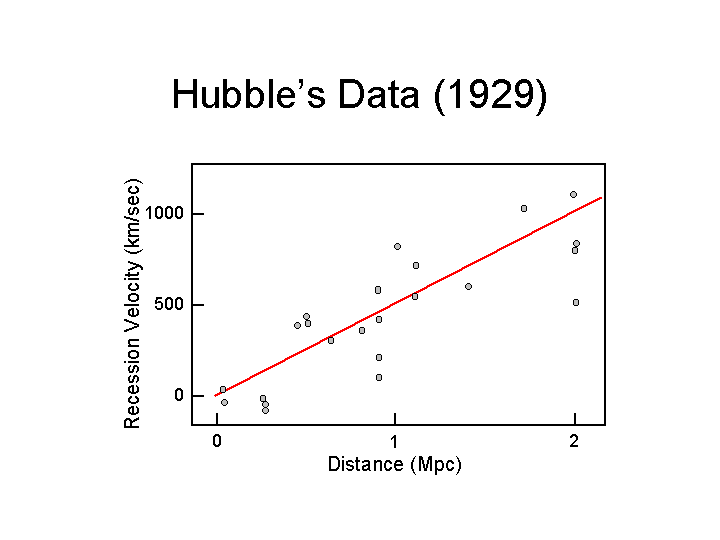his.

There is a whole discussion about how this led to our understanding that the universe is expanding and why that might be. It also explains why, as we look further and further away into the universe, we have to use infrared detectors to see the most distant galaxies because their doppler shift has moved them completely out of the visible part of the spectrum. We now use the redshift of a galaxy as a proxy for the distance it is from us. Here is what a tiny slice of the universe looks like if we plot where all the galaxies are along a narrow slice of the sky.

Map of galaxies based on redshift

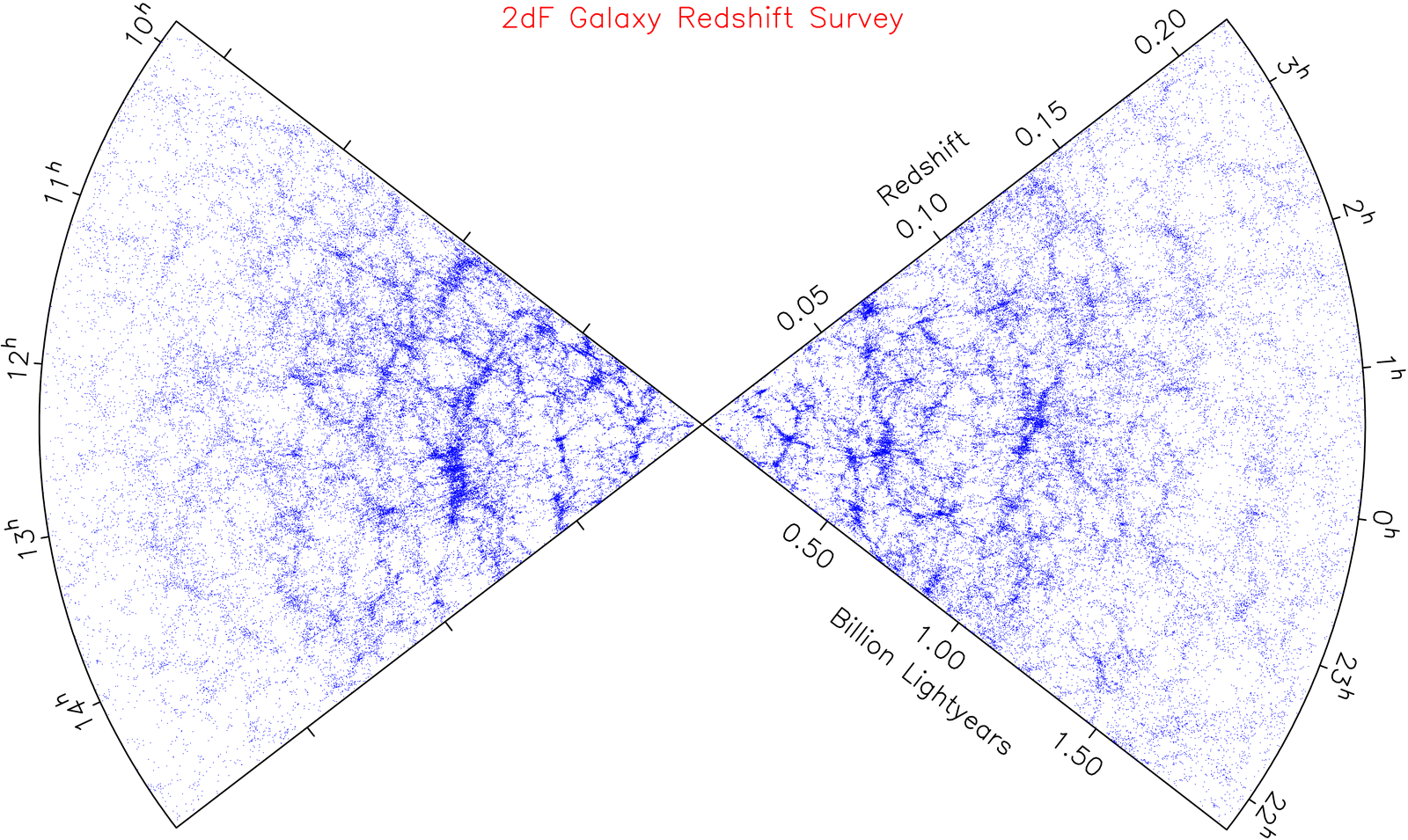
Why is there a gap in this data vertically through the middle?

HW: Doppler Applications

Here's another example that needs you to consider the data and be sure you understand how to use it in this context. Here is some real data starting, at the bottom, with a star which is NOT moving relative to us. Determine how fast each galaxy is moving and whether they are approaching or receding from us. In case you are wondering the things to the left of the spectra are the galaxies starting with the most distant at the top. You will need to wavelength version of the Doppler Shift equation for this problem but luckily you figured it out last time.

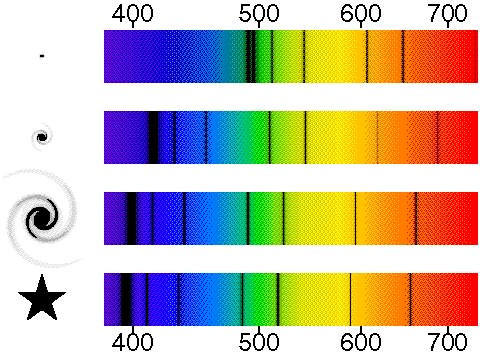
Assignment: HW: Doppler Applications

Turn in the various (3) homework problems in this breadcrumb.

Assignment: Reading

Go on to the Interference breadcrumb to get us started on another cool wave behavior!