Light and Other Conundrums:

What does a wave do that other 'creatures' don't? How would you check to see if a phenomena is or isn't a wave? Interference is a behavior which is fundamentally about waves. As we saw in our previous discussion of interference light shows this behavior (see the Veritasium video)

Maxwell and the Wave Equation:

Maxwell's Law and their relationship to the wave equation for light is a delightful and complex mathematical journey and I am often tempted to reproduce it for you. More rationally, what you need at this point is a more conceptual perspective on the complexity of light so I have created a separate breadcrumb for those interested in a deeper exploration of Maxwells equations and how they lead to a wave equation for EM waves. For now here is the basic perspective I'd like you to internalize. The first equation is a version of Gauss' Law arises from Coulomb's Law and basically asserts that charges lead to E fields. The second equation recognizes that B fields arise from dipoles and there are no magnetic monopoles. The third equation is just Faraday's Law in another form - E fields arise from changing B fields instead of describing voltages from changing flux. Given the symmetry between of the first two equations it should be no surprise that there is an equation equivalent to Faraday's Law connection magnetic fields (H) and changing E fields. This we did not study but is called Ampere's Law.

Image from Asem Elshimi

Here is a very nice conceptual discussion of Maxwell's Laws (thanks PBS!) and its relationship to EM waves which travel at the speed of light. This is what led us to realize that light must, at least in some sense, be an EM wave. Notice that the wave meets our definition of a transverse wave.

The take home message? The take home message is that long slow development of our understanding of these mysterioius things called E and B fields had hidden within it the mathematics of a wave that combined the E and B fields. This wave has a speed of c = 3.0 ^. 10⁸ m/s which matches the observed speed of light. From Maxwell's derivation we also find that the E and B fields must be perpendicular to each other as illustrated in this animated gif.

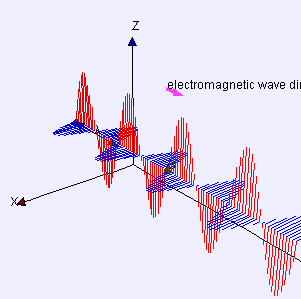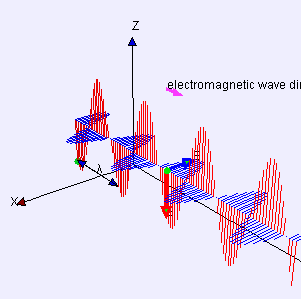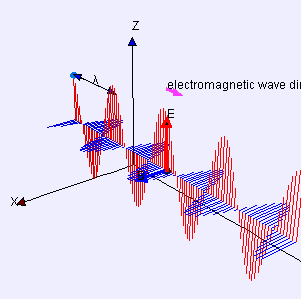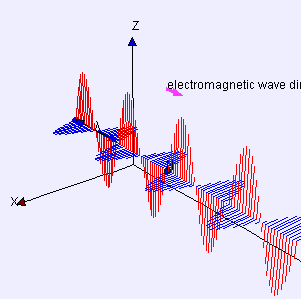
Light is a Wave!

It is often confusing what this sine function represents. Here is a pretty nice visualization of the relationship between the plane wave (E field only) and sine function shown above that we use to represent it.

Image from BMS on physics.stackexchange

From the other perspective....what do particles do that waves don't?

Chemistry Connection:

To understand the effect we're about to explore we need to revisit a topic you may remember from your chemistry class -- the emission spectra of atoms. There is a lot that goes into this but suffice it to say that atoms emit or absorb light at specific wavelengths that are associated with transitions between energy levels in the atom.

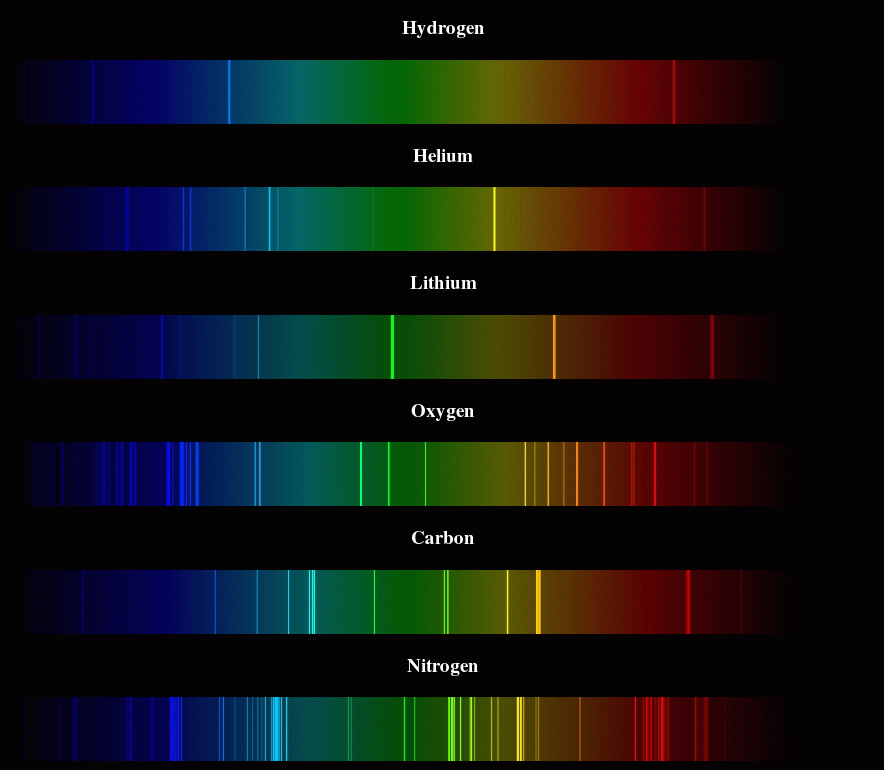
Particles deliver energy in chunks. A stream of particles is much like a wave in the sense that it adds energy continuously to a setting. Low amplitude waves deliver energy very slowly and high amplitude waves deliver energy quickly. The photoelectric effect is an experiment from the early part of the 20th century that was very puzzling for physicists because the results don't align well with the idea of light as a wave. In the video clip (same wonderful teacher who made the Jelly Baby wave machine!) the UV light source is in the blue tube and is emitted through a hole in the side that you can't quite see.

 

The explanation for the photoelectric effect is what Einstein actually got his Noble Prize for. What is puzzling and important in the demonstration is that visible light will never release an electron from the zinc plate allowing the the electroscope to discharge. No matter how bright (high energy) the light is nothing happens. UV light, on the other hand, can be turned down so low that it is hard to detect and the instant it shines on the zinc plate the electroscope starts to discharge. To be more detailed, the wavelength of the UV light had to be shorter than a particular value for the electroscope to discharge. This was called the cut off frequency or wavelength. Einstein's great insight, which built on similar insights from others, was that IF the energy of the light came in 'chunks' that were at least a big as the energy transitions in the zinc that would explain the results of the experiment.

From this you would also predict that replacing the zinc plate with other materials would lead to different cut off wavelengths and indeed it does.

Light is a Particle!

How Much Energy?

The energy of a 'particle' of light is given by this expression..

E = hf = hν

..where E is the energy (in J) and f is the frequency in Hz. ν is another symbol for the frequency. h is the Planck constant which has a value of 6.63 ^. 10^-34 J-s. You will notice that an individual particle of light, called a photon, has a very small amount of energy.

Wave/Particle Duality:

It is important to appreciate that we are not actually saying light is a wave OR a particle. Light is some hitherto unknown creature which acts like a wave in some circumstances and like a particle in others. As it turns out, the same is true for electrons and protons. Since we can have no direct experience of light or an electron as a 'thing' it is hard to say what this unknown creature is. Worse yet, since physical objects are made of protons and electrons that must mean that we are also a version of this creature that is both a wave and a particle. You can definitely think of yourself as a complex superposition of many waves but I wouldn't advise trying to go through two openings at the same time and interfere with yourself. Relax and enjoy the confusion!

The Medium:

A very puzzling question about light is what is the medium that carries the light wave? This was a rich topic of discussion for decades as people tried to figure out how to detect and measure the expected medium. The Michelson-Morley experiment was a carefully designed experiment to detect this mysterious aether that carried the light. Part of what I love about the experiment is that they floated the whole experimental setup on a annular pool of mercury to isolate it from the rest of the world. In the end they found nothing and physics had to come to grips with the idea that light is the only wave we know that has no known medium. Even gravity waves have a medium if you think of the 'fabric of the universe' as a medium.

Light is the only wave that has no known medium!

Light and Momentum:

Since light, at least in some sense, is a particle carrying energy then, like other energetic particles, it has momentum. That suggests that some of our previous explorations of collisions and conservation of momentum should apply.

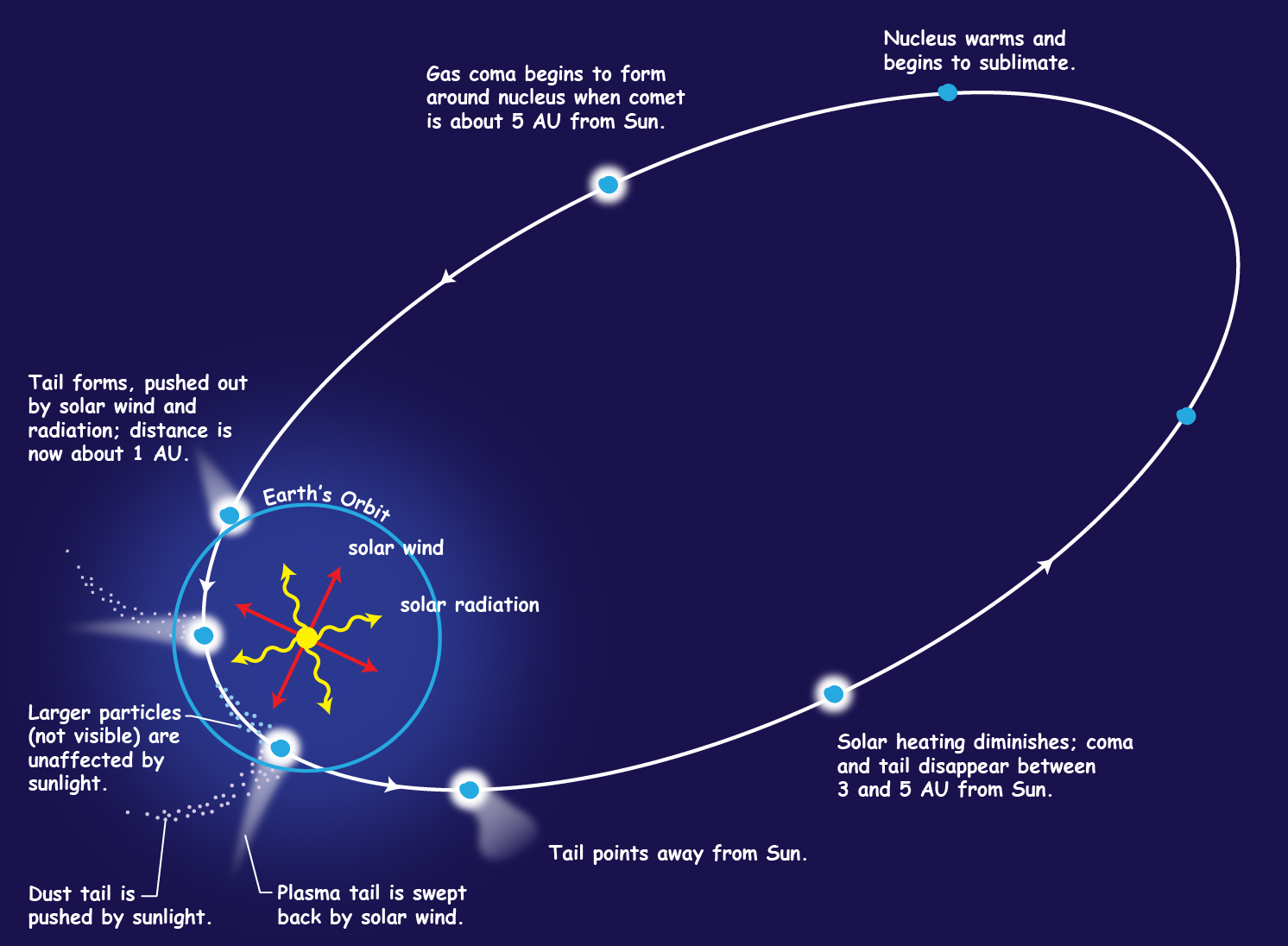
One of the most dramatic examples of this effect is the tail of a comet. As particles are vaporized from the comet the sunlight pushes them away from the sun. As the comet approaches the sun this all makes sense as the 'tail' trails the comet towards the sun. What is a little unexpected is that the 'tail' preceeds the comet (in 'front' of it) as the comet heads away from the sun. The momentum transfer from the sunlight to the particles in the tail of the comet provides the only plausible explanation.

The Poynting (pronounced 'pointing') vector is the name (symbol is usually S) which describes the energy delivered by light and is reported using units of W/m². The pressure delivered by that light is given by (in this image they use I instead of S!)

If you know the output power (in W) of a light source you can determine the Poynting vector by dividing the output power by the area across which it is spread. For central sources like light bulbs and stars the area is the area of a sphere at some distance from the source. The output power of the sun is roughly 4^.10²⁶ W and we at the earth are 1.5^.10¹¹ m from the sun. Running the numbers leads to a Poynting vector at the earth's orbit of 1416 W/m² which is what we typically use for the intensity of sunlight at the top of the earth's atmosphere. This means the pressure exerted an a shiny (reflective) object near the earth is 9.4 μN/m² . Not a whole lot but it can be significant as you will see in the HW problems.

HW: Light

A dust particle floating in space is subject to both gravitational attraction from the sun and radiation pressure pushing it away. The density of such dust particles in our solar system is 1000 kg/cubic meter. What is the diameter of a reflective dust particle that just balances the gravitational force from the sun with the radiation pressure at the earth's orbit? Is the diameter of such a particle dependent on the distance from the sun?

Crooke's Radiometer:

Watch first....I love that he poses the question but doesn't answer it. Once you've watched the video slow it down at around the 25 s mark and see which way the radiometer is turning. That will actually answer the question.

People have made better radiometers of this type and can, with powerful lasers, get it to turn away from the shiny side as you would expect from radiation pressure but it is not easy.

Space Sailing:

Radiation pressure has been proposed and tested as a possible propulsion system for autonomous satellites by multiple countries. Here's a link to NASA's solar sail testing a decade or so ago. As you might expect it takes BIG sails to get anything to happen and there are significant technical challenges. If you find this intriguing you might also enjoy Sunjammer, a short story by Arthur C Clarke, about a space regatta using radiation pressure to 'sail' a race. This was written as speculative science fiction in 1964 but the science is real and correct.

Lasers:

It has been proposed that radiation pressure could be used to push satellites through the solar system. This is because, ideally, laser beams don't spread out as they travel through space. The radiation pressure stays constant regardless of how far away the reflecting object is. A 5 mW laser (laser pointer) has a beam about 1 mm in diameter. That makes the Poynting vector S = 5 mW/π(1mm)² . Correcting for units this gives S = 1600 W/m². This is about as 'bright' as looking at the sun which is why it's considered relatively safe as long as you don't stare at the laser! That also means the laser provides a radiation pressure of 10.1 μN/m² on a reflective object (larger than the beam) at any distance. No doubt this will produce a tiny acceleration on some object but even tiny accelerations acting over long periods of time can lead to significant velocities.

HW: Light

A laser beam whose power is 4.6 watts (pretty kicky) has a diameter of 10 cm. It is directed towards the surface of a perfectly reflecting satellite in space with a mass of 50 kg. If the diameter of the satellite is greater than 10 cm what is the acceleration of the satellite and how long will it take to reach a useful speed of 10 km/s?

HW: Light

OSIRIS-REx is a satellite that just gathered a sample of the near earth asteroid Bennu. This satellite is roughly 3 m in diameter with a mass of 900 kg. It was placed in orbit around Bennu at a distance of 5 km. Bennu has an estimated mass of 7.0^.10¹⁰ kg. This all took place at about the same distance from the sun as the earth is. What would you predict about the force on the satellite from radiation pressure compared to the gravitational force from Bennu as it tried to orbit this tiny 'planet'. This is/was a real engineering problem for the mission control folks.

Assignment: HW: Light

Turn in the various (3) homework problems in this breadcrumb.

Assignment: Reading

Go on to the Polarization breadcrumbs where we will look at a variety of more complex applications of these principles