More than One Wave:

No doubt it is a little enthusiastic to assert that a simple wave travelling through a medium is something we have a solid understanding of. We haven't talked about absorption, polarization, refraction, and other effects that apply to every individual wave. On the other hand, isolated waves traveling through an endless medium are not the most common setting in which we observe waves. In true physics fashion we will first consider 2 waves (such a leap!) and in particular 2 waves travelling in opposite directions but otherwise sharing the same wave speed, frequency, and amplitude. While this might seem unnecessarily limiting it turns out, like neglecting air drag in PH211, we can develop a lot of insight into important settings without complicating the math so much. We will also explore, in future classes, two waves traveling in the same direction but different distances (interference), two waves traveling in the same direction with different frequencies (beat frequencies), along with polarization, reflection, and refraction. Buckle up and let's dive into the pool.......

Superposition:

Before we worry about any details of a particular setting we need to understand what happens if more than one wave is passing through a medium at the same time. Consider that what is actually happening (except for light) is that the wave is a result of forces pushing and pulling on the medium to make it move. If there are multiple waves then we 'merely' have to add up the collective forces from each wave and figure out what happens. Of course that is a bit of a wicked DE. The ultimate result however is pretty straight forward. At every point of the medium the 'height' of each wave at that point adds to the height of the other waves. This effect is called superposition and works (for the mathematicians) only because the underlying differential equation is linear. IF the DE is NOT linear then all bets are off and it's a computational physics problem.

[insert wick cool python notebook simulation here before I die]

Here's a lovely example of what multiple waves traveling through the same medium sounds like. John Bullitt is an artist in a unique way and this is a fascinating example of his work. Might make you think differently about the world. Sadly John has recently moved much of his work out of the public interwebs which is a loss but is understandable.

Two Waves (Opposite Directions, same A,f,and λ):

Consider the following mental or physical experiment. You are at the Oregon coast on a headland overlooking the waves rolling past on their way to the beach. Long slow rollers. What happens if you throw a rock out into the ocean? Two waves simultaneously? What does it look like? How might you express that mathematically? Does it match with the previous discussion about superposition?

Now consider this clip from a longer video from Roger Moore (not the James Bond actor apparently) at the University of Alberta. This is a demo many of us do laying a long spring on the floor of the hallway and sending pulses at each other along the spring. This video nicely illustrates that the real demo is much messier than the simulation that we physics types use to explain what we wanted you to see.

...and here is the sleek simulation of the same situation....

All of which is meant to give you some confidence that what we are saying about the linear superposition of waves is reasonable.

Here is a similar situation with actual waves in the ocean. The amplitudes are small so you have to watch closely to see the addition of the wave crests as they pass through each other.

 

Here's a little bit more dramatic clip with lower video quality....

 

Hopefully all this video abuse gives you some confidence in the veracity of the concept of superposition.

Two Waves (Opposite Directions, same A,f,and λ):

As you will have noticed in the last video one of the easiest ways to get two waves with the same A, f, and λ traveling through the medium is to reflect a wave from some boundary. Initially we will consider reflections off of rigid things like wall but we will dig a little deeper into the details of reflection in a moment.

Consider the first three of these animations (thanks Penn State!) which start with two pulses passing through each other and then move on to two waves travelling in opposite directions. You can see the application of the idea of superposition. These animations can't be paused which is unfortunate but I think you can see the superposition happening.

Mathematically we write down the description of a down the equation of a traveling wave (transverse) moving in the + direction and one moving in the - direction. Each has the same amplitude, frequency, and wavelength. The first is travelling to the right and the second is travelling to the left.

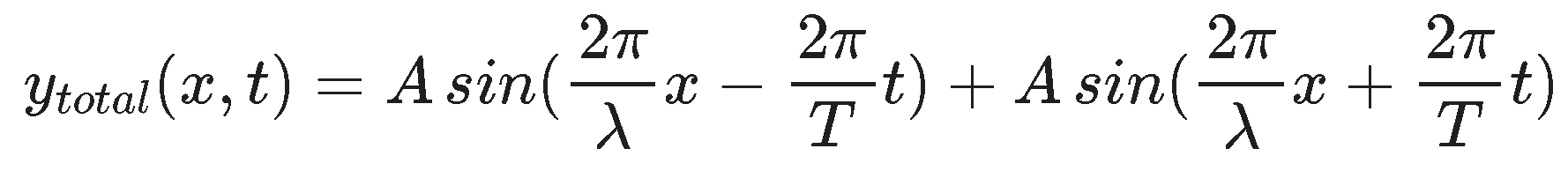
We can rewrite this expression in a mathematically suggestive way as...

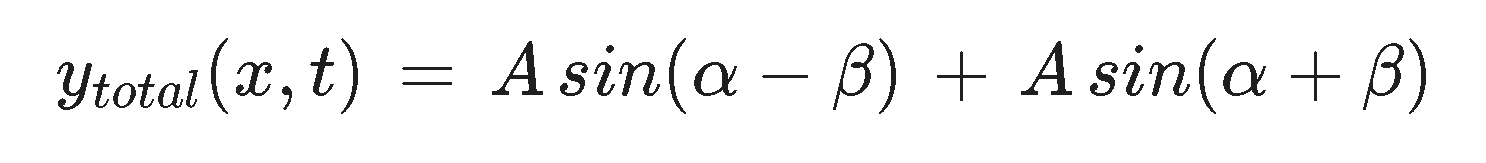
This suggests that one of those trig identities that your teacher told you would be useful one day is gonna be needed. If you chase through the trig and the algebra you arrive at this final form:

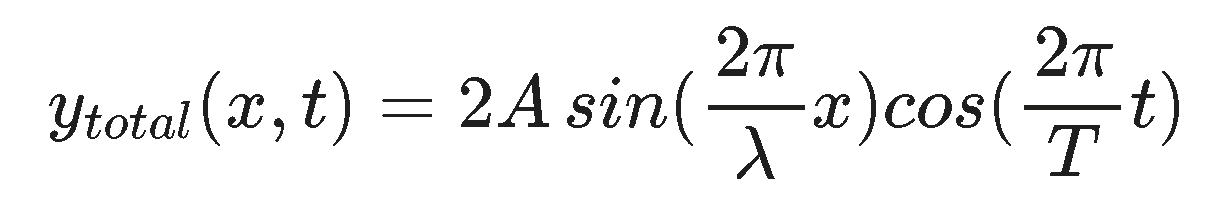
How does this connect with what you saw in the animations?

So now we have the idea that two waves of the same frequency and wavelength (only one is needed since the speed of the wave must be the same and forces the wavelengths to be the same if the frequency is the same and vica versa! - do you understand this?) traveling in opposite directions create a wave pattern that has the shape of a wave but doesn't go anywhere hence the name 'standing wave'. You can see this by noting that a value of x for which sin(kx) = 0 will always be zero regardless of the time and that means y(x,t) will always be zero. Can you find these points in the animation? Similarly, at some values of t the cos(ωt) = 0 which means y(x,t) = 0 everywhere along the x direction (it looks flat). Can you see this in the animation?

The physical points where y(x,t) is always 0 are called the nodes (they don't move). Pretty much makes sense that the opposite of a node is the place where the maximum motion happens. That point is called the anti-node. What is the relationship between the distance between the nodes and the wavelength of the waves which create the standing wave? Look at the animations and it should become clear!

You should be able to relate the wavelength of the underlying waves to the distance between nodes, and know what nodes are, and the amplitude of the underlying waves to the maximum amplitude of the anitnodes. The connection to periodic motion should also be clear along with all of the features of periodic motion we explored a couple of weeks ago.

Node to Node Distance (x_{node to node}):

x_{node to node}= λ/2

Don't forget this!!!!

 

The easiest way to get nearly identical waves traveling in opposite directions is to reflect a wave back on itself. Can you think of settings where a traveling wave in a medium is reflected? Why does it reflect?

Reflections (complications):

Here is another set of animations from the good folks at Penn State (thanks!) which start with standing waves again (although now showing how they establish themselves as the waves first meet -- nice stuff!). Following the standing wave animations are a series of animations illustrating the differences between 'hard' and 'soft' boundaries. A 'hard' boundary is where the medium carrying the wave is unable to move at the point of reflection and a 'soft' boundary is the opposite. Please notice that both types of reflections lead to standing waves though the specific behavior at the point of reflection is different. Notice that the rest of the characteristics of the standing waves are the same except for this boundary condition.

Here is a physical demonstration of the same reflections using a more formal version of the jelly babies wave machine. In this video clip the instructor refers to the 'hard' reflection as a 'fixed end' and the 'soft' reflection as an 'open end'. Just different descriptors for the same features.

 

More General Reflection:

In the previous cases we have looked at circumstances where there is no apparent wave that travels past the end fo the wave machine. All of the incoming wave is reflected. In general it's a little more complicated. Any time the medium carrying the wave changes there are both reflected and transmitted waves. Due to energy conservation the energy of the incoming wave will be divided between the reflected and transmitted waves (how much goes where is very complex- save it for your senior year). The transmitted wave always continues on with the pulse in the same orientation as the incoming wave. The reflected wave is sometimes flipped and sometimes not. Consider the following videos of pulses travelling down a chain with different densities. Notice the transmitted wave crest moves smoothly through the transition and only changes amplitude. In the first case (from the previous jelly baby video) the incoming pulse (up) is reflected as an up pulse (same orientation). In the second case the incoming pulse (left) is reflected as an inverted pulse (right) in the opposite orientation.

 

Rule for Reflection:

IF the transmitted wave speeds up in the new medium the reflected pulse (wave) is NOT inverted. If the transmitted wave slows down in the new medium the reflected pulse (wave) IS inverted.

This will be important in a few weeks when we look at thin films and optical coatings.

Take Aways:

There are two take aways here. The first is that changes in medium lead to both a reflected and transmitted wave which is how we commonly end up with two waves traveling in opposite directions. Secondly, 'fixed' ('hard') ends of media don't move (nodes) while 'open' ('soft') ends are free to move (anti-node) as the wave reflects.

Concrete Example:

Standing waves on a string. This demo is one I usually do in class which is always a bit more fun. Here it is as a video clip (thanks James Dann!).

Separate from James' comments lets look at this through the lens we have developed here. The wave generator (speaker driver) shakes one end of the string at a particular frequency which propagates a wave down to the other end where it reflects. Do we have the basic conditions for a standing wave? -- do I have to answer that?

Boundary conditions:

To help connect this to our math classes we should note that this string has boundaries (ends) where certain conditions must be met. At the far end from the driver is the boundary condition a 'hard' (fixed) or 'soft' (open) end? Hopefully you observe that the string is tied to the post which is the definition of a fixed end. Thinking back that means that there must be a node at this point. Looking at the wave driver it appears that this boundary is also a node. This may be a little puzzling but it is an example of driven periodic behavior where the wave driver only moves a tiny amount (a node) but because it's a the 'right' frequency it keeps adding energy to the wave.

Conceptually:

We have a string of some length L that has two waves going in opposite directions with the same frequency and wavelength. From our earlier discussion this must form standing waves with nodes and antinodes. In addition the boundary conditions require that there are nodes at both ends of the string. How do we get both of these statements to be satisfied?

Paper and Pencil!!!!!

This is another one of those times (like always) where drawing a picture is absolutely essential to working out a solution at least in the begining. Here's how the process works.

Once you see all the patterns we can determine the wavelengths for each possible standing wave pattern. If we can determine the frequency then we can calculate the wave speed or vica versa. The baseline assumption is that the speed of the wave is independent of frequency which, like many things in physics, is not quite true but is a very good approximation. We'll wait until next time to sort out the mathematical pattern for these standing waves.

The image below shows similar patterns to the ones we just found along with the naming conventions for those patterns. Note the subtle and irksome distinction between overtones and harmonics. The simplest possible pattern in a given setting is called the fundmental or 1st overtone and successive patterns are labelled as shown.

 

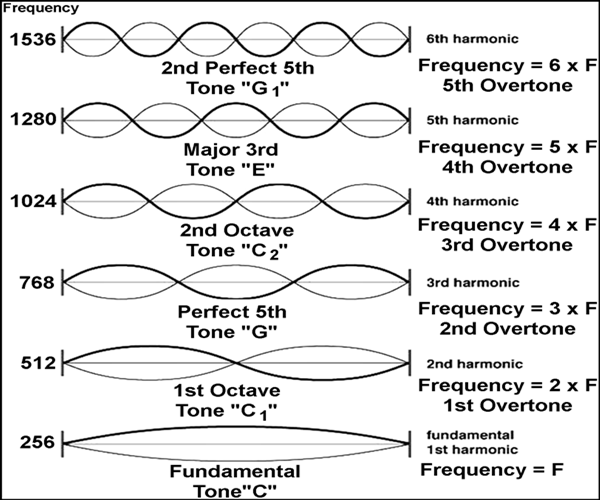
The primary tools for all these HW problems are sketching combined with v = λf!

HW: Standing Waves

Blowing across the top of a soda bottle produces a loud low pitched sound. Explain why the pitch of this sound is higher when the bottle is partially filled with water. (there are physics reasons that have to do with the standing wave patterns -- if you want to get more precise you can refer to discussions of Helmholtz resonators)

HW: Standing Waves

The lowest note on the piano is 27.5 Hz and is produced by a string that is 1.18 m long (for an upright piano). An important thing to know is that the tension in all the strings in a piano needs to be the same to keep the frame from warping. This means that the speed of the wave on the string is the same regardless of the length (remember the integration problem with the rope?). If, for efficiency of manufacturing, the same wire is used to produce the highest pitch on the piano (5096 Hz) how long would this string be? Does this seem like a sensible way to build a piano? Find a piano and peer into it -- how do they solve this problem and what is the physics behind it?

HW: Standing Waves

The lowest string of the guitar is intended to have a fundamental frequency of approximately 161 Hz. The highest string on the guitar has a fundamental frequency of 645 Hz. In order to avoid nonuniform strains in the neck of the guitar all strings should be under the same tension and they are also the same length (except for the odd one on a banjo!). What is the ratio of the mass of the lowest string to that of the highest string? This is closely related to the previous question (this uses information from our previous rope integration problem -- remember the linear mass density?).

Assignment: HW: Standing Waves

Turn in the various (3) homework problems in this breadcrumb.

Assignment: Reading

Go on to Standing Waves II to move to our discussion to applications of standing waves in a variety of contexts.