Standing Wave Applications:

There are many settings where standing waves come in to play. We will consider a subset of those which are mostly 1D. Everything that we do can be extended to 2D and 3D though the math gets much more exciting.

Pulses, Frequency, and Damping:

An important feature of all applications of standing waves is the how the wave gets started travelling back and forth in/on the medium and what happens to waves whose frequencies don't match natural frequencies of the system. Sometimes, like the wave driver in the example from the last breadcrumb, we are sending waves of a very specific wavelength and frequency out into the medium to be reflected. Other time we are 'plucking' a string which makes a single pulse. Remember that a pulse is made up of (Fourier analysis) of many waves of different frequencies that combine to create the pulse. Any wave which has a frequency that doesn't create a standing wave that matches the boundary conditions will be 'fighting' it's environment and lose energy quickly. When we keep shaking the string at a 'bad' frequency the system fights with the driver and can't establish a consistent pattern. In the case of a pulse the string or wave medium acts as a filter and rapidly eliminates parts of the pulse that don't match the natural frequencies of the setting and allows frequencies that do match to continue to propagate.

Stringed Instruments:

Consider a violin or guitar string. There is a string of some kind placed under tension and it crosses some object at both ends that prevents the string from moving. We pluck it or bow it to produce pulses which are made of many sine waves of different frequencies (thank you Dr. Fourier!). Those waves will reflect from both ends with limited loss of energy creating the conditions for a standing wave. Only those frequencies that match the boundary conditions will be able to persist.

Here are the steps we take to work out what to expect.

i: We sketch the heck out of the system for starters. Be sure to indicate your understanding of the physical setting at the ends of the system.

ii: Decide whether the end points of the medium are nodes or antinodes (are they free to move or not?)

iii: Are there other constraints on the medium that we need to add to our sketch? For sound waves be careful to distinguish between displacement constraints and pressure constraints.

iv: Find, by sketching, the simplest pattern that fits boundary conditions or other constraints. If needed consider other potential self consistent patterns.

v: Determine wavelength of pattern(s) and their frequencies assuming wave speed is known.

vi: What was the question? Now, perhaps, you're ready to answer any questions that were asked about the system.

Applying these steps to a guitar or violin string we see that:

i: the string is constained (fixed) at both ends ....

ii: ....which means the ends must be nodes.

iii: There are no other constraints on the system. This is NOT a sound wave so none of those worries.

iv: Here is the sketch of the possible standing wave patterns from previously.

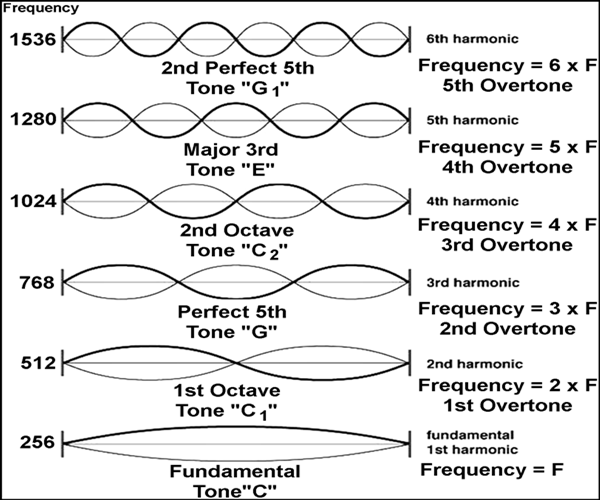
v: Now we need to determine the wavelengths and frequencies. Remember that the node to node distance is λ/2. This means that for the fundamenal λ/2 = L (the length of the string). We can continue through the rest of the possible patterns as shown in the video. Also remembering that v_wave = λ f we can also determine the frequencies using f = v_wave/λ. (my apologies for the sudden volume change -- not sure what happened)

vi: What was the question? Never mind.....The key result of this analysis is this expression for the possible wavelengths of the standing waves...

and this expression for the possible frequencies of the standing waves....

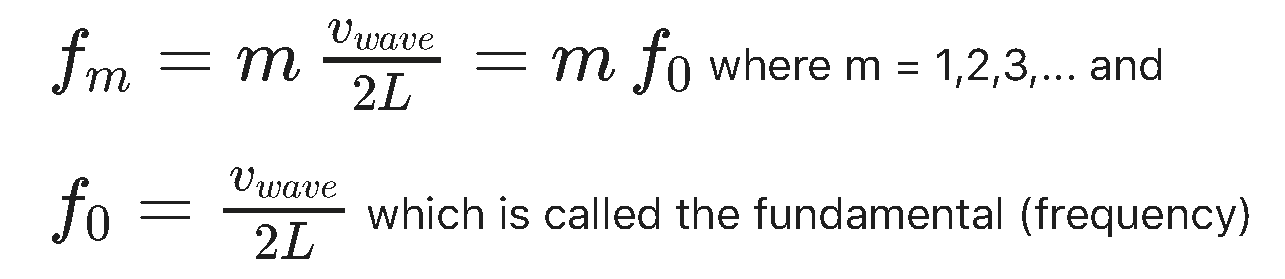
Notice that what these two expressions tell us is that the possible standing wave frequencies on a string of this kind are every multiple of the fundamental frequency. Does that match what is in the earlier image? Notice that all of the frequencies are multiples of 256 Hz.

In these expressions m is NOT mass. In many texts you will see n used as the counter instead of m but we are going to need 'n' to mean something else in little while so I hope to avoid confusion by using m instead.

NOTE: m is just a counter!! IT DOESN'T MEAN ANYTHING IN PARTICULAR!!

Side Note: For the musicians in the crowd:

You might want to notice that the first 7 harmonics on a string all form a C major cord assuming the fundamental is a C. When you pluck a string all of these frequencies are successfully reinforced by the string. This makes the sound of the string much more attractive then just playing a 256 Hz sine wave. You can replicate this effect by opening 3 or more windows with this web tone generator and playing the first 3 harmonics simultaneously. You will find that even if there is a little bit of the 2nd and 3rd harmonic playing it sounds much nicer that just a single frequency sine wave.

It is also interesting to note that, in general, when a string is plucked the dominant standing wave is the fundamental and the successive harmonics have smaller and smaller amplitudes and are therefore quieter.

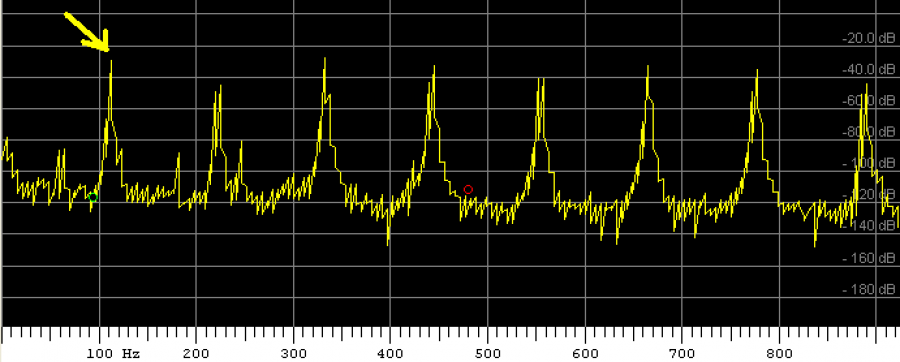
Thanks to this anonymous experimenter for the spectrum

You may notice that it doesn't seem like the loudness of the harmonics are decreasing much. Notice that the vertical scale in this plot is a log scale where -20 dB is a factor of 10 in amplitude.

Tuning:

A last discussion before we leave strings. Think back to the homework problem with the pulse travelling up the hanging rope. What was the connection between the wave speed and the tension in the rope/string?

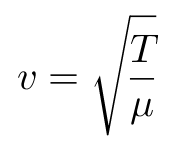
So what happens to the wave speed if I increase the tension in the string? If the wave speed increases what happens to the fundamental frequency? So, by increasing the tension in the string we increase the wave speed which causes the fundmental frequency to increase which is called raising the pitch. This is the physics behind tuning a stringed instrument.

Activity: Now assume that you are touching your finger or some other object 1/3 of the way from one end of the string (don't push hard just touch). This forces the standing wave to have a node at this point but the waves still travel all the way to the end. What are the possible standing wave patterns?

Example of Harmonics in Action:

Brian D noted that there is this fabulous example of harmonics in action. This video is of Victor Wooten playing a cover of Amazing Grace on a bass guitar using a mix of 'normal' bass notes and harmonics created by the process you discussed above.

Video of Violin String:

Sound Waves in a Tube:

The next application of standing waves is to sound waves travelling back and forth in a tube. There are several examples of this to be considered. Pipe organs represent an application of sound waves travelling back and forth in tubes of different lengths.

Thanks to wikimedia for the image

The engineering talents of Blue Man Group are also an application of sound waves in a tube.

 

Boundary Conditions for Sound:

The boundary conditions for sound represent a special case that is worth addressing directly. There are actually two things happening in a sound wave. The air is displacing back and forth laterally (since it is a longitudinal wave) AND because of the displacement the pressure at different points in the medium is increasing and decreasing periodically as well. Consider the following illustration from the hyperphysics project.

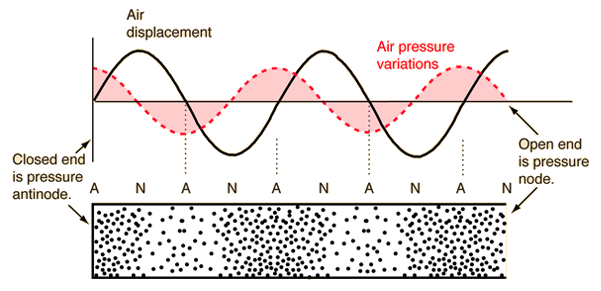
This takes a little mental gymnastics to make sense of this but if you think about the point in the standing wave where the air is NOT moving (displacement node) then on either side of that point the air is moving towards the node squeezing it to a high pressure or it is moving away on both sides lowering the pressure. This is the definition of a pressure antinode. The take home message is that the pressure nodes and antinodes are precisely flipped from the displacement nodes and antinodes.

Boundary Conditions and Constraints:

IF the physical system keeps the air from moving then that location (the closed end of the tube above) must be a displacement node since the molecules of air can NOT move. The open end of the tube is a displacement antinode because the air is free to move. From a pressure perspective the pressure at the open end must match the air pressure surrounding the tube so it must be a pressure node and conversely the closed end allows the air to be squeezed against the closed end making a pressure antinode.

Returning to the problem of the open tubes illustrated earlier.

i: The tubes are open at each end.....

ii: .. which means there are displacement antinodes at each end. No other constraints on the system yet.

iii: No other constraints on the system yet.

iv: Sketch the possible standing wave patterns..

v: Now we need to determine the wavelengths and frequencies as we did before.

vi: What was the question? Never mind.....The key result of this analysis is this expression for the possible wavelengths of the standing waves in an open tube is that they are the same as the string clamped at both ends! I won't repeat those results here.

What is the Commonality?

Since the results of these two seemingly different setting are the same there must be some commonality that we can articulate. There are a number of ways of stating it but generally we describe the feature both cases share as having 'symmetric' boundary conditions. Be careful! The results are only the same if there are no other constraints on the system. Simple strings clamped at both ends and simple tubes open at both ends behave identically. Any other constraints and you need to stop and reassess.

Activity: Now assume that you put a hole in the tube (open at both ends) exactly in the middle of the tube. What does this do to the standing wave pattern? Does the hole force a pressure or displacement node/antinode at that location? What are the possible standing wave patterns?

HW: Standing Waves Applications

The resonator tube under the lowest note of a marimba (a common performance instrument at Bend festivals) is 85 cm long and open at the bottom end. What does the physics of standing waves say about the lowest resonant frequency of this tube?

HW: Standing Waves Applications

Your barbershop quartet is on a trip together and find yourselves at the entrance of a tunnel where you can't see the other end. Knowing that tunnels give great resonances you try singing into the tunnel. After much experimentation you find that an inverted D7 chord really makes the tunnel sing (resonate!). The frequencies in this chord are 110 Hz, 130 Hz, and 145 Hz. These must be standing wave frequencies of the tunnel but they are not necessarily all the frequencies or even successive frequencies. What is the shortest possible length of the tunnel consistent with this data? ( Hint: look at the ratios of the frequencies)

HW: Standing Waves Applications

This is an actual experience you might have if you are ever moving irrigation hand lines in Central Oregon. You carrying a 12 m length of irrigation pipe (40 ft) which you are holding in the middle. The point where you are holding it must be a node. What are the wavelengths of the first 4 possible standing wave patterns? Be sure to follow our process with sketches etc. The frequency of the fundamental is 1.2 Hz (from personal experience). What is the speed of the wave travelling along the irrigation pipe?

 

Assignment: HW: Standing Waves Applications

Turn in the various (3) homework problems in this breadcrumb.

Assignment: Reading

Go on to Standing Waves III to move to our discussion to further applications of standing waves.