Waves:
What is a wave? What are the characteristics of the things that we call waves?
Physical Waves: water waves of many types, seismic waves, others we can see?
Invisible Waves: Sound, light, other's we can't 'see'?
Not Waves: wave functions (quantum), hand waves (why not?), sine and cosine funcs, others?
What is the difference between a wave and a pulse? What do Fourier series have to do with this? Remember that we can represent any time dependent shape (including a pulse) by some potentially complicated combination of harmonic functions. This includes describing a pulse (localized) with sine functions (infinite range) in some complex combination.
Ocean Waves:
Working from this video do you see the two different kinds of periodic behavior? Temporal and spatial? What would plots of these two different periodic behaviors look like and how do the features of the plots connect with what you see in the video?
The important features of the reality and the plots are Amplitude, period or frequency, wavelength, and wave speed. Identify each in the video.
Activity: Which features of the two plots below will have to change to describe the ocean waves in the video (using Bruce math of course!). The plots show general features of a wave which you can now adapt to the specifics of the setting.
Spatial Periodic Plot: (what the wave looks like at a specific moment in time - snapshot!)
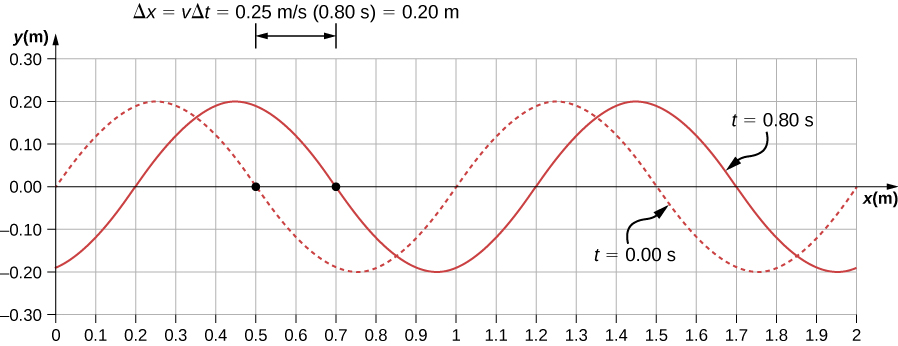
Thanks to UBC University Physics OER text for the use of these images
Temporal Periodic Plot: (what the behavior of a particular point of the medium (water) looks like - Fixed Point!)

Thanks to UBC University Physics OER text for the use of these images
What is the relationship between the features of the plot and the speed of the wave?
v = λ * f = λ / T --- DON'T FORGET THIS!
Mathematically we should be able to combine all of this behavior into a single expression.
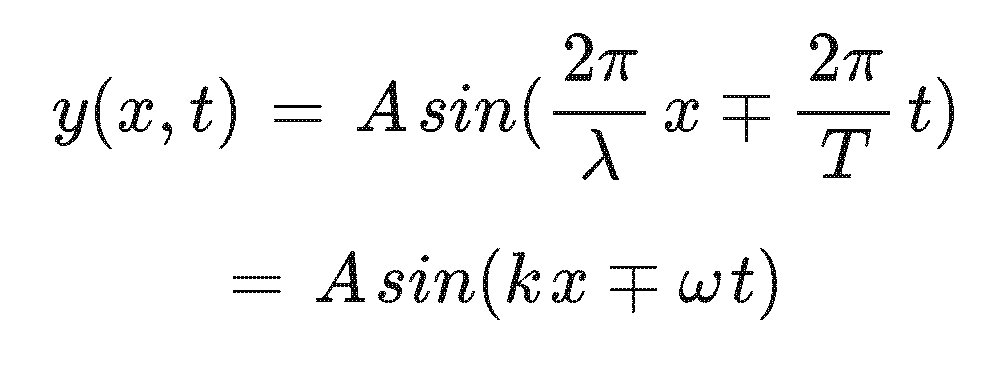
In this expression k is called the wave number and has units of m-1 and ω is the angular frequency or velocity and has units of s-1. I write it this way to make it clear where the wavelength and the period contribute. The - and + are required to distinguish between a wave traveling in the + x or -x direction. Which one is which do you imagine?
If I pick a specific value for x then the first term in the argument of the sine becomes a contant and we have a function that is periodic in time just like we have been looking at. I personally refer to this as the fixed point representation. It describes the motion of the duck (or the beaver) sitting on the wave as it goes up and down.

If I look at the whole ocean at a particular moment in time (like I froze the scene) then the second term inside the argument of the sine becomes a constant. Now I have a spatially periodic function that describes the shape of the waves across the ocean as a function of x.

The Medium:
Would these waves exist without the water? We call the water the wave medium. What are the media for the other waves we discussed earlier? You should be able to identify the physical medium for the wave in every case other than light. Light is a special case that we will talk about later.
What do you think will happen (and why) if the characteristics of the medium were changed? What if we substituted mercury for the ocean? For the same energy you don't need to lift mercury as high so the amplitude would probably shrink. Because mercury is more dense it would be harder to accelerate vertically so probably the wave would slow down and well. The core idea here is that it is the physical characteristics of the medium that determine the speed of the wave.
Goofy version of human wave
So here is a more controlled and physics version of a wave... this is pretty nice. Formal equipment like this costs several thousand dollars:)
In the previous video the teacher illustrates many of the features of waves that we have discussed along with a couple more.
Slinky waves...to start to grok the distinctions between transverse and longitudinal waves read this web page (ignore the stuff about standing waves -- that's next week) and then watch the following videos.
Transverse Waves
Longitudinal Waves
Sound waves are longitudinal waves and water waves are transverse waves. Seismic waves come in three varieties, P (pressure) waves which are longitudinal, S (shear) waves which are transverse, and L waves which are also transverse.
HW: Basic Waves
It is sometimes said that person “can not hear sound whose wavelength is larger that the size of your ear”. Test the veracity of this statement given that the speed of sound in air is 343 m/s and the human ear can usually hear sounds from 20 Hz to 20,000 Hz. (As we get older we tend to lose sensitivity on the high frequency end as you will notice during a future class)
HW: Basic Waves
The wavelength of a sound wave in air is 2.74 m. As the sound
runs into the surface of a pond the wave is transmitted into the water. What
is the wavelength of the sound in the water? Assume the speed of sound in
air to be 343 m/s and that of sound in water to be 1480 m/s. There is one additional concept you will need to be clear about to solve this problem (and I'm not saying what it is!).
v = λ * f = λ / T --- DON'T FORGET THIS!
Activity: Do the following calculations for various sound waves. The math is simple so get it done and spend some time noticing whether there are interesting patterns as a result.
Now --- the speed of sound turns out to be 343 m/s at sea level in air. I don't really care about the precision here so I'd be happy if you remembered 300 m/s but 343 m/s is such a symmetric number that I just like it. The frequency of human speaking sounds is around 200 Hz. Smaller (lower) frequencies for men typically and perhaps a little larger (higher) for women. What is the wavelength of a 200 Hz sound wave by calculation? What about elephant sounds at 20Hz or dog whistles at 20 kHz? Surprised?
Look up the speeds of seismic waves (P and S waves are different). Knowing that the frequency for seismic waves is between 0.1 and 10 Hz calculate the wavelength of a typical seismic wave. You should get really long wavelengths!
HW: Basic Waves
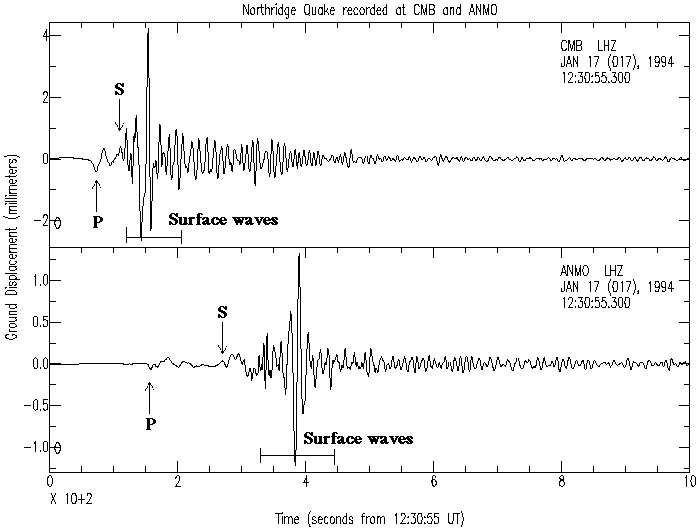
Here's a real life (and challenging) question. The seismic data below was recorded at Columbia, CA and Albuquerque, NM respectively. As you can see from the data the arrival times for the P and S waves are different for each location. Based on this data and the assumption that the P and S waves have the consistent velocities what is the speed of each wave?
There are many things I am 'testing' with this problem. It is a variation of the thunder and lightning calculation. For some discussion of this stuff take a look at this website. Here's another source that includes a range of wave speeds. What wave speed should you use (remember whose class you are in!)? Why do you need to know where the data was recorded? Can you understand the plots? Does your data confirm the location of the earthquake in Northridge CA?.
Tsunami:
A tsunami is another sort of wave. Based on satellite data NOAA created this animation of the Indonesian quake of a few years ago. By observing the animation and refering to maps of the world you should be able to estimate both the wave speed and the wavelength of the tsunami. Notice how freaking fast it is going! Then calculate the period between wave crest arrivals. We will talk about this a little from a safety perspective next time in class.
Wave Nature of Light:
Here's a great presentation by Veritasium of the 'proof' that light must be a wave (at least in part!)..
Things to think about:
The speed of light is quite fast as you may be aware. The standard symbol for the speed of light is c. If you see a disembodied c in a physics it probably represents the speed of light. With very high precision c = 3.0.108 m/s. How many times around the earth at the equator will light go in 1 sec? How long does it take light to get to earth from the sun?
We usually think of the colors of light in terms of wavelength. Here are some good numbers to remember λ red = 650 nm, λ green = 550 nm, λ blue = 450 nm. What are the frequencies associated with these wavelengths? Radio waves are also 'light' with a frequency in the MHz range for FM radio. OPB is at 91 MHz, what is the wavelength of this wave?
HW: Basic Waves (integration)
Consider a pulse, a wavelet, traveling up a hanging rope. As you have noticed in our class explorations the speed of the wave depends on the characteristics of the medium carrying the wave. What characteristics of the rope could affect the speed of the wave as it travels along. Confirm your understanding in this one page pdf on the speed of waves in ropes. [Thanks to the Caltech Physic League for this short paper!] You will need to read carefully since the paper uses slightly different language at points. The last expression is the one you need to understand.
Given the critical engineering information you have gleaned from your observation of ropes and the paper we now can apply it to a hanging rope. Which of the factors affecting the wave speed change at different points on a uniform hanging rope? Now you have all the pieces you need. Calculate the time it takes for a pulse to travel up a hanging rope of mass 2.5 kg and length 9.5 m. This is a calculus problem that involves freebody diagrams to start and clear setup to get the integral. Remember that if the speed of the object is changing you can add up how long it takes to travel little distances (can you say 'dy'?) assuming the speed is constant for that short distance. Doing the integral is pretty easy it's setting it up that's the challenge! You'll know you have it when you get 1.95 s for the answer.
Thunder and Lightning:
Before you start this section be sure you write down on a piece of paper what you were taught or know about determining how far away lightning is. People usually do this by seeing the flash and counting seconds and converting those seconds to a distance. What was the rule that you learned? My daughter remembers learning it from a children's book called 'Thunder Cake'. Don't cheat -- write it down!!
Now -- figure it out. Assume you're 1 mi or 1 km from a flash of lightning. How long does it take the light to travel from the lighting to you? You should expect to get a very short time (in the μs range). When the lightning passes through the air it heats the air rapidly which produces a pressure wave (sound) -- transverse or longitudinal wave? -- that also takes some time to get to us. How long does it take the sound to travel 1 mi or 1 km? (you should get a few seconds for these answers depending). What is the correct rule for estimating the distance to the lightning? IF you didn't get 4.7 s/mile or 3 s/km go back and check your work until you get it right:) How far away is lightning if you see the flash and then hear the boom in less than a second? Please remember this and teach your children well!!!
Assignment: HW: Basic Waves
Turn in the various (4) homework problems in this breadcrumb.
Assignment: Reading
Go on to Standing Waves I to move to our discussion of the superposition of waves and an important set of special cases.
