Fynman Diagrams: A New Representation

In the 60's particle physics was really starting to get off the ground and it seemed like every day there was some new confusing data or particle that we needed to make sense of. Over time people tried a number of ways to represent what seemed to be going on with varying degrees of success. One important idea that emerged during this time was the idea that when objects interacted they did so through the exchange of information. What exactly that information is/was is still fuzzy for me but I think of it as field 'information' whatever that is. The exchange of information had to be 'carried' by something which led to the idea of 'exchange particles'.

In this conceptual model each type of field had a particle that was formed by changes in the field that carried the information. Light is a result of changes in the EM field and it already had name for it's particle - the photon. For gravity we imagined a particle like a photon that was the result of gravity waves and we called it the graviton. The other two forces we know about in the universe, the weak and strong nuclear forces, must therefore have exchange particles as well. The primary difference is that there are multiple exchange particles for these nuclear forces.

Feynman diagrams are a tool for describing the way in which we imagine particle interact through the EM, weak, and strong forces. As far as I am aware gravitational interactions between particles are not described with Feynman diagrams.

Feynman Vertex (vertices):

A vertex in a Feynman diagram is a representation of a fundamental interaction that is possible. At each vertex various quantities must be conserved. With some limited exceptions a vertex is a 3 legged creature. Typically two represent particles and one is an exchange particle. Here is a general primitive vertex.

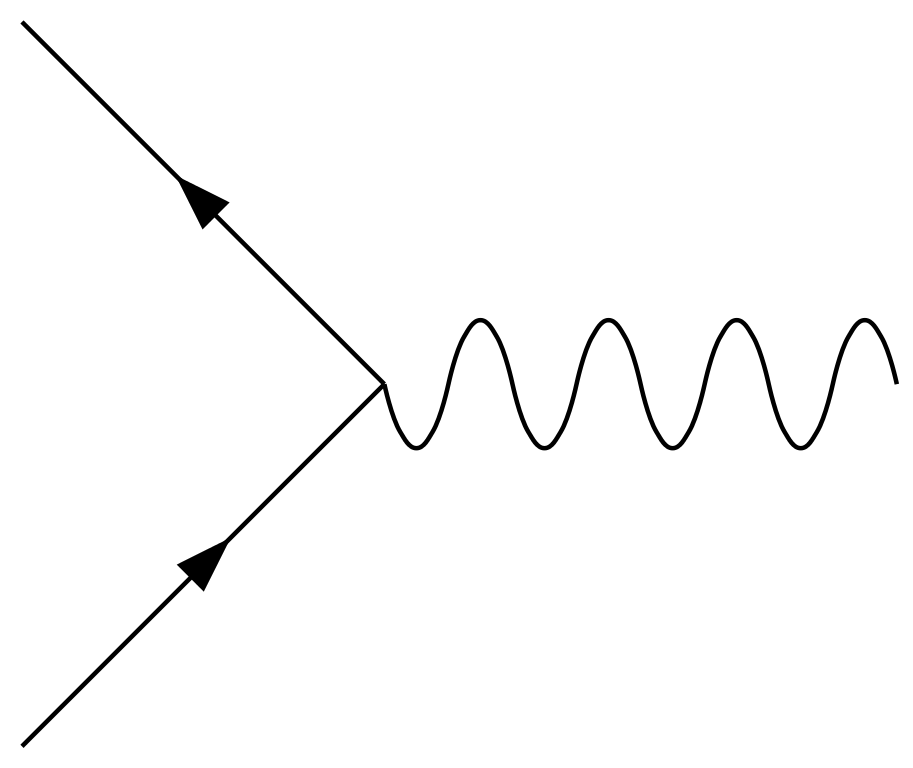
The two directions in this vertex (horizontal and vertical) represent space and time. It is aggravating that there is no solid convention for which is which. I learned it as time flows up and space is horizontal. Other reverse the axes. We will take the time is vertical model. Solid lines represent particles and a variety of wiggly lines represent the exchange particle. Here is a simple vertex representing an electron 'releasing' a photon.

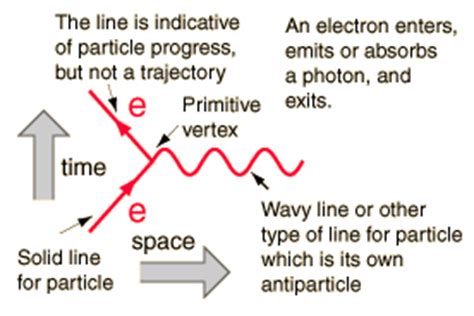
Examining this vertex allows us to consider how various physical quantities must be conserved. Momentum and charge must be conserved. The photon carries momentum that allows the initial rightward momentum of the electron to be conserved. An electron enters and exits from the vertex which assures that charge is conserved.

Orientation:

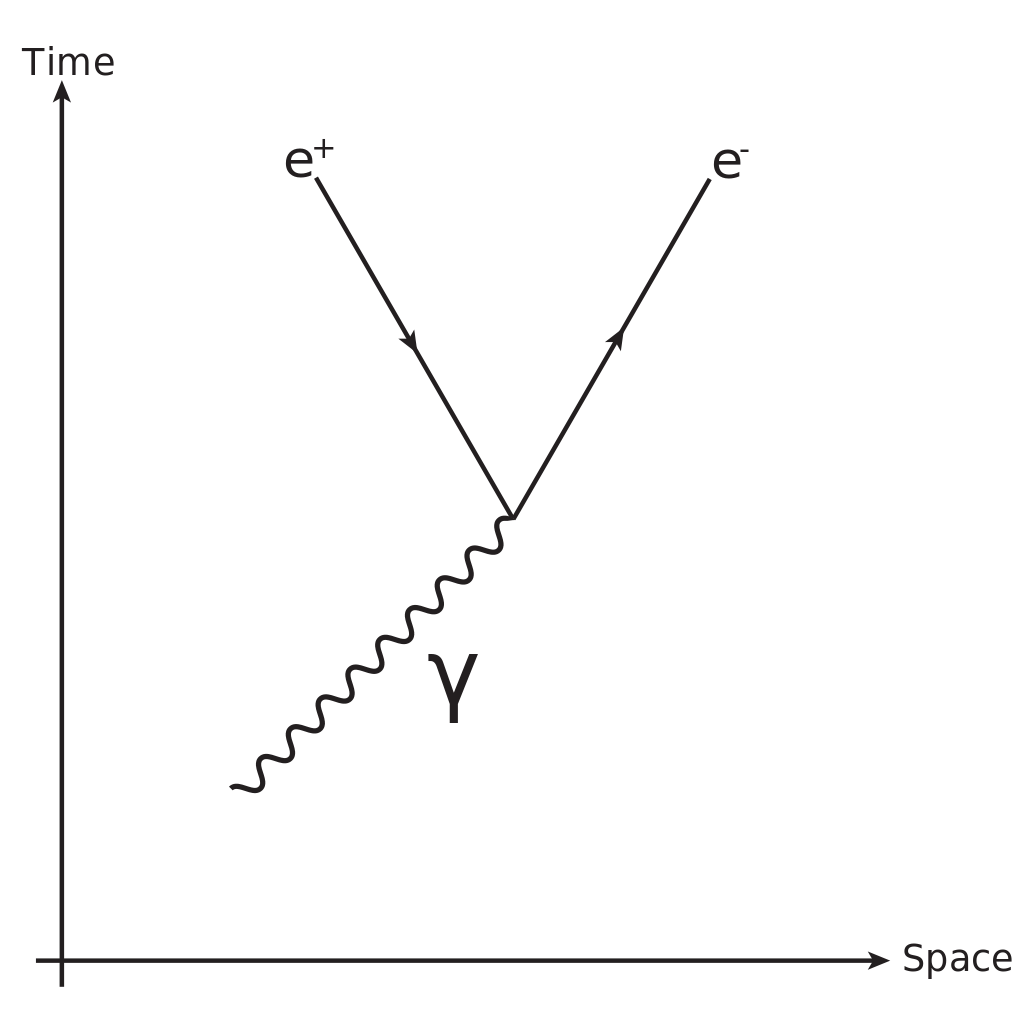
Primitive vertices can have any orientation as long all appropriate physical quantities are conserved. Here is the same vertex from above in a different orientation. The story this diagram tells is of a photon traveling along and 'decaying' or transforming into two particles. A simple reading of the diagram says, confusingly, that one of the particles is traveling 'backward' in time. The interpretation that Feynman applied is that particles traveling 'backward' in time are the antiparticle. So, in this case, the electron is the forward moving particle on the right and the positron (an electron with positive charge - an anti-electron) is the forward moving antiparticle on the left. Notice that charge is conserved - 0 before and neutral after. You might will wonder why, if this is possible, it doesn't happen all the time. Remember E = mc²? The photon has to have enough energy to create the mass of the electron and positron and also some extra energy to assure that momentum can be conserved.

This is why we often list the (rest) mass of particles in energy units. Here is the small table for electrons.

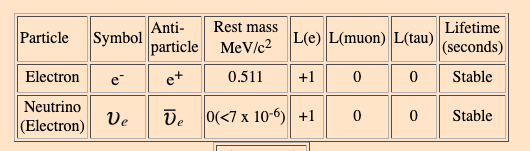
This means for a photon to create an electron-position pair it must have an energy somewhere over 1 MeV. Here is a graphic with the energy for a single photon indicated. You can see that is has to be a very energetic photon to even have a chance. Visible light has nowhere near enough energy.

More common Feynman diagrams involve two vertices like these...

Photon Pair Production:

The annihilation of an electron and a positron can't be satisfied with a single vertex due to momentum conservation requirements. As a result this process always produces two photons headed in opposite directions. This helps us appreciate that just because you can draw a particular Feynman diagram doesn't mean that what you are showing is possible. It still has to be checked against other conservation rules. See if you can recast this diagram into words and verify that it conserves charge, energy and momentum. The particle which connects the two vertices is called a virtual particle because it never shows up in the physical world.

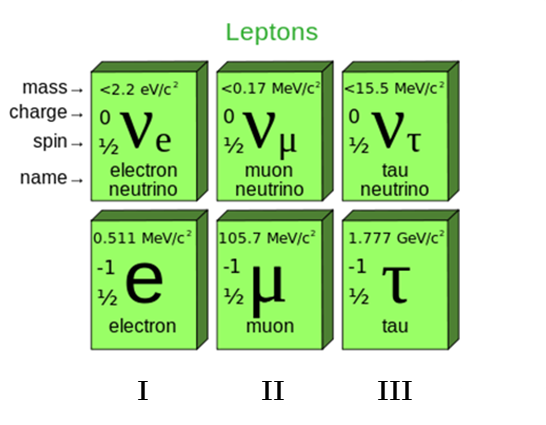
Leptons:

Now we need to add some new ideas and conservation laws. In the 60's as we started having the tools to explore particle physics by crashing things into each other it seemed like we kept having to update our thinking all the time. It's no wonder the collection of all the particles we were finding was referred to as a zoo. One subclass of those particle were identified as sharing properties in common with electrons. We observed that there were creatures in the zoo which seemed like heavy electrons and really heavy electrons. At the same time there was evidence for really light (m=0?) particles that were neutral and participated invisibly in interactions with electrons. This was challenging because neutral particles don't leave traces in particle detectors. Here is an example of an 'observation' of a neutral particle. Something like this led to the discovery of neutrinos. Just to the left of center near the top edge of the image is a short track that abruptly terminates with a single charged particle visible traveling up and to the right. To conserve momentum there must be a neutral particle going off in another direction.

Eventually we identified three types of leptons (called flavors or generations) which are shown in this table. The patterns of particle production observed indicate that (in general) the lepton number (the number of leptons of each flavor - I,II, and III) must be conserved as well. Radioactive β decay is a process which illustrates some of the factors that pushed our understanding of leptons.

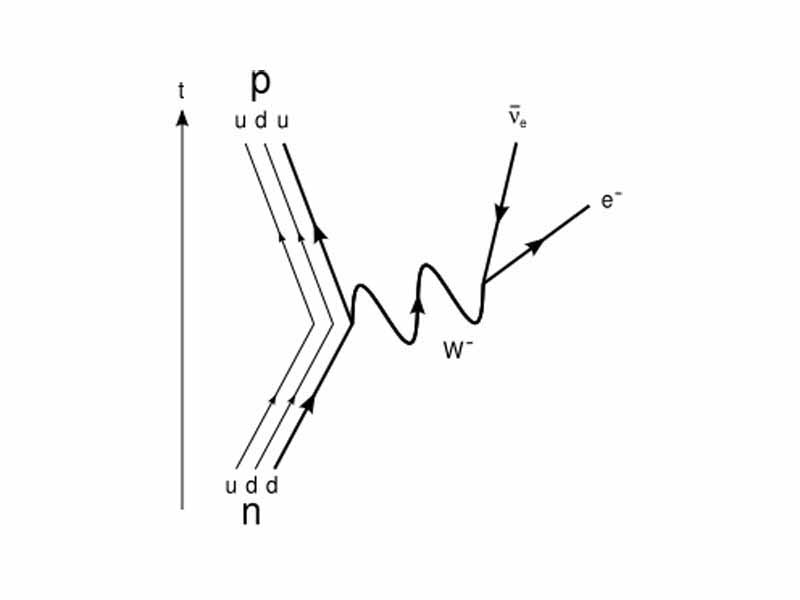
In radioactive β decay a nucleus 'converts' a neutron into a proton and emits an electron. On the surface this seems to NOT conserve the lepton number since after the decay we have one more electron than we had before. Charge is conserved but the lepton number is not. Here is the Feynman diagram for β decay.

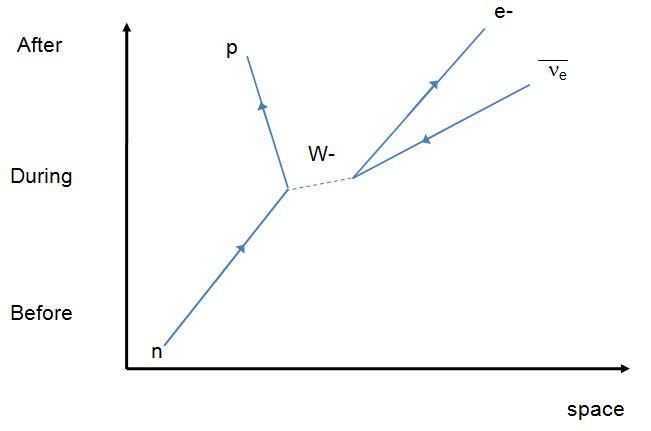
For this to work there must be an exchange particle that carries charge (unlike a photon). The dashed line is how we indicate the exchange particle for the weak interaction. In this case the exchange particle is a W^- called a W boson. The electron has a lepton number of +1. The 'electron anti-neutrino' has a lepton number of -1 (due to anti-particle-ness). Lepton number is conserved.

Quarks:

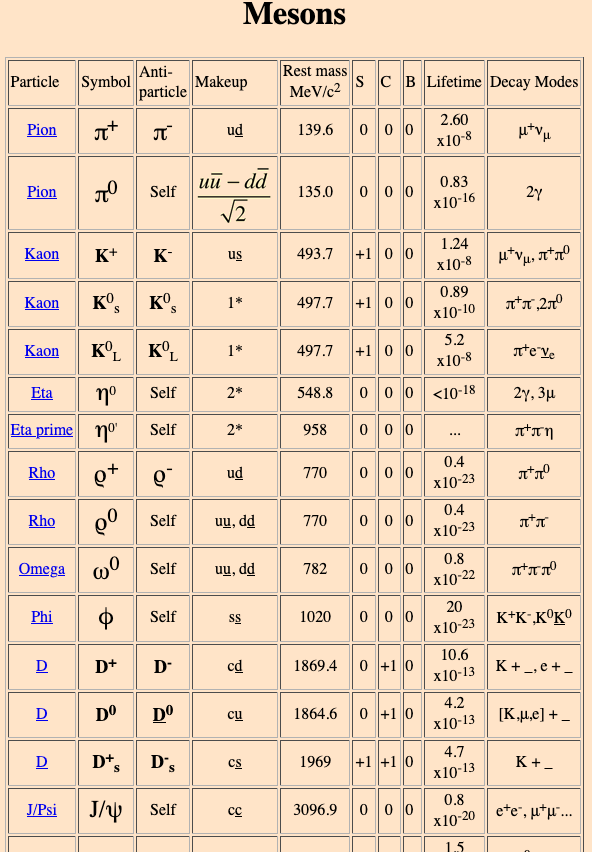
We are going to get lost here pretty soon because this stuff goes very deep and wide. Let's try to keep it simple by saying that in the many many particles that were observed there are some that are heavier than leptons but not as heavy as objects like protons and neutrons. These middle mass objects are called mesons, and the hefty proton like particles are called baryons. As we dug deeper an explanation came to the surface that identified the mesons as being built from two smaller particles and the baryons from 3 smaller particles. Collectively the mesons and baryons are called hadrons. These smaller particles are called quarks and have never been observed individually. There existence is inferred from a variety of experiments but not from direct observation. Like the 3 flavors or generations of leptons there are also three generations of quarks. Here is how it shakes out....

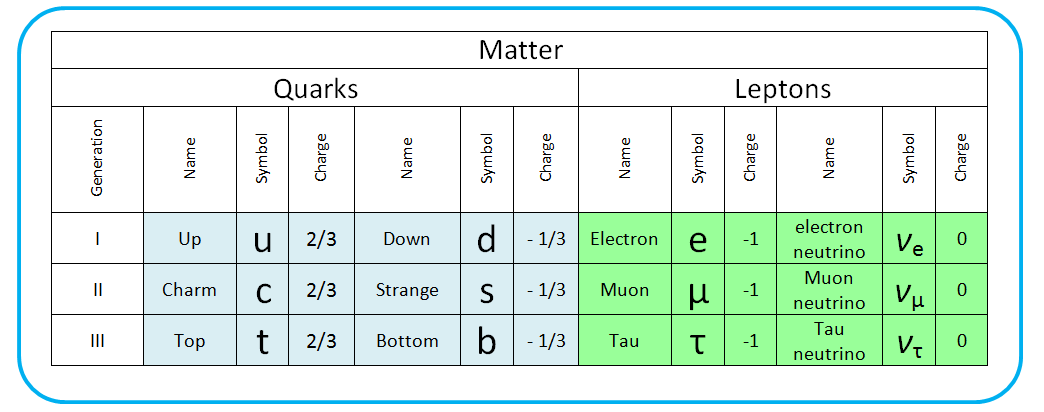
These tables show our understanding of how quarks go together to create mesons and baryons.

So now we can express our previous β decay process a little more explicitly.

Deeper and Deeper:

You have now seen an EM vertex and some of the interactions it describes and you've seen a charged weak interation (β decay). There are also neutral weak interaction vertices (Z bosons) and then the quark - quark interactions mediated by gluons of various kinds. If that isn't enough then there is also the color charge of each quark as well as it's charm, strangeness, top-ness, and bottom-ness which are conserved. I hope that this basic intro to the basics of Feynman Diagrams gives you a way to look at something like this and at least make a stab at understanding it. The loopy exchange particle is a gluon and the W boson is shown as a wavey line like a photon which is not consistent with the standard of dashed lines for weak interactions. Lastly this Feynman diagram has the time and space axes reversed. What do you think?