1) If you go to the Redmond Air Show in the summer you may have an opportunity to apply the Doppler shift to the sounds of jets as they fly towards you. If the frequency you observe as the jet flies towards you is 50% higher than that when it passes overhead how fast is the jet going? Assume the speed of sound is 343 m/s in air.
[114 m/s]
2) Astronomers observe the red light (656 nm = λ) from hydrogen. This light is observed to be redshifted (moved to longer wavelengths) in astronomical objects from which we are receding. If we are receding from a galaxy at 25% of the speed of light (speed of light = c =3.108 m/s) what is the wavelength of red light emitted by the galaxy that we will observe? Does it matter if we are receding from the galaxy or it is receding from us?
[875 nm - yes it matters]
3) I have three tuning forks (A, B, and C) which produce slightly different frequencies. When A and B are sounded together a 2 Hz beat frequency is heard. When A and C are sounded together a 5 Hz beat is heard. What beat frequency will be heard when B and C are sounded together? (there are two answers!)
[3 Hz or 7 Hz]
4) As I drive down from Mt Hood my entire instrument panel in the car fails along with my brakes. As a accelerate down the winding road I wonder what to do. In desperation I lay on the horn which happens to produce a pitch I recognize as 392 Hz. Instead of calling to police in response to my obnoxious behavior the person in the identical car parked along the road blows their horn (also at 392 Hz due to manufacturing consistency) in a futile gesture of solidarity. The combined effect of the two horns produces a beat frequency of 60 Hz which I hear as a low pitch. As I hurtle towards my fate I frantically calculate my speed based on the beat frequency and Doppler shift ideas. What speed do I calculate?
[52 m/s]
5) Suppose bats have a social need for police to enforce a speed limit because too many teenage bats are crashing into trees that they could have avoided. A Bat Patrol (BP) is formed and is trained to use doppler shifting of their squeaks to determine bat speeds. Officer Barney (BP 302) observes that the reflection of his calibrated (40,000 Hz) squeak from Tony Teenbat is up by 3500 Hz as Tony approaches him. Barney is flying at his normal cruising speed of 4.5 m/s. What is Tony's speed?
[20.2 m/s]
6) Another problem from the “Why would I do that?” pile. Imagine you are accelerating towards a stationary source of sound that produces a frequency of 800 Hz. You notice that the frequency you observe increases by 28 Hz over 4 s. What is your acceleration based on this data? Assume your acceleration is constant. (your knowledge of calculus will be useful here!)
[3 m/s/s]
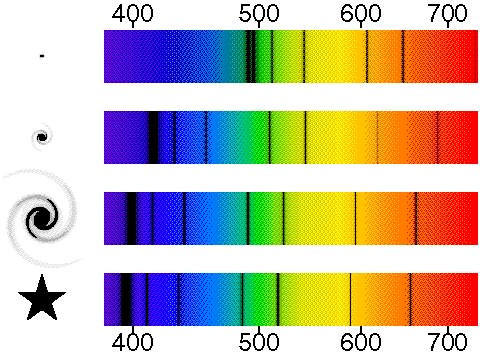
7) Here's another example that needs you to consider the data and be sure you understand how to use it in this context. I keep mentioning that astronomers use redshift to determine how fast galaxies are moving relative to us. Here is some real data starting, at the bottom, with a star which is NOT moving relative to us. Determine how fast each galaxy is moving and whether they are approaching or receding from us. In case you are wondering the things to the left of the spectra are the galaxies starting with the most distant at the top.