This homework set has historically been a bit long so I am reducing the number of problems and asking slightly different questions in hopes this will help you make more sense of the connection between the physical settings and the mathematical descriptions.

1) A 200 g mass on a horizontal spring oscillates about x=0 with a frequency of 2 Hz. Its total range of motion is 5 cm At t=0 the mass is at x=0 and the velocity at the origin is in the positive direction. Assume the motion can be described by a sine or cosine function. Begin by sketching a position vrs time plot for this motion on graph paper that shows 2 complete cycles of the mass. Put your name on the graph and exchange it with someone else in the class you don't normally work with. You may do this with hardcopies or by sharing decent images with each other -- be sure your name shows on the plot. Using the plot you have been given by your peer determine the following features of the motion:

a) the period and frequency of the motion

b) the amplitude of motion

c) the maximum velocity along with the times and locations at which it takes place

d) the maximum acceleration along with the times and locations at which it takes place

e) the displacement and velocity at t=.4s

 

[.5 s, 2 Hz, 2.5 cm, 31 cm/s, 4 (m/s)/s, -2.4 cm]

2) Refer to the following plot of the behavior of an object. Even though this is not a sine or cosine (harmonic) function the labels for the various features still apply.

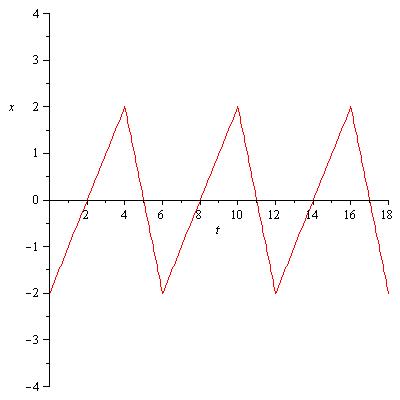
a) Is this motion periodic? What is the period if there is one?

b) Is this simple harmonic motion? Why or why not?

c) What is the amplitude of this motion? What is the frequency?

d) Sketch the velocity vrs time plot and determine the maximum velocity.

[yes, 6 s, no, cuz, 2 m, .17 Hz, 2.0 m/s]

3) The graph shows the potential energy and the total energy of a 250 g mass moving periodically, horizontally, on a spring.

a) Where is the mass when the spring is unstretched?

b) Where is the mass when it changes direction? How did you figure this out?

c) What is the maximum kinetic energy of the mass?

d) What is the maximum velocity of the mass?

[0, 10 cm, 8 J, 8 m/s]

4) Consider this sunspot data. While it may not be perfectly periodic how would you best model it as periodic behavior? Think about what you have to do to deal with 0 sunspots NOT being the equilibrium state of the graph. You will need to decide when to set your time equal to zero. You will also need to make a decision about how to deal with the inconsistent "amplitude" of this periodic behavior. Do this both for the period from about 1880 - 1920 as well as the period from 1960 to the present. Are there differences and if so what are they? Exchange your model with a friend in the class (different person from problem 1) and use the new model to calculate the years of sunspot maxima between 2040 and 2060.

[-40cos((2π/11.3yrs)t +40]

5) Two blocks with the masses shown are moving in SHM on a frictionless table. The coefficient of friction between the blocks is 0.40 and the spring constant is 200 N/m. Next week we will learn how to determine the period from the differential equation but for now you can take it to be 1.4 s. What do you expect to happen to the period if the 10 kg mass is increased? Why? What do you expect to happen to the period if the spring constant is increased? Why? What is the maximum amplitude of the oscillation where the blocks do not move relative to each other? What is the maximum kinetic energy of the system? (You'll need to do a freebody and use Newton's Laws as well as the new material)

[22 cm, 4.8 J]

 

6) The following plot shows an object experiencing damped periodic motion. Assume that the vertical axis is labelled in m. Estimate the maximum velocity at each succesive point where the curve passes through the equilibrium point. Use the tools we have developed for well behaved periodic motion. You should be able to get 5 data points off the plot. For each one determine the kinetic energy of the 100g mass which this plot represents. (do so!). Is the loss of kinetic energy constant from point to point? Can you tell if the rate of change of the kinetic energy is a constant percentage of the previous data point?

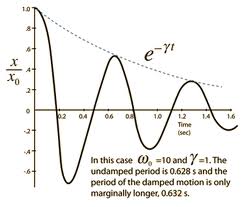
7) If I "pump" this mass by adding 0.5 J of energy to each cycle what will happen? There are, as usual, several ways you can think about this. If I start pumping from the very begining what will happen? If I start pumping the system after 4 seconds what will happen? What would happen if there were no damping in the system while I was pumping it. These are qualitative questions that test your understanding of question 6).