Throughout this problem set you are going to be challenged to create effective sketches of the setings. Learning what to sketch and how to explore the problem at this conceptual level is an important part of what we are learning in this section.

1) You are 1.6 m tall and need to hang a mirror on the wall so that you can see yourself from head to toe. How tall does the mirror need to be and where do you need to stand to see yourself from head to toe? (Law of Reflection)

[.8 m]

2) Consider a coin in the bottom of a bucket whose depth is d. Show that your eyes perceive the light to be coming from a point d*= d/n below the surface of the water. Consider the paths of light leaving a point in the center of the coin.   [look at where the exiting rays intersect under the surface]

 

3) A plate glass window (n=1.5) is cast so that it is tapered at a 5 degree angle. You are looking through such a window at an angle of 30 degrees with respect to the normal and see a person standing there. If the person is standing 2 m from the window how far off your line of sight are they really standing as opposed to where they appear to be? Such windows could potentially be used in security applications.

[13 cm to side]

4) A right prism is a columnar piece of glass whose cross section is a equilateral (actually isoceles) right triangle. Light enters the prism at an angle θ ₁ as shown and exits the second surface at an angle of 90 degrees. What is the maximum possible value of the index of refraction of the glass in terms of the angle θ? What happens if n is greater than this value? Be aware that this graphic shows a prism which is NOT a right triangle. In our problem the apex angle at the top is 90^o .

[n=(sin²θ+1)^0.5]

5) Imagine a hemi-spherical mirror with the concave side facing a light source. Draw a line perpendicular to the center of the mirror - this is called the optical axis of the mirror and defines the direction it points. Consider the behavior of light which is travelling parallel to this optic axis towards the spherical mirror and hits it at some distance d from the axis. Where, relative to the center of the sphere, will the light cross the optic axis?

[at R/2 from bottom of hemisphere]

6) Imagine a sphere of glass of index 1.5. Draw a line perpendicular to some point of that sphere (which looks like a circle in cross section). Extend this line inwards until it reaches the center of the sphere. This is the optic axis of the sphere (similar to the previous problem) Consider the behavior of light which is travelling parallel to this optic axis towards the sphere and hits it at some distance d from the axis. Where, relative to the center of the sphere will the light cross the optic axis?

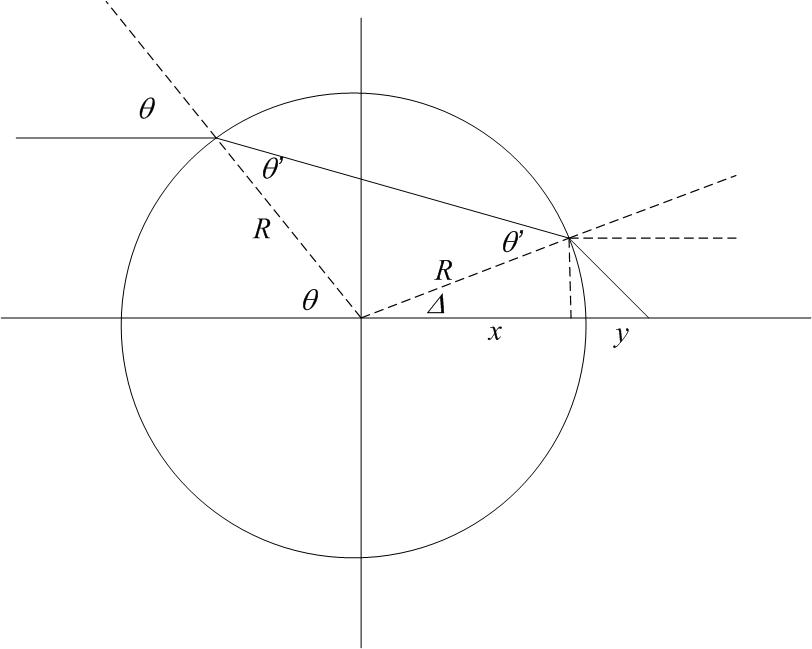
[very complex expression - ask in class]