1) Blowing across the top of a soda bottle produces a loud low pitched sound. Explain why the pitch of this sound is higher when the bottle is partially filled with water. (there are physics reasons that have to do with standing wave patterns -- if you want to get more precise you can refer to discussions of Helmholtz resonators)

2) The resonator tube under the lowest note of a marimba (a common performance instrument at Bend festivals) is 85 cm long and open at the bottom end. What does the physics of standing waves say about the lowest resonant frequency of this tube?

[202 Hz]

3) The marimba bar over the resonator in 2) is 40 cm long and is supported 10 cm from each end. If the frequency of the sound produced by the bar is actually 200 Hz what is the speed of the wave traveling up and down the marimba bar?

[81 m/s]

In the following two questions it may be helpful to know that the strings in a piano are all under about the same tension to prevent warping of the frame of the piano. In general both the length of the strings and their diameter varies.

4) The lowest note on the piano is 27.5 Hz (if it is officially tuned) which is produced by a string 1.18 m long. There are two waves involved here, the standing wave on the string and the sound wave produced by the string pounding on the air. What is the ratio of the wavelength of the sound produced to the wavelength of the wave propagating on the string?

[5.3]

5) As stated previously the lowest note on the piano is 27.5 Hz and is produced by a string 1.18 m long. If, for efficiency of manufacturing, the same wire is used to produce the highest pitch on the piano (5096 Hz) how long would this string be? Does this seem like a sensible way to build a piano? Find a piano and peer into it -- how do they solve this problem and what is the physics behind it?

[6.4 mm - way too short, use smaller wire]

6) Your barbershop quartet is on a trip together and find yourselves at the entrance of a tunnel where you can't see the other end. Knowing that tunnels give great resonances you try singing into the tunnel. After much experimentation you find that an inverted D7 chord really makes the tunnel sing (resonate!). The frequencies in this chord are 110 Hz, 130 Hz, and 145 Hz. These must be standing wave frequencies of the tunnel but they are not necessarily all the frequencies or even successive frequencies. What is the shortest possible length of the tunnel consistent with this data? ( Hint: look at the ratios of the frequencies)

[34.3 m]

7) A flute has successive resonant frequencies at 260 Hz, 520 Hz, 780 Hz, and 1040 Hz. Does this suggest that the flute behaves like a tube open at only one end or a tube open at both ends? Explain your reasoning.

[symmetric boundary conditions]

8) The lowest string of the guitar is intended to have a fundamental frequency of approximately 161 Hz. The highest string on the guitar has a fundamental frequency of 645 Hz. In order to avoid nonuniform strains in the neck of the guitar all strings should be under the same tension. What is the ratio of the mass of the lowest string to that of the highest string?

[16]

9) This is one of those problems that fascinate me and an old test problem. You are confronted with a box 2.4 m long with a rope hanging out of a hole at one end. The rope outside the box is 1.2 m long and the box has a transparent top so you can see that the rope is tied to the other end of the box. Along the side of the box are a number of switches that you need to turn on in a particular order to win the $1^.10⁶ prize. The switches must be turned on in alphabetical order. Once the switch has been turned on it stays on so you don't have to worry about hitting it again. You can generate standing waves in the box by shaking the rope outside the box. Where you hold the rope will be a node but you don't have to hold it at the end.

I) What is the shape of the standing wave, inside and outside the box, you could use to turn on switch A without turning on any others?

II) If the speed of the wave is observed to be 4 m/s what is the frequency of the standing wave which turns on switch B (but not C)? Sketch the wave both inside and outside the box.

III) What is the shape, inside and outside the box, and frequency of the wave which you could use to turn on switch C? Are there other switches that will be hit? Sketch what has to happen in the box and be prepared to shorten your grip on the rope outside the box for this!

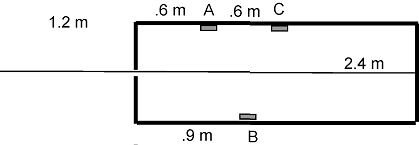
[λ =2.4 m, f= 3.33 Hz, λ = 1.6 m]