1) Light travels at 3^.10⁸ m/s in air. The wavelength of red light is around 660 nm (depending on which color red). What is the frequency of the red light?

[4.5^.10¹⁴ Hz]

2) It is sometimes said that person “can not hear sound whose wavelength is larger that the size of your ear”. Test the veracity of this statement given that the speed of sound in air is 343 m/s and the human ear can usually hear sounds from 20 Hz to 20,000 Hz. (As we get older we tend to lose sensitivity on the high frequency end as you will notice next week)

[17 m - 1.7 cm for l]

3) Suppose the speed of light were 598 m/s instead of 3^.10⁸ m/s, but the speed of sound remained the same at 343 m/s. How would you need to modify the 5 second rule for lightning bolts to allow accurate estimation of the distance?

[2 s/mile or 1.3 s/km]

4) The wavelength of sound in air is 2.74 m. As the sound runs into the surface of a pond the wave is transmitted into the water. What is the wavelength of the sound in the water? Assume the speed of sound in air to be 343 m.s and that of sound in water to be 1480 m/s if you need to.

[11.8 m]

5) Imaging specialists know that it is not possible to “see” an object if the object is smaller than the wavelength of the “light” that you shine on it. Bats use sound (squeaks) to “see” the insects which are their prey and the same imaging rule applies to sound. Based on your intimate knowledge of insects what is the minimum frequency of a bat squeak needed to accurately located insects? It is known that bats that hunt larger prey have lower frequency squeaks. Sometimes I wonder about the squeaks of the fabled Alaskan saber-toothed cave bat from the late Pleistocene given the probably size of ancient Alaskan mosquitos. Are you bothered by the assertion that this rule is true (it is!) and the one in problem 3 is not?

[20-60 kHz depending on size of "bug"]

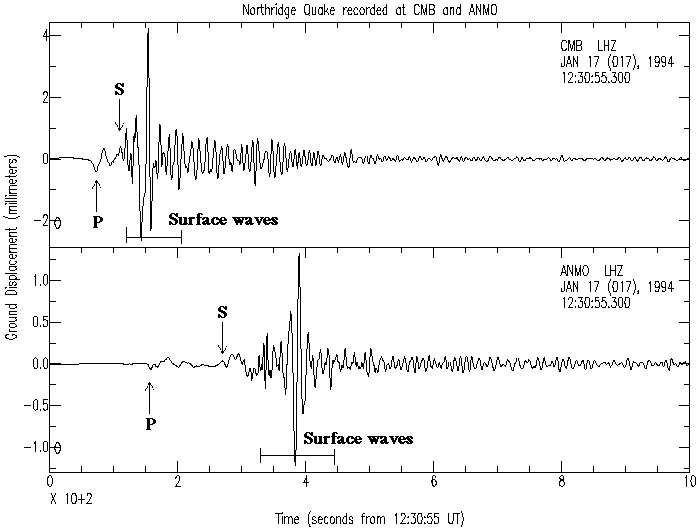
6) Here's a real life (and challenging) question. The seismic data below was recorded at Columbia, CA and Albuquerque, NM respectively. As you can see from the data the arrival times for the P and S waves are different for each location. Based on this data and the assumption that the P and S waves have the consistent velocities what is the speed of each wave?

There are many things I am 'testing' with this problem. It is a variation of the thunder and lightning calculation. For some discussion of this stuff take a look at this website. Here's another source that includes a range of wave speeds. What wave speed should you use? Why do you need to know where the data was recorded? Can you understand the plots? Does your data confirm the location of the earthquake in Northridge CA?.

7) Consider a pulse, a wavelet, traveling up a hanging rope. As you have noticed in our class explorations the speed of the wave depends on the characteristics of the medium carrying the wave. What characteristics of the rope could affect the speed of the wave as it travels along. Confirm your understanding this one page pdf on the speed of waves in ropes. [Thanks to the Caltech Physic League for this short paper!]You will need to read carefully since the paper uses slightly different language at points. The last expression is the one you need to understand.

Given the critical engineering information you have gleaned from your observation of ropes and the paper we now apply it to a hanging rope. Which of the factors affecting the wave speed change at different points on a uniform hanging rope? Now you have all the pieces you need. Calculate the time it takes for a pulse to travel up a hanging rope of mass 2.5 kg and length 9.5 m. This is a calculus problem that involves freebody diagrams to start and clear setup to get the integral. Doing the integral is pretty easy it's setting it up that's the challenge!

[1.95 s]