
The Mars Climate Orbiter is prepared for its mission. The laws of physics are the same everywhere, even on Mars, so the probe could be designed based on the laws of physics as discovered on earth. There is unfortunately another reason why this spacecraft is relevant to the topics of this chapter: it was destroyed attempting to enter Mars' atmosphere because engineers at Lockheed Martin forgot to convert data on engine thrusts from pounds into the metric unit of force (newtons) before giving the information to NASA. Conversions are important!
Chapter 0. Introduction and Review
0.1 The Scientific Method

a / Science is a cycle of theory and experiment.

b / A satirical drawing of an alchemist's laboratory. H. Cock, after a drawing by Peter Brueghel the Elder (16th century).
Until very recently in history, no progress was made in answering questions like these. Worse than that, the wrong answers written by thinkers like the ancient Greek physicist Aristotle were accepted without question for thousands of years. Why is it that scientific knowledge has progressed more since the Renaissance than it had in all the preceding millennia since the beginning of recorded history? Undoubtedly the industrial revolution is part of the answer. Building its centerpiece, the steam engine, required improved techniques for precise construction and measurement. (Early on, it was considered a major advance when English machine shops learned to build pistons and cylinders that fit together with a gap narrower than the thickness of a penny.) But even before the industrial revolution, the pace of discovery had picked up, mainly because of the introduction of the modern scientific method. Although it evolved over time, most scientists today would agree on something like the following list of the basic principles of the scientific method:
(1) Science is a cycle of theory and experiment. Scientific theories are created to explain the results of experiments that were created under certain conditions. A successful theory will also make new predictions about new experiments under new conditions. Eventually, though, it always seems to happen that a new experiment comes along, showing that under certain conditions the theory is not a good approximation or is not valid at all. The ball is then back in the theorists' court. If an experiment disagrees with the current theory, the theory has to be changed, not the experiment.
(2) Theories should both predict and explain. The requirement of predictive power means that a theory is only meaningful if it predicts something that can be checked against experimental measurements that the theorist did not already have at hand. That is, a theory should be testable. Explanatory value means that many phenomena should be accounted for with few basic principles. If you answer every “why” question with “because that's the way it is,” then your theory has no explanatory value. Collecting lots of data without being able to find any basic underlying principles is not science.
(3) Experiments should be reproducible. An experiment should be treated with suspicion if it only works for one person, or only in one part of the world. Anyone with the necessary skills and equipment should be able to get the same results from the same experiment. This implies that science transcends national and ethnic boundaries; you can be sure that nobody is doing actual science who claims that their work is “Aryan, not Jewish,” “Marxist, not bourgeois,” or “Christian, not atheistic.” An experiment cannot be reproduced if it is secret, so science is necessarily a public enterprise.
As an example of the cycle of theory and experiment, a vital step toward modern chemistry was the experimental observation that the chemical elements could not be transformed into each other, e.g., lead could not be turned into gold. This led to the theory that chemical reactions consisted of rearrangements of the elements in different combinations, without any change in the identities of the elements themselves. The theory worked for hundreds of years, and was confirmed experimentally over a wide range of pressures and temperatures and with many combinations of elements. Only in the twentieth century did we learn that one element could be trans-formed into one another under the conditions of extremely high pressure and temperature existing in a nuclear bomb or inside a star. That observation didn't completely invalidate the original theory of the immutability of the elements, but it showed that it was only an approximation, valid at ordinary temperatures and pressures.
self-check: A psychic conducts seances in which the spirits of the dead speak to the participants. He says he has special psychic powers not possessed by other people, which allow him to “channel” the communications with the spirits. What part of the scientific method is being violated here? (answer in the back of the PDF version of the book)
The scientific method as described here is an idealization, and should not be understood as a set procedure for doing science. Scientists have as many weaknesses and character flaws as any other group, and it is very common for scientists to try to discredit other people's experiments when the results run contrary to their own favored point of view. Successful science also has more to do with luck, intuition, and creativity than most people realize, and the restrictions of the scientific method do not stifle individuality and self-expression any more than the fugue and sonata forms stifled Bach and Haydn. There is a recent tendency among social scientists to go even further and to deny that the scientific method even exists, claiming that science is no more than an arbitrary social system that determines what ideas to accept based on an in-group's criteria. I think that's going too far. If science is an arbitrary social ritual, it would seem difficult to explain its effectiveness in building such useful items as airplanes, CD players and sewers. If alchemy and astrology were no less scientific in their methods than chemistry and astronomy, what was it that kept them from producing anything useful?
Discussion Questions
withintro{Consider whether or not the scientific method is being applied in the following examples. If the scientific method is not being applied, are the people whose actions are being described performing a useful human activity, albeit an unscientific one? }
◊ Acupuncture is a traditional medical technique of Asian origin in which small needles are inserted in the patient's body to relieve pain. Many doctors trained in the west consider acupuncture unworthy of experimental study because if it had therapeutic effects, such effects could not be explained by their theories of the nervous system. Who is being more scientific, the western or eastern practitioners?
◊ Goethe, a German poet, is less well known for his theory of color. He published a book on the subject, in which he argued that scientific apparatus for measuring and quantifying color, such as prisms, lenses and colored filters, could not give us full insight into the ultimate meaning of color, for instance the cold feeling evoked by blue and green or the heroic sentiments inspired by red. Was his work scientific?
◊ A child asks why things fall down, and an adult answers “because of gravity.” The ancient Greek philosopher Aristotle explained that rocks fell because it was their nature to seek out their natural place, in contact with the earth. Are these explanations scientific?
◊ Buddhism is partly a psychological explanation of human suffering, and psychology is of course a science. The Buddha could be said to have engaged in a cycle of theory and experiment, since he worked by trial and error, and even late in his life he asked his followers to challenge his ideas. Buddhism could also be considered reproducible, since the Buddha told his followers they could find enlightenment for themselves if they followed a certain course of study and discipline. Is Buddhism a scientific pursuit?
0.2 What Is Physics?
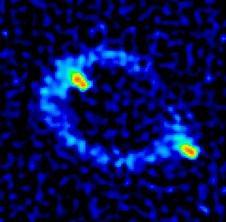
c / This telescope picture shows two images of the same distant object, an exotic, very luminous object called a quasar. This is interpreted as evidence that a massive, dark object, possibly a black hole, happens to be between us and it. Light rays that would otherwise have missed the earth on either side have been bent by the dark object's gravity so that they reach us. The actual direction to the quasar is presumably in the center of the image, but the light along that central line doesn't get to us because it is absorbed by the dark object. The quasar is known by its catalog number, MG1131+0456, or more informally as Einstein's Ring.
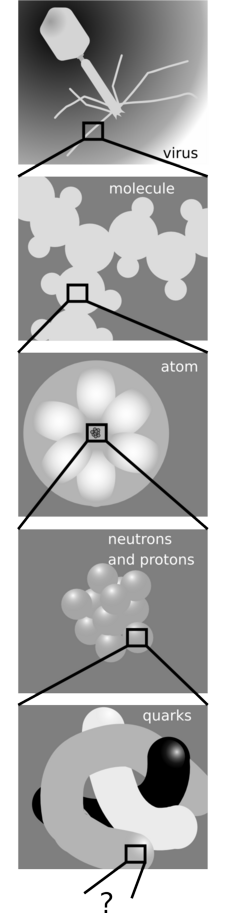
d / Reductionism.
Given for one instant an intelligence which could comprehend all the forces by which nature is animated and the respective positions of the things which compose it...nothing would be uncertain, and the future as the past would be laid out before its eyes. -- Pierre Simon de Laplace
Physics is the use of the scientific method to find out the basic principles governing light and matter, and to discover the implications of those laws. Part of what distinguishes the modern outlook from the ancient mind-set is the assumption that there are rules by which the universe functions, and that those laws can be at least partially understood by humans. From the Age of Reason through the nineteenth century, many scientists began to be convinced that the laws of nature not only could be known but, as claimed by Laplace, those laws could in principle be used to predict everything about the universe's future if complete information was available about the present state of all light and matter. In subsequent sections, I'll describe two general types of limitations on prediction using the laws of physics, which were only recognized in the twentieth century.
Matter can be defined as anything that is affected by gravity, i.e., that has weight or would have weight if it was near the Earth or another star or planet massive enough to produce measurable gravity. Light can be defined as anything that can travel from one place to another through empty space and can influence matter, but has no weight. For example, sunlight can influence your body by heating it or by damaging your DNA and giving you skin cancer. The physicist's definition of light includes a variety of phenomena that are not visible to the eye, including radio waves, microwaves, x-rays, and gamma rays. These are the “colors” of light that do not happen to fall within the narrow violet-to-red range of the rainbow that we can see.
self-check: At the turn of the 20th century, a strange new phenomenon was discovered in vacuum tubes: mysterious rays of unknown origin and nature. These rays are the same as the ones that shoot from the back of your TV's picture tube and hit the front to make the picture. Physicists in 1895 didn't have the faintest idea what the rays were, so they simply named them “cathode rays,” after the name for the electrical contact from which they sprang. A fierce debate raged, complete with nationalistic overtones, over whether the rays were a form of light or of matter. What would they have had to do in order to settle the issue? (answer in the back of the PDF version of the book)
Many physical phenomena are not themselves light or matter, but are properties of light or matter or interactions between light and matter. For instance, motion is a property of all light and some matter, but it is not itself light or matter. The pressure that keeps a bicycle tire blown up is an interaction between the air and the tire. Pressure is not a form of matter in and of itself. It is as much a property of the tire as of the air. Analogously, sisterhood and employment are relationships among people but are not people themselves.
Some things that appear weightless actually do have weight, and so qualify as matter. Air has weight, and is thus a form of matter even though a cubic inch of air weighs less than a grain of sand. A helium balloon has weight, but is kept from falling by the force of the surrounding more dense air, which pushes up on it. Astronauts in orbit around the Earth have weight, and are falling along a curved arc, but they are moving so fast that the curved arc of their fall is broad enough to carry them all the way around the Earth in a circle. They perceive themselves as being weightless because their space capsule is falling along with them, and the floor therefore does not push up on their feet.
Optional topic: Optional Topic: Modern Changes in the Definition of Light and Matter
Einstein predicted as a consequence of his theory of relativity that light would after all be affected by gravity, although the effect would be extremely weak under normal conditions. His prediction was borne out by observations of the bending of light rays from stars as they passed close to the sun on their way to the Earth. Einstein's theory also implied the existence of black holes, stars so massive and compact that their intense gravity would not even allow light to escape. (These days there is strong evidence that black holes exist.)
Einstein's interpretation was that light doesn't really have mass, but that energy is affected by gravity just like mass is. The energy in a light beam is equivalent to a certain amount of mass, given by the famous equation E=mc2, where c is the speed of light. Because the speed of light is such a big number, a large amount of energy is equivalent to only a very small amount of mass, so the gravitational force on a light ray can be ignored for most practical purposes.
There is however a more satisfactory and fundamental distinction between light and matter, which should be understandable to you if you have had a chemistry course. In chemistry, one learns that electrons obey the Pauli exclusion principle, which forbids more than one electron from occupying the same orbital if they have the same spin. The Pauli exclusion principle is obeyed by the subatomic particles of which matter is composed, but disobeyed by the particles, called photons, of which a beam of light is made.
Einstein's theory of relativity is discussed more fully in book 6 of this series.
The boundary between physics and the other sciences is not always clear. For instance, chemists study atoms and molecules, which are what matter is built from, and there are some scientists who would be equally willing to call themselves physical chemists or chemical physicists. It might seem that the distinction between physics and biology would be clearer, since physics seems to deal with inanimate objects. In fact, almost all physicists would agree that the basic laws of physics that apply to molecules in a test tube work equally well for the combination of molecules that constitutes a bacterium. (Some might believe that something more happens in the minds of humans, or even those of cats and dogs.) What differentiates physics from biology is that many of the scientific theories that describe living things, while ultimately resulting from the fundamental laws of physics, cannot be rigorously derived from physical principles.
Isolated systems and reductionism
Discussion Questions
0.3 How to Learn Physics
0.4 Self-Evaluation
|
If you disagree with this statement. . . |
you should study this section: |
|
I am familiar with the basic metric units of meters, kilograms, and seconds, and the most common metric prefixes: milli- (m), kilo- (k), and centi- (c). |
0.5 Basic of the Metric System |
|
I know about the newton, a unit of force |
0.6 The newton, the Metric Unit of Force |
|
I am familiar with these less common metric prefixes: mega- (M), micro- (μ), and nano- (n). |
0.7 Less Common Metric Prefixes |
|
I am comfortable with scientific notation. |
0.8 Scientific Notation |
|
I can confidently do metric conversions. |
0.9 Conversions |
|
I understand the purpose and use of significant figures. |
0.10 Significant Figures |
0.5 Basics of the Metric System

e / Pope Gregory created our modern Gregorian calendar, with its system of leap years, to make the length of the calendar year match the length of the cycle of seasons. Not until 1752 did Protestant England switched to the new calendar. Some less educated citizens believed that the shortening of the month by eleven days would shorten their lives by the same interval. In this illustration by William Hogarth, the leaflet lying on the ground reads, “Give us our eleven days.”
f / The original definition of the meter.
The metric system
The following are the most common metric prefixes. You should memorize them.
prefix
|
meaning | example
|
||
| kilo- | k | 103 | 60 kg |
= a person’s mass |
| centi- | c | 10-2 | 28 cm |
= height of a piece of paper |
| milli- | m | 10-3 | 1 ms |
= time for one vibration of a guitar string playing the note D |
The second
The meter
The kilogram
Combinations of metric units
Discussion Question
0.6 The Newton, the Metric Unit of Force
In section 0.5, I gave a gravitational definition of mass, but by defining a numerical scale of force, we can also turn around and define a scale of mass without reference to gravity. For instance, if a force of two Newtons is required to accelerate a certain object from rest to 1 m/s in 1 s, then that object must have a mass of 2 kg. From this point of view, mass characterizes an object's resistance to a change in its motion, which we call inertia or inertial mass. Although there is no fundamental reason why an object's resistance to a change in its motion must be related to how strongly gravity affects it, careful and precise experiments have shown that the inertial definition and the gravitational definition of mass are highly consistent for a variety of objects. It therefore doesn't really matter for any practical purpose which definition one adopts.
Discussion Question
◊ Spending a long time in weightlessness is unhealthy. One of the most important negative effects experienced by astronauts is a loss of muscle and bone mass. Since an ordinary scale won't work for an astronaut in orbit, what is a possible way of monitoring this change in mass? (Measuring the astronaut's waist or biceps with a measuring tape is not good enough, because it doesn't tell anything about bone mass, or about the replacement of muscle with fat.)
0.7 Less Common Metric Prefixes
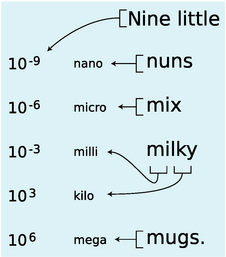
g / This is a mnemonic to help you remember the most important metric prefixes. The word “little” is to remind you that the list starts with the prefixes used for small quantities and builds upward. The exponent changes by 3, except that of course that we do not need a special prefix for 100, which equals one.
The following are three metric prefixes which, while less common than the ones discussed previously, are well worth memorizing.
prefix
|
meaning | example
|
||
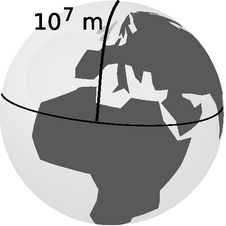
| mega- | M | 106 | 6.4 Mm |
= radius of the earth |
| micro- | μ | 10-6 | 10 μm |
= size of a white blood cell |
| nano- | n | 10-9 | 0.154 nm |
= distance between carbon nuclei in an ethane molecule |
Note that the abbreviation for micro is the Greek letter mu, μ --- a common mistake is to confuse it with m (milli) or M (mega).
There are other prefixes even less common, used for extremely large and small quantities. For instance, 1 femtometer=10-15 m is a convenient unit of distance in nuclear physics, and 1 gigabyte=109 bytes is used for computers' hard disks. The international committee that makes decisions about the SI has recently even added some new prefixes that sound like jokes, e.g.,  is about half the mass of a proton. In the immediate future, however, you're unlikely to see prefixes like “yocto-” and “zepto-” used except perhaps in trivia contests at science-fiction conventions or other geekfests.
is about half the mass of a proton. In the immediate future, however, you're unlikely to see prefixes like “yocto-” and “zepto-” used except perhaps in trivia contests at science-fiction conventions or other geekfests.
self-check: Suppose you could slow down time so that according to your perception, a beam of light would move across a room at the speed of a slow walk. If you perceived a nanosecond as if it was a second, how would you perceive a microsecond? (answer in the back of the PDF version of the book)
0.8 Scientific Notation
Each number is ten times bigger than the previous one.
A common source of confusion is the notation used on the displays of many calculators. Examples:
| 3.2 × 106 | (written notation) |
| 3.2E+6 | (notation on some calculators) |
| 3.26 | (notation on some other calculators) |
The student concludes that 102 bacteria would form a line of this length:
Why is the student incorrect? (answer in the back of the PDF version of the book)
0.9 Conversions
To convert grams to kilograms, you would simply flip the fraction upside down.
Should that exponent be positive or negative?
A common mistake is to write the conversion fraction incorrectly. For instance the fraction
| big prefixes: | k M |
| small prefixes: | m μ n |
◊ Solved problem: a simple conversion — problem 6
◊ Solved problem: the geometric mean — problem 8
Discussion Question
◊ Each of the following conversions contains an error. In each case, explain what the error is.
0.10 Significant Figures
An engineer is designing a car engine, and has been told that the diameter of the pistons (which are being designed by someone else) is 5 cm. He knows that 0.02 cm of clearance is required for a piston of this size, so he designs the cylinder to have an inside diameter of 5.04 cm. Luckily, his supervisor catches his mistake before the car goes into production. She explains his error to him, and mentally puts him in the “do not promote” category.
What was his mistake? The person who told him the pistons were 5 cm in diameter was wise to the ways of significant figures, as was his boss, who explained to him that he needed to go back and get a more accurate number for the diameter of the pistons. That person said “5 cm” rather than “5.00 cm” specifically to avoid creating the impression that the number was extremely accurate. In reality, the pistons' diameter was 5.13 cm. They would never have fit in the 5.04-cm cylinders.
The number of digits of accuracy in a number is referred to as the number of significant figures, or “sig figs” for short. As in the example above, sig figs provide a way of showing the accuracy of a number. In most cases, the result of a calculation involving several pieces of data can be no more accurate than the least accurate piece of data. In other words, “garbage in, garbage out.” Since the 5 cm diameter of the pistons was not very accurate, the result of the engineer's calculation, 5.04 cm, was really not as accurate as he thought. In general, your result should not have more than the number of sig figs in the least accurate piece of data you started with. The calculation above should have been done as follows:



The fact that the final result only has one significant figure then alerts you to the fact that the result is not very accurate, and would not be appropriate for use in designing the engine.
Note that the leading zeroes in the number 0.04 do not count as significant figures, because they are only placeholders. On the other hand, a number such as 50 cm is ambiguous --- the zero could be intended as a significant figure, or it might just be there as a placeholder. The ambiguity involving trailing zeroes can be avoided by using scientific notation, in which 5×101 cm would imply one sig fig of accuracy, while 5.0×101 cm would imply two sig figs.
self-check: The following quote is taken from an editorial by Norimitsu Onishi in the New York Times, August 18, 2002.
What should bother you about this? (answer in the back of the PDF version of the book)
Dealing correctly with significant figures can save you time! Often, students copy down numbers from their calculators with eight significant figures of precision, then type them back in for a later calculation. That's a waste of time, unless your original data had that kind of incredible precision.
The rules about significant figures are only rules of thumb, and are not a substitute for careful thinking. For instance, $20.00 + $0.05 is $20.05. It need not and should not be rounded off to $20. In general, the sig fig rules work best for multiplication and division, and we also apply them when doing a complicated calculation that involves many types of operations. For simple addition and subtraction, it makes more sense to maintain a fixed number of digits after the decimal point.
When in doubt, don't use the sig fig rules at all. Instead, intentionally change one piece of your initial data by the maximum amount by which you think it could have been off, and recalculate the final result. The digits on the end that are completely reshuffled are the ones that are meaningless, and should be omitted.
self-check: How many significant figures are there in each of the following measurements?
(1) 9.937 m
(2) 4.0 s
(3) 0.0000000000000037 kg (answer in the back of the PDF version of the book)
Summary
Vocabulary
matter — Anything that is affected by gravity.
Système International — A fancy name for the metric system.
mass — A numerical measure of how difficult it is to change an object's motion.
significant figures — Digits that contribute to the accuracy of a measurement.
Homework Problems
1. Correct use of a calculator: (a) Calculate  on a calculator. [Self-check: The most common mistake results in 97555.40.] (answer check available at lightandmatter.com)
on a calculator. [Self-check: The most common mistake results in 97555.40.] (answer check available at lightandmatter.com)
(b) Which would be more like the price of a TV, and which would be more like the price of a house, $3.5×105 or $3.55?
2. Compute the following things. If they don't make sense because of units, say so.
(a) 3 cm + 5 cm
(b) 1.11 m + 22 cm
(c) 120 miles + 2.0 hours
(d) 120 miles / 2.0 hours
3. Your backyard has brick walls on both ends. You measure a distance of 23.4 m from the inside of one wall to the inside of the other. Each wall is 29.4 cm thick. How far is it from the outside of one wall to the outside of the other? Pay attention to significant figures.
4. The speed of light is 3.0×108 m/s. Convert this to furlongs per fortnight. A furlong is 220 yards, and a fortnight is 14 days. An inch is 2.54 cm.(answer check available at lightandmatter.com)
5. Express each of the following quantities in micrograms:
(a) 10 mg, (b) 104 g, (c) 10 kg, (d) 100×103 g, (e) 1000 ng. (answer check available at lightandmatter.com)
6. (solution in the pdf version of the book) Convert 134 mg to units of kg, writing your answer in scientific notation.
7. In the last century, the average age of the onset of puberty for girls has decreased by several years. Urban folklore has it that this is because of hormones fed to beef cattle, but it is more likely to be because modern girls have more body fat on the average and possibly because of estrogen-mimicking chemicals in the environment from the breakdown of pesticides. A hamburger from a hormone-implanted steer has about 0.2 ng of estrogen (about double the amount of natural beef). A serving of peas contains about 300 ng of estrogen. An adult woman produces about 0.5 mg of estrogen per day (note the different unit!). (a) How many hamburgers would a girl have to eat in one day to consume as much estrogen as an adult woman's daily production? (b) How many servings of peas? (answer check available at lightandmatter.com)
8. (solution in the pdf version of the book) The usual definition of the mean (average) of two numbers a and b is (a+b)/2. This is called the arithmetic mean. The geometric mean, however, is defined as (ab)1/2 (i.e., the square root of ab). For the sake of definiteness, let's say both numbers have units of mass. (a) Compute the arithmetic mean of two numbers that have units of grams. Then convert the numbers to units of kilograms and recompute their mean. Is the answer consistent? (b) Do the same for the geometric mean. (c) If a and b both have units of grams, what should we call the units of ab? Does your answer make sense when you take the square root? (d) Suppose someone proposes to you a third kind of mean, called the superduper mean, defined as (ab)1/3. Is this reasonable?
9. In an article on the SARS epidemic, the May 7, 2003 New York Times discusses conflicting estimates of the disease's incubation period (the average time that elapses from infection to the first symptoms). “The study estimated it to be 6.4 days. But other statistical calculations ... showed that the incubation period could be as long as 14.22 days.” What's wrong here?



















 , where r is the radius of the Earth, and h is the observer's height above the Earth's surface. (This can be proved using the Pythagorean theorem.) Show that the units of this expression make sense.
, where r is the radius of the Earth, and h is the observer's height above the Earth's surface. (This can be proved using the Pythagorean theorem.) Show that the units of this expression make sense.