You are viewing the html version of Newtonian Physics, by Benjamin Crowell. This version is only designed for casual browsing, and may have some formatting problems.

(c) 1998-2006 Benjamin Crowell, licensed under the Creative Commons Attribution-ShareAlike license, or, at your option, the GFDL license. Photo credits are given at the end of the Adobe Acrobat version.

Contents
Section 5.1 - Newton's Third Law
Section 5.2 - Classification and Behavior of Forces
Section 5.3 - Analysis of Forces
Section 5.4 - Transmission of Forces by Low-Mass Objects
Section 5.5 - Objects Under Strain
Section 5.6 - Simple Machines: The Pulley
Section 5.7 - Summary

What forces act on the girl?

Chapter 5. Analysis of Forces

5.1 Newton's Third Law

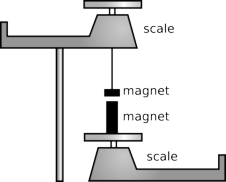
a / Two magnets exert forces on each other.

b / Two people's hands exert forces on each other.

c / Rockets work by pushing exhaust gases out the back. Newton's third law says that if the rocket exerts a backward force on the gases, the gases must make an equal forward force on the rocket. Rocket engines can function above the atmosphere, unlike propellers and jets, which work by pushing against the surrounding air.

d / A swimmer doing the breast stroke pushes backward against the water. By Newton's third law, the water pushes forward on her.

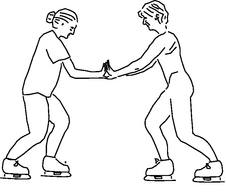
e / Newton's third law does not mean that forces always cancel out so that nothing can ever move. If these two figure skaters, initially at rest, push against each other, they will both move.

Newton created the modern concept of force starting from his insight that all the effects that govern motion are interactions between two objects: unlike the Aristotelian theory, Newtonian physics has no phenomena in which an object changes its own motion.

Is one object always the “order-giver” and the other the “order-follower”? As an example, consider a batter hitting a baseball. The bat definitely exerts a large force on the ball, because the ball accelerates drastically. But if you have ever hit a baseball, you also know that the ball makes a force on the bat --- often with painful results if your technique is as bad as mine!

How does the ball's force on the bat compare with the bat's force on the ball? The bat's acceleration is not as spectacular as the ball's, but maybe we shouldn't expect it to be, since the bat's mass is much greater. In fact, careful measurements of both objects' masses and accelerations would show that mballaball is very nearly equal to -mbatabat, which suggests that the ball's force on the bat is of the same magnitude as the bat's force on the ball, but in the opposite direction.

Figures a and b show two somewhat more practical laboratory experiments for investigating this issue accurately and without too much interference from extraneous forces.

In experiment a, a large magnet and a small magnet are weighed separately, and then one magnet is hung from the pan of the top balance so that it is directly above the other magnet. There is an attraction between the two magnets, causing the reading on the top scale to increase and the reading on the bottom scale to decrease. The large magnet is more “powerful” in the sense that it can pick up a heavier paperclip from the same distance, so many people have a strong expectation that one scale's reading will change by a far different amount than the other. Instead, we find that the two changes are equal in magnitude but opposite in direction: the force of the bottom magnet pulling down on the top one has the same strength as the force of the top one pulling up on the bottom one.

In experiment b, two people pull on two spring scales. Regardless of who tries to pull harder, the two forces as measured on the spring scales are equal. Interposing the two spring scales is necessary in order to measure the forces, but the outcome is not some artificial result of the scales' interactions with each other. If one person slaps another hard on the hand, the slapper's hand hurts just as much as the slappee's, and it doesn't matter if the recipient of the slap tries to be inactive. (Punching someone in the mouth causes just as much force on the fist as on the lips. It's just that the lips are more delicate. The forces are equal, but not the levels of pain and injury.)

Newton, after observing a series of results such as these, decided that there must be a fundamental law of nature at work:

Newton's third law

Forces occur in equal and opposite pairs: whenever object A exerts a force on object B, object B must also be exerting a force on object A. The two forces are equal in magnitude and opposite in direction.

In one-dimensional situations, we can use plus and minus signs to indicate the directions of forces, and Newton's third law can be written succinctly as $F_{\text{A on B}}=-F_{\text{B on A}}$ .

self-check: Figure d analyzes swimming using Newton's third law. Do a similar analysis for a sprinter leaving the starting line. (answer in the back of the PDF version of the book)

There is no cause and effect relationship between the two forces in Newton's third law. There is no “original” force, and neither one is a response to the other. The pair of forces is a relationship, like marriage, not a back-and-forth process like a tennis match. Newton came up with the third law as a generalization about all the types of forces with which he was familiar, such as frictional and gravitational forces. When later physicists discovered a new type force, such as the force that holds atomic nuclei together, they had to check whether it obeyed Newton's third law. So far, no violation of the third law has ever been discovered, whereas the first and second laws were shown to have limitations by Einstein and the pioneers of atomic physics.

The English vocabulary for describing forces is unfortunately rooted in Aristotelianism, and often implies incorrectly that forces are one-way relationships. It is unfortunate that a half-truth such as “the table exerts an upward force on the book” is so easily expressed, while a more complete and correct description ends up sounding awkward or strange: “the table and the book interact via a force,” or “the table and book participate in a force.”

To students, it often sounds as though Newton's third law implies nothing could ever change its motion, since the two equal and opposite forces would always cancel. The two forces, however, are always on two different objects, so it doesn't make sense to add them in the first place --- we only add forces that are acting on the same object. If two objects are interacting via a force and no other forces are involved, then both objects will accelerate --- in opposite directions!

f / It doesn't make sense for the man to talk about using the woman's money to cancel out his bar tab, because there is no good reason to combine his debts and her assets. Similarly, it doesn't make sense to refer to the equal and opposite forces of Newton's third law as canceling. It only makes sense to add up forces that are acting on the same object, whereas two forces related to each other by Newton's third law are always acting on two different objects.

A mnemonic for using Newton's third law correctly

Mnemonics are tricks for memorizing things. For instance, the musical notes that lie between the lines on the treble clef spell the word FACE, which is easy to remember. Many people use the mnemonic “SOHCAHTOA” to remember the definitions of the sine, cosine, and tangent in trigonometry. I have my own modest offering, POFOSTITO, which I hope will make it into the mnemonics hall of fame. It's a way to avoid some of the most common problems with applying Newton's third law correctly:

Example 1: A book lying on a table

◊ A book is lying on a table. What force is the Newton's-third-law partner of the earth's gravitational force on the book?

Answer: Newton's third law works like “B on A, A on B,” so the partner must be the book's gravitational force pulling upward on the planet earth. Yes, there is such a force! No, it does not cause the earth to do anything noticeable.

Incorrect answer: The table's upward force on the book is the Newton's-third-law partner of the earth's gravitational force on the book.

× This answer violates two out of three of the commandments of POFOSTITO. The forces are not of the same type, because the table's upward force on the book is not gravitational. Also, three objects are involved instead of two: the book, the table, and the planet earth.

Example 2: Pushing a box up a hill

◊ A person is pushing a box up a hill. What force is related by Newton's third law to the person's force on the box?

◊ The box's force on the person.

Incorrect answer: The person's force on the box is opposed by friction, and also by gravity.

× This answer fails all three parts of the POFOSTITO test, the most obvious of which is that three forces are referred to instead of a pair.

◊ Solved problem: More about example 2 — problem 20

◊ Solved problem: Why did it accelerate? — problem 18

Optional topic: Optional Topic: Newton's Third Law and Action at a Distance

Newton's third law is completely symmetric in the sense that neither force constitutes a delayed response to the other. Newton's third law does not even mention time, and the forces are supposed to agree at any given instant. This creates an interesting situation when it comes to noncontact forces. Suppose two people are holding magnets, and when one person waves or wiggles her magnet, the other person feels an effect on his. In this way they can send signals to each other from opposite sides of a wall, and if Newton's third law is correct, it would seem that the signals are transmitted instantly, with no time lag. The signals are indeed transmitted quite quickly, but experiments with electronically controlled magnets show that the signals do not leap the gap instantly: they travel at the same speed as light, which is an extremely high speed but not an infinite one.

Is this a contradiction to Newton's third law? Not really. According to current theories, there are no true noncontact forces. Action at a distance does not exist. Although it appears that the wiggling of one magnet affects the other with no need for anything to be in contact with anything, what really happens is that wiggling a magnet unleashes a shower of tiny particles called photons. The magnet shoves the photons out with a kick, and receives a kick in return, in strict obedience to Newton's third law. The photons fly out in all directions, and the ones that hit the other magnet then interact with it, again obeying Newton's third law.

Photons are nothing exotic, really. Light is made of photons, but our eyes receive such huge numbers of photons that we do not perceive them individually. The photons you would make by wiggling a magnet with your hand would be of a “color” that you cannot see, far off the red end of the rainbow. Book 6 in this series describes the evidence for the photon model of light.

Discussion Questions

◊ When you fire a gun, the exploding gases push outward in all directions, causing the bullet to accelerate down the barrel. What third-law pairs are involved? [Hint: Remember that the gases themselves are an object.]

◊ Tam Anh grabs Sarah by the hand and tries to pull her. She tries to remain standing without moving. A student analyzes the situation as follows. “If Tam Anh's force on Sarah is greater than her force on him, he can get her to move. Otherwise, she'll be able to stay where she is.” What's wrong with this analysis?

◊ You hit a tennis ball against a wall. Explain any and all incorrect ideas in the following description of the physics involved: “According to Newton's third law, there has to be a force opposite to your force on the ball. The opposite force is the ball's mass, which resists acceleration, and also air resistance.”

5.2 Classification and Behavior of Forces

g / A scientific classification system.

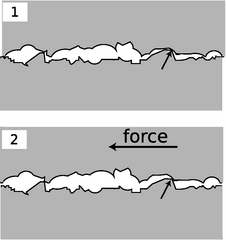
i / A model that correctly explains many properties of friction. The microscopic bumps and holes in two surfaces dig into each other, causing a frictional force.

j / Static friction: the tray doesn't slip on the waiter's fingers.

k / Kinetic friction: the car skids.

One of the most basic and important tasks of physics is to classify the forces of nature. I have already referred informally to “types” of forces such as friction, magnetism, gravitational forces, and so on. Classification systems are creations of the human mind, so there is always some degree of arbitrariness in them. For one thing, the level of detail that is appropriate for a classification system depends on what you're trying to find out. Some linguists, the “lumpers,” like to emphasize the similarities among languages, and a few extremists have even tried to find signs of similarities between words in languages as different as English and Chinese, lumping the world's languages into only a few large groups. Other linguists, the “splitters,” might be more interested in studying the differences in pronunciation between English speakers in New York and Connecticut. The splitters call the lumpers sloppy, but the lumpers say that science isn't worthwhile unless it can find broad, simple patterns within the seemingly complex universe.

Scientific classification systems are also usually compromises between practicality and naturalness. An example is the question of how to classify flowering plants. Most people think that biological classification is about discovering new species, naming them, and classifying them in the class-order-family-genus-species system according to guidelines set long ago. In reality, the whole system is in a constant state of flux and controversy. One very practical way of classifying flowering plants is according to whether their petals are separate or joined into a tube or cone --- the criterion is so clear that it can be applied to a plant seen from across the street. But here practicality conflicts with naturalness. For instance, the begonia has separate petals and the pumpkin has joined petals, but they are so similar in so many other ways that they are usually placed within the same order. Some taxonomists have come up with classification criteria that they claim correspond more naturally to the apparent relationships among plants, without having to make special exceptions, but these may be far less practical, requiring for instance the examination of pollen grains under an electron microscope.

In physics, there are two main systems of classification for forces. At this point in the course, you are going to learn one that is very practical and easy to use, and that splits the forces up into a relatively large number of types: seven very common ones that we'll discuss explicitly in this chapter, plus perhaps ten less important ones such as surface tension, which we will not bother with right now.

Professional physicists, however, are obsessed with finding simple patterns, so recognizing as many as fifteen or twenty types of forces strikes them as distasteful and overly complex. Since about the year 1900, physics has been on an aggressive program to discover ways in which these many seemingly different types of forces arise from a smaller number of fundamental ones. For instance, when you press your hands together, the force that keeps them from passing through each other may seem to have nothing to do with electricity, but at the atomic level, it actually does arise from electrical repulsion between atoms. By about 1950, all the forces of nature had been explained as arising from four fundamental types of forces at the atomic and nuclear level, and the lumping-together process didn't stop there. By the 1960's the length of the list had been reduced to three, and some theorists even believe that they may be able to reduce it to two or one. Although the unification of the forces of nature is one of the most beautiful and important achievements of physics, it makes much more sense to start this course with the more practical and easy system of classification. The unified system of four forces will be one of the highlights of the end of your introductory physics sequence.

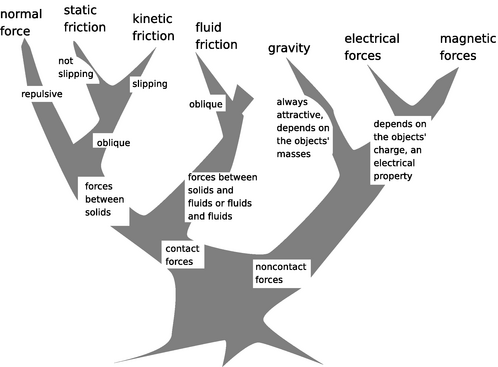
h / A practical classification scheme for forces.

The practical classification scheme which concerns us now can be laid out in the form of the tree shown in figure h. The most specific types of forces are shown at the tips of the branches, and it is these types of forces that are referred to in the POFOSTITO mnemonic. For example, electrical and magnetic forces belong to the same general group, but Newton's third law would never relate an electrical force to a magnetic force.

The broadest distinction is that between contact and noncontact forces, which has been discussed in the previous chapter. Among the contact forces, we distinguish between those that involve solids only and those that have to do with fluids, a term used in physics to include both gases and liquids. The terms “repulsive,” “attractive,” and “oblique” refer to the directions of the forces.

Repulsive forces are those that tend to push the two participating objects away from each other. More specifically, a repulsive contact force acts perpendicular to the surfaces at which the two objects touch, and a repulsive noncontact force acts along the line between the two objects.
Attractive forces pull the two objects toward one another, i.e., they act along the same line as repulsive forces, but in the opposite direction.
Oblique forces are those that act at some other angle.

It should not be necessary to memorize this diagram by rote. It is better to reinforce your memory of this system by calling to mind your commonsense knowledge of certain ordinary phenomena. For instance, we know that the gravitational attraction between us and the planet earth will act even if our feet momentarily leave the ground, and that although magnets have mass and are affected by gravity, most objects that have mass are nonmagnetic.

This diagram is meant to be as simple as possible while including most of the forces we deal with in everyday life. If you were an insect, you would be much more interested in the force of surface tension, which allowed you to walk on water. I have not included the nuclear forces, which are responsible for holding the nuclei of atoms, because they are not evident in everyday life.

You should not be afraid to invent your own names for types of forces that do not fit into the diagram. For instance, the force that holds a piece of tape to the wall has been left off of the tree, and if you were analyzing a situation involving scotch tape, you would be absolutely right to refer to it by some commonsense name such as “sticky force.”

On the other hand, if you are having trouble classifying a certain force, you should also consider whether it is a force at all. For instance, if someone asks you to classify the force that the earth has because of its rotation, you would have great difficulty creating a place for it on the diagram. That's because it's a type of motion, not a type of force!

While you were gradually increasing your force, the floor's frictional force on the fridge increased in response. The two forces on the fridge canceled, and the fridge didn't accelerate. How did the floor know how to respond with just the right amount of force? Figure i shows one possible model of friction that explains this behavior. (A scientific model is a description that we expect to be incomplete, approximate, or unrealistic in some ways, but that nevertheless succeeds in explaining a variety of phenomena.) Figure i/1 shows a microscopic view of the tiny bumps and holes in the surfaces of the floor and the refrigerator. The weight of the fridge presses the two surfaces together, and some of the bumps in one surface will settle as deeply as possible into some of the holes in the other surface. In i/2, your leftward force on the fridge has caused it to ride up a little higher on the bump in the floor labeled with a small arrow. Still more force is needed to get the fridge over the bump and allow it to start moving. Of course, this is occurring simultaneously at millions of places on the two surfaces.

Once you had gotten the fridge moving at constant speed, you found that you needed to exert less force on it. Since zero total force is needed to make an object move with constant velocity, the floor's rightward frictional force on the fridge has apparently decreased somewhat, making it easier for you to cancel it out. Our model also gives a plausible explanation for this fact: as the surfaces slide past each other, they don't have time to settle down and mesh with one another, so there is less friction.

Even though this model is intuitively appealing and fairly successful, it should not be taken too seriously, and in some situations it is misleading. For instance, fancy racing bikes these days are made with smooth tires that have no tread --- contrary to what we'd expect from our model, this does not cause any decrease in friction. Machinists know that two very smooth and clean metal surfaces may stick to each other firmly and be very difficult to slide apart. This cannot be explained in our model, but makes more sense in terms of a model in which friction is described as arising from chemical bonds between the atoms of the two surfaces at their points of contact: very flat surfaces allow more atoms to come in contact.

Since friction changes its behavior dramatically once the surfaces come unstuck, we define two separate types of frictional forces. Static friction is friction that occurs between surfaces that are not slipping over each other. Slipping surfaces experience kineticfriction. “Kinetic” means having to do with motion. The forces of static and kinetic friction, notated Fs and Fk, are always parallel to the surface of contact between the two objects.

self-check: 1. When a baseball player slides in to a base, is the friction static, or kinetic?

2. A mattress stays on the roof of a slowly accelerating car. Is the friction static or kinetic?

3. Does static friction create heat? Kinetic friction? (answer in the back of the PDF version of the book)

The maximum possible force of static friction depends on what kinds of surfaces they are, and also on how hard they are being pressed together. The approximate mathematical relationships can be expressed as follows:

Fs = -Fapplied , when |Fapplied| < μs|FN| ,

where μs is a unitless number, called the coefficient of static friction, which depends on what kinds of surfaces they are. The maximum force that static friction can supply, μs|FN|, represents the boundary between static and kinetic friction. It depends on the normal force, which is numerically equal to whatever force is pressing the two surfaces together. In terms of our model, if the two surfaces are being pressed together more firmly, a greater sideways force will be required in order to make the irregularities in the surfaces ride up and over each other.

Note that just because we use an adjective such as “applied” to refer to a force, that doesn't mean that there is some special type of force called the “applied force.” The applied force could be any type of force, or it could be the sum of more than one force trying to make an object move.

The force of kinetic friction on each of the two objects is in the direction that resists the slippage of the surfaces. Its magnitude is usually well approximated as

|Fk| = μk|FN|

where μk is the coefficient of kinetic friction. Kinetic friction is usually more or less independent of velocity.

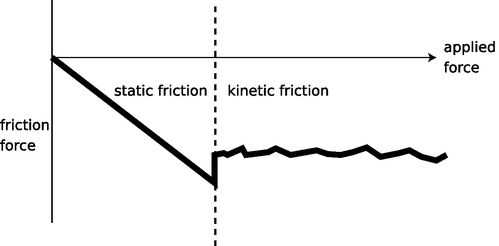
l / We choose a coordinate system in which the applied force, i.e., the force trying to move the objects, is positive. The friction force is then negative, since it is in the opposite direction. As you increase the applied force, the force of static friction increases to match it and cancel it out, until the maximum force of static friction is surpassed. The surfaces then begin slipping past each other, and the friction force becomes smaller in absolute value.

self-check: Can a frictionless surface exert a normal force? Can a frictional force exist without a normal force? (answer in the back of the PDF version of the book)

If you try to accelerate or decelerate your car too quickly, the forces between your wheels and the road become too great, and they begin slipping. This is not good, because kinetic friction is weaker than static friction, resulting in less control. Also, if this occurs while you are turning, the car's handling changes abruptly because the kinetic friction force is in a different direction than the static friction force had been: contrary to the car's direction of motion, rather than contrary to the forces applied to the tire.

Most people respond with disbelief when told of the experimental evidence that both static and kinetic friction are approximately independent of the amount of surface area in contact. Even after doing a hands-on exercise with spring scales to show that it is true, many students are unwilling to believe their own observations, and insist that bigger tires “give more traction.” In fact, the main reason why you would not want to put small tires on a big heavy car is that the tires would burst!

Although many people expect that friction would be proportional to surface area, such a proportionality would make predictions contrary to many everyday observations. A dog's feet, for example, have very little surface area in contact with the ground compared to a human's feet, and yet we know that a dog can often win a tug-of-war with a person.

The reason a smaller surface area does not lead to less friction is that the force between the two surfaces is more concentrated, causing their bumps and holes to dig into each other more deeply.

self-check: Find the direction of each of the forces in figure m. (answer in the back of the PDF version of the book)

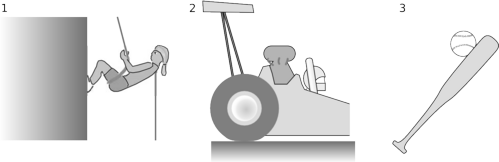
m / 1. The cliff's normal force on the climber's feet. 2. The track's static frictional force on the wheel of the accelerating dragster. 3. The ball's normal force on the bat.

Example 3: Locomotives

Looking at a picture of a locomotive, n, we notice two obvious things that are different from an automobile. Where a car typically has two drive wheels, a locomotive normally has many --- ten in this example. (Some also have smaller, unpowered wheels in front of and behind the drive wheels, but this example doesn't.) Also, cars these days are generally built to be as light as possible for their size, whereas locomotives are very massive, and no effort seems to be made to keep their weight low. (The steam locomotive in the photo is from about 1900, but this is true even for modern diesel and electric trains.)

n / Example 3.

The reason locomotives are built to be so heavy is for traction. The upward normal force of the rails on the wheels, FN, cancels the downward force of gravity, FW, so ignoring plus and minus signs, these two forces are equal in absolute value, FN=FW. Given this amount of normal force, the maximum force of static friction is Fs=μs FN=μs FW. This static frictional force, of the rails pushing forward on the wheels, is the only force that can accelerate the train, pull it uphill, or cancel out the force of air resistance while cruising at constant speed. The coefficient of static friction for steel on steel is about 1/4, so no locomotive can pull with a force greater than about 1/4 of its own weight. If the engine is capable of supplying more than that amount of force, the result will be simply to break static friction and spin the wheels.

The reason this is all so different from the situation with a car is that a car isn't pulling something else. If you put extra weight in a car, you improve the traction, but you also increase the inertia of the car, and make it just as hard to accelerate. In a train, the inertia is almost all in the cars being pulled, not in the locomotive.

The other fact we have to explain is the large number of driving wheels. First, we have to realize that increasing the number of driving wheels neither increases nor decreases the total amount of static friction, because static friction is independent of the amount of surface area in contact. (The reason four-wheel-drive is good in a car is that if one or more of the wheels is slipping on ice or in mud, the other wheels will still have traction. This isn't typically an issue for a train, since all the wheels experience the same conditions.) The advantage of having more driving wheels on a train is that it allows us to increase the weight of the train without crushing the rails, or damaging bridges.

Fluid friction

Try to drive a nail into a waterfall and you will be confronted with the main difference between solid friction and fluid friction. Fluid friction is purely kinetic; there is no static fluid friction. The nail in the waterfall may tend to get dragged along by the water flowing past it, but it does not stick in the water. The same is true for gases such as air: recall that we are using the word “fluid” to include both gases and liquids.

Unlike solid kinetic friction, the force of fluid friction increases rapidly with velocity. In many cases, the force is approximately proportional to the square of the velocity,

$F_{\text{fluid friction}} \propto c\rho Av^2 ,$

where A is the cross-sectional area of the object, ρ is the density of the fluid, and c is a constant of proportionality that depends partly on the type of fluid and partly on how streamlined the object is.

Discussion Questions

◊ A student states that when he tries to push his refrigerator, the reason it won't move is because Newton's third law says there's an equal and opposite frictional force pushing back. After all, the static friction force is equal and opposite to the applied force. How would you convince him he is wrong?

◊ Kinetic friction is usually more or less independent of velocity. However, inexperienced drivers tend to produce a jerk at the last moment of deceleration when they stop at a stop light. What does this tell you about the kinetic friction between the brake shoes and the brake drums?

◊ Some of the following are correct descriptions of types of forces that could be added on as new branches of the classification tree. Others are not really types of forces, and still others are not force phenomena at all. In each case, decide what's going on, and if appropriate, figure out how you would incorporate them into the tree.

sticky force	makes tape stick to things
opposite force	the force that Newton’s third law says relates to every force you make
flowing force	the force that water carries with it as it flows out of a hose
surface tension	lets insects walk on water
horizontal force	a force that is horizontal
motor force	the force that a motor makes on the thing it is turning
canceled force	a force that is being canceled out by some other force

5.3 Analysis of Forces

Discussion question C.

Newton's first and second laws deal with the total of all the forces exerted on a specific object, so it is very important to be able to figure out what forces there are. Once you have focused your attention on one object and listed the forces on it, it is also helpful to describe all the corresponding forces that must exist according to Newton's third law. We refer to this as “analyzing the forces” in which the object participates.

Example 4: A barge

A barge is being pulled along a canal by teams of horses on the shores. Analyze all the forces in which the barge participates.


force acting on barge	force related to it by Newton’s third law

ropes’ forward normal forces on barge	barge’s backward normal force on ropes

water’s backward fluid friction force on barge	barge’s forward fluid friction force on water

planet earth’s downward gravitational force on barge	barge’s upward gravitational force on earth

water’s upward “floating” force on barge	barge’s downward “floating” force on water

Here I've used the word “floating” force as an example of a sensible invented term for a type of force not classified on the tree in the previous section. A more formal technical term would be “hydrostatic force.”

Note how the pairs of forces are all structured as “A's force on B, B's force on A”: ropes on barge and barge on ropes; water on barge and barge on water. Because all the forces in the left column are forces acting on the barge, all the forces in the right column are forces being exerted by the barge, which is why each entry in the column begins with “barge.”

Often you may be unsure whether you have forgotten one of the forces. Here are three strategies for checking your list:

See what physical result would come from the forces you've found so far. Suppose, for instance, that you'd forgotten the “floating” force on the barge in the example above. Looking at the forces you'd found, you would have found that there was a downward gravitational force on the barge which was not canceled by any upward force. The barge isn't supposed to sink, so you know you need to find a fourth, upward force.

Another technique for finding missing forces is simply to go through the list of all the common types of forces and see if any of them apply.

Make a drawing of the object, and draw a dashed boundary line around it that separates it from its environment. Look for points on the boundary where other objects come in contact with your object. This strategy guarantees that you'll find every contact force that acts on the object, although it won't help you to find non-contact forces.

The following is another example in which we can profit by checking against our physical intuition for what should be happening.

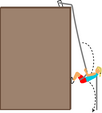
Example 5: Rappelling

As shown in the figure below, Cindy is rappelling down a cliff. Her downward motion is at constant speed, and she takes little hops off of the cliff, as shown by the dashed line. Analyze the forces in which she participates at a moment when her feet are on the cliff and she is pushing off.


force acting on Cindy	force related to it by Newton’s third law

planet earth’s downward gravitational force on Cindy	Cindy’s upward gravitational force on earth

ropes upward frictional force on Cindy (her hand)	Cindy’s downward frictional force on the rope

cliff’s rightward normal force on Cindy	Cindy’s leftward normal force on the cliff

The two vertical forces cancel, which is what they should be doing if she is to go down at a constant rate. The only horizontal force on her is the cliff's force, which is not canceled by any other force, and which therefore will produce an acceleration of Cindy to the right. This makes sense, since she is hopping off. (This solution is a little oversimplified, because the rope is slanting, so it also applies a small leftward force to Cindy. As she flies out to the right, the slant of the rope will increase, pulling her back in more strongly.)

I believe that constructing the type of table described in this section is the best method for beginning students. Most textbooks, however, prescribe a pictorial way of showing all the forces acting on an object. Such a picture is called a free-body diagram. It should not be a big problem if a future physics professor expects you to be able to draw such diagrams, because the conceptual reasoning is the same. You simply draw a picture of the object, with arrows representing the forces that are acting on it. Arrows representing contact forces are drawn from the point of contact, noncontact forces from the center of mass. Free-body diagrams do not show the equal and opposite forces exerted by the object itself.

Discussion Questions

◊ In the example of the barge going down the canal, I referred to a “floating” or “hydrostatic” force that keeps the boat from sinking. If you were adding a new branch on the force-classification tree to represent this force, where would it go?

◊ A pool ball is rebounding from the side of the pool table. Analyze the forces in which the ball participates during the short time when it is in contact with the side of the table.

◊ The earth's gravitational force on you, i.e., your weight, is always equal to mg, where m is your mass. So why can you get a shovel to go deeper into the ground by jumping onto it? Just because you're jumping, that doesn't mean your mass or weight is any greater, does it?

5.4 Transmission of Forces by Low-Mass Objects

p / The Golden Gate Bridge's roadway is held up by the tension in the vertical cables.

You're walking your dog. The dog wants to go faster than you do, and the leash is taut. Does Newton's third law guarantee that your force on your end of the leash is equal and opposite to the dog's force on its end? If they're not exactly equal, is there any reason why they should be approximately equal?

If there was no leash between you, and you were in direct contact with the dog, then Newton's third law would apply, but Newton's third law cannot relate your force on the leash to the dog's force on the leash, because that would involve three separate objects. Newton's third law only says that your force on the leash is equal and opposite to the leash's force on you,

FyL = - FLy ,

and that the dog's force on the leash is equal and opposite to its force on the dog

FdL = - FLd .

Still, we have a strong intuitive expectation that whatever force we make on our end of the leash is transmitted to the dog, and vice-versa. We can analyze the situation by concentrating on the forces that act on the leash, FdL and FyL. According to Newton's second law, these relate to the leash's mass and acceleration:

FdL + FyL = mLaL .

The leash is far less massive then any of the other objects involved, and if mL is very small, then apparently the total force on the leash is also very small, FdL + FyL≈ 0, and therefore

FdL≈ - FyL .

Thus even though Newton's third law does not apply directly to these two forces, we can approximate the low-mass leash as if it was not intervening between you and the dog. It's at least approximately as if you and the dog were acting directly on each other, in which case Newton's third law would have applied.

In general, low-mass objects can be treated approximately as if they simply transmitted forces from one object to another. This can be true for strings, ropes, and cords, and also for rigid objects such as rods and sticks.

o / If we imagine dividing a taut rope up into small segments, then any segment has forces pulling outward on it at each end. If the rope is of negligible mass, then all the forces equal +T or -T, where T, the tension, is a single number.

If you look at a piece of string under a magnifying glass as you pull on the ends more and more strongly, you will see the fibers straightening and becoming taut. Different parts of the string are apparently exerting forces on each other. For instance, if we think of the two halves of the string as two objects, then each half is exerting a force on the other half. If we imagine the string as consisting of many small parts, then each segment is transmitting a force to the next segment, and if the string has very little mass, then all the forces are equal in magnitude. We refer to the magnitude of the forces as the tension in the string, T. Although the tension is measured in units of Newtons, it is not itself a force. There are many forces within the string, some in one direction and some in the other direction, and their magnitudes are only approximately equal. The concept of tension only makes sense as a general, approximate statement of how big all the forces are.

If a rope goes over a pulley or around some other object, then the tension throughout the rope is approximately equal so long as there is not too much friction. A rod or stick can be treated in much the same way as a string, but it is possible to have either compression or tension.

Since tension is not a type of force, the force exerted by a rope on some other object must be of some definite type such as static friction, kinetic friction, or a normal force. If you hold your dog's leash with your hand through the loop, then the force exerted by the leash on your hand is a normal force: it is the force that keeps the leash from occupying the same space as your hand. If you grasp a plain end of a rope, then the force between the rope and your hand is a frictional force.

A more complex example of transmission of forces is the way a car accelerates. Many people would describe the car's engine as making the force that accelerates the car, but the engine is part of the car, so that's impossible: objects can't make forces on themselves. What really happens is that the engine's force is transmitted through the transmission to the axles, then through the tires to the road. By Newton's third law, there will thus be a forward force from the road on the tires, which accelerates the car.

Discussion Question

◊ When you step on the gas pedal, is your foot's force being transmitted in the sense of the word used in this section?

5.5 Objects Under Strain

A string lengthens slightly when you stretch it. Similarly, we have already discussed how an apparently rigid object such as a wall is actually flexing when it participates in a normal force. In other cases, the effect is more obvious. A spring or a rubber band visibly elongates when stretched.

Common to all these examples is a change in shape of some kind: lengthening, bending, compressing, etc. The change in shape can be measured by picking some part of the object and measuring its position, x. For concreteness, let's imagine a spring with one end attached to a wall. When no force is exerted, the unfixed end of the spring is at some position xo. If a force acts at the unfixed end, its position will change to some new value of x. The more force, the greater the departure of x from xo.

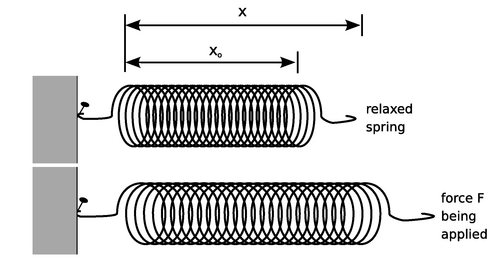
q / Defining the quantities F, x, and xo in Hooke's law.

Back in Newton's time, experiments like this were considered cutting-edge research, and his contemporary Hooke is remembered today for doing them and for coming up with a simple mathematical generalization called Hooke's law:

$F \approx k(x-x_o) . \shoveright{\text{[force required to stretch a spring; valid}}$

$\text{for small forces only]}$

Here k is a constant, called the spring constant, that depends on how stiff the object is. If too much force is applied, the spring exhibits more complicated behavior, so the equation is only a good approximation if the force is sufficiently small. Usually when the force is so large that Hooke's law is a bad approximation, the force ends up permanently bending or breaking the spring.

Although Hooke's law may seem like a piece of trivia about springs, it is actually far more important than that, because all solid objects exert Hooke's-law behavior over some range of sufficiently small forces. For example, if you push down on the hood of a car, it dips by an amount that is directly proportional to the force. (But the car's behavior would not be as mathematically simple if you dropped a boulder on the hood!)

◊ Solved problem: Combining springs — problem 14

◊ Solved problem: Young's modulus — problem 16

Discussion Question

◊ A car is connected to its axles through big, stiff springs called shock absorbers, or “shocks.” Although we've discussed Hooke's law above only in the case of stretching a spring, a car's shocks are continually going through both stretching and compression. In this situation, how would you interpret the positive and negative signs in Hooke's law?

5.6 Simple Machines: The Pulley

Even the most complex machines, such as cars or pianos, are built out of certain basic units called simple machines. The following are some of the main functions of simple machines:

transmitting a force: The chain on a bicycle transmits a force from the crank set to the rear wheel.

changing the direction of a force: If you push down on a seesaw, the other end goes up.

changing the speed and precision of motion: When you make the “come here” motion, your biceps only moves a couple of centimeters where it attaches to your forearm, but your arm moves much farther and more rapidly.

changing the amount of force: A lever or pulley can be used to increase or decrease the amount of force.

You are now prepared to understand one-dimensional simple machines, of which the pulley is the main example.

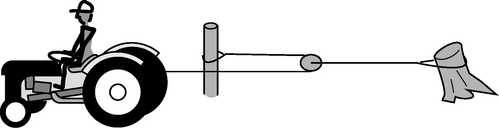
r / Example 6.

Example 6: A pulley

◊ Farmer Bill says this pulley arrangement doubles the force of his tractor. Is he just a dumb hayseed, or does he know what he's doing?

◊ To use Newton's first law, we need to pick an object and consider the sum of the forces on it. Since our goal is to relate the tension in the part of the cable attached to the stump to the tension in the part attached to the tractor, we should pick an object to which both those cables are attached, i.e., the pulley itself. As discussed in section 5.4, the tension in a string or cable remains approximately constant as it passes around a pulley, provided that there is not too much friction. There are therefore two leftward forces acting on the pulley, each equal to the force exerted by the tractor. Since the acceleration of the pulley is essentially zero, the forces on it must be canceling out, so the rightward force of the pulley-stump cable on the pulley must be double the force exerted by the tractor. Yes, Farmer Bill knows what he's talking about.

Summary

Vocabulary

repulsive — describes a force that tends to push the two participating objects apart

attractive — describes a force that tends to pull the two participating objects together

oblique — describes a force that acts at some other angle, one that is not a direct repulsion or attraction

normal force — the force that keeps two objects from occupying the same space

static friction — a friction force between surfaces that are not slipping past each other

kinetic friction — a friction force between surfaces that are slipping past each other

fluid — a gas or a liquid

fluid friction — a friction force in which at least one of the object is is a fluid

spring constant — the constant of proportionality between force and elongation of a spring or other object under strain

Notation

FN — a normal force

Fs — a static frictional force

Fk — a kinetic frictional force

μs — the coefficient of static friction; the constant of proportionality between the maximum static frictional force and the normal force; depends on what types of surfaces are involved

μk — the coefficient of kinetic friction; the constant of proportionality between the kinetic frictional force and the normal force; depends on what types of surfaces are involved

k — the spring constant; the constant of proportionality between the force exerted on an object and the amount by which the object is lengthened or compressed

Summary

Newton's third law states that forces occur in equal and opposite pairs. If object A exerts a force on object B, then object B must simultaneously be exerting an equal and opposite force on object A. Each instance of Newton's third law involves exactly two objects, and exactly two forces, which are of the same type.

There are two systems for classifying forces. We are presently using the more practical but less fundamental one. In this system, forces are classified by whether they are repulsive, attractive, or oblique; whether they are contact or noncontact forces; and whether the two objects involved are solids or fluids.

Static friction adjusts itself to match the force that is trying to make the surfaces slide past each other, until the maximum value is reached,

|Fs|<μs|FN| .

Once this force is exceeded, the surfaces slip past one another, and kinetic friction applies,

|Fk| = μk|FN| .

Both types of frictional force are nearly independent of surface area, and kinetic friction is usually approximately independent of the speed at which the surfaces are slipping.

A good first step in applying Newton's laws of motion to any physical situation is to pick an object of interest, and then to list all the forces acting on that object. We classify each force by its type, and find its Newton's-third-law partner, which is exerted by the object on some other object.

When two objects are connected by a third low-mass object, their forces are transmitted to each other nearly unchanged.

Objects under strain always obey Hooke's law to a good approximation, as long as the force is small. Hooke's law states that the stretching or compression of the object is proportional to the force exerted on it,

F ≈ k(x-xo) .

Homework Problems

s / Problem 6.

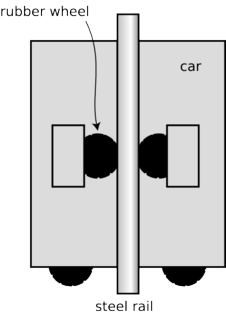
t / Problem 9.

u / Problem 10.

v / Problem 13.

w / Problem 14.

x / Problem 17.

y / Problem 19.

1. A little old lady and a pro football player collide head-on. Compare their forces on each other, and compare their accelerations. Explain.

2. The earth is attracted to an object with a force equal and opposite to the force of the earth on the object. If this is true, why is it that when you drop an object, the earth does not have an acceleration equal and opposite to that of the object?

3. When you stand still, there are two forces acting on you, the force of gravity (your weight) and the normal force of the floor pushing up on your feet. Are these forces equal and opposite? Does Newton's third law relate them to each other? Explain.

In problems 4-8, analyze the forces using a table in the format shown in section 5.3. Analyze the forces in which the italicized object participates.

4. A magnet is stuck underneath a parked car. (See instructions above.)

5. Analyze two examples of objects at rest relative to the earth that are being kept from falling by forces other than the normal force. Do not use objects in outer space, and do not duplicate problem 4 or 8. (See instructions above.)

6. A person is rowing a boat, with her feet braced. She is doing the part of the stroke that propels the boat, with the ends of the oars in the water (not the part where the oars are out of the water). (See instructions above.)

7. A farmer is in a stall with a cow when the cow decides to press him against the wall, pinning him with his feet off the ground. Analyze the forces in which the farmer participates. (See instructions above.)

8. A propeller plane is cruising east at constant speed and altitude. (See instructions above.)

9. Today's tallest buildings are really not that much taller than the tallest buildings of the 1940s. One big problem with making an even taller skyscraper is that every elevator needs its own shaft running the whole height of the building. So many elevators are needed to serve the building's thousands of occupants that the elevator shafts start taking up too much of the space within the building. An alternative is to have elevators that can move both horizontally and vertically: with such a design, many elevator cars can share a few shafts, and they don't get in each other's way too much because they can detour around each other. In this design, it becomes impossible to hang the cars from cables, so they would instead have to ride on rails which they grab onto with wheels. Friction would keep them from slipping. The figure shows such a frictional elevator in its vertical travel mode. (The wheels on the bottom are for when it needs to switch to horizontal motion.)
(a) If the coefficient of static friction between rubber and steel is μs, and the maximum mass of the car plus its passengers is M, how much force must there be pressing each wheel against the rail in order to keep the car from slipping? (Assume the car is not accelerating.)(answer check available at lightandmatter.com)
(b) Show that your result has physically reasonable behavior with respect to μs. In other words, if there was less friction, would the wheels need to be pressed more firmly or less firmly? Does your equation behave that way?

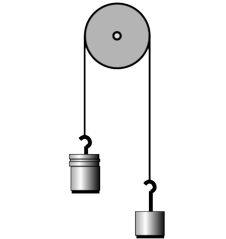
10. Unequal masses M and m are suspended from a pulley as shown in the figure.
(a) Analyze the forces in which mass m participates, using a table the format shown in section 5.3. [The forces in which the other mass participates will of course be similar, but not numerically the same.]
(b) Find the magnitude of the accelerations of the two masses. [Hints: (1) Pick a coordinate system, and use positive and negative signs consistently to indicate the directions of the forces and accelerations. (2) The two accelerations of the two masses have to be equal in magnitude but of opposite signs, since one side eats up rope at the same rate at which the other side pays it out. (3) You need to apply Newton's second law twice, once to each mass, and then solve the two equations for the unknowns: the acceleration, a, and the tension in the rope, T.]
(c) Many people expect that in the special case of M=m, the two masses will naturally settle down to an equilibrium position side by side. Based on your answer from part b, is this correct?
(d) Find the tension in the rope, T.
(e) Interpret your equation from part d in the special case where one of the masses is zero. Here “interpret” means to figure out what happens mathematically, figure out what should happen physically, and connect the two.

11. A tugboat of mass m pulls a ship of mass M, accelerating it. The speeds are low enough that you can ignore fluid friction acting on their hulls, although there will of course need to be fluid friction acting on the tug's propellers.
(a) Analyze the forces in which the tugboat participates, using a table in the format shown in section 5.3. Don't worry about vertical forces.
(b) Do the same for the ship.
(c) Assume now that water friction on the two vessels' hulls is negligible. If the force acting on the tug's propeller is F, what is the tension, T, in the cable connecting the two ships? [Hint: Write down two equations, one for Newton's second law applied to each object. Solve these for the two unknowns T and a.](answer check available at lightandmatter.com)
(d) Interpret your answer in the special cases of M=0 and M=∞.

12. Explain why it wouldn't make sense to have kinetic friction be stronger than static friction.

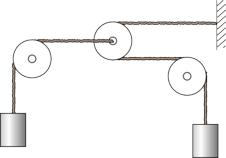
13. In the system shown in the figure, the pulleys on the left and right are fixed, but the pulley in the center can move to the left or right. The two masses are identical. Show that the mass on the left will have an upward acceleration equal to g/5. Assume all the ropes and pulleys are massless and rictionless.

14. The figure shows two different ways of combining a pair of identical springs, each with spring constant k. We refer to the top setup as parallel, and the bottom one as a series arrangement.
(a) For the parallel arrangement, analyze the forces acting on the connector piece on the left, and then use this analysis to determine the equivalent spring constant of the whole setup. Explain whether the combined spring constant should be interpreted as being stiffer or less stiff.
(b) For the series arrangement, analyze the forces acting on each spring and figure out the same things.(solution in the pdf version of the book)

15. Generalize the results of problem 14 to the case where the two spring constants are unequal.

16. (a) Using the solution of problem 14, which is given in the back of the book, predict how the spring constant of a fiber will depend on its length and cross-sectional area.
(b) The constant of proportionality is called the Young's modulus, E, and typical values of the Young's modulus are about 1010 to 1011. What units would the Young's modulus have in the SI (meter-kilogram-second) system? (solution in the pdf version of the book)

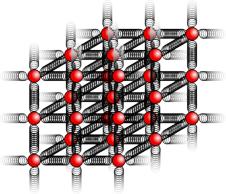
17. This problem depends on the results of problems 14 and 16, whose solutions are in the back of the book When atoms form chemical bonds, it makes sense to talk about the spring constant of the bond as a measure of how “stiff” it is. Of course, there aren't really little springs --- this is just a mechanical model. The purpose of this problem is to estimate the spring constant, k, for a single bond in a typical piece of solid matter. Suppose we have a fiber, like a hair or a piece of fishing line, and imagine for simplicity that it is made of atoms of a single element stacked in a cubical manner, as shown in the figure, with a center-to-center spacing b. A typical value for b would be about 10-10 m.
(a) Find an equation for k in terms of b, and in terms of the Young's modulus, E, defined in problem 16 and its solution.
(b) Estimate k using the numerical data given in problem 16.
(c) Suppose you could grab one of the atoms in a diatomic molecule like H2 or O2, and let the other atom hang vertically below it. Does the bond stretch by any appreciable fraction due to gravity?

18. (solution in the pdf version of the book) In each case, identify the force that causes the acceleration, and give its Newton's-third-law partner. Describe the effect of the partner force. (a) A swimmer speeds up. (b) A golfer hits the ball off of the tee. (c) An archer fires an arrow. (d) A locomotive slows down.

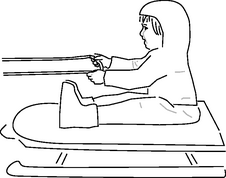
19. Ginny has a plan. She is going to ride her sled while her dog Foo pulls her. However, Ginny hasn't taken physics, so there may be a problem: she may slide right off the sled when Foo starts pulling.
(a) Analyze all the forces in which Ginny participates, making a table as in section 5.3.
(b) Analyze all the forces in which the sled participates.
(c) The sled has mass m, and Ginny has mass M. The coefficient of static friction between the sled and the snow is μ1, and μ2 is the corresponding quantity for static friction between the sled and her snow pants. Ginny must have a certain minimum mass so that she will not slip off the sled. Find this in terms of the other three variables.(answer check available at lightandmatter.com)
(d) Interpreting your equation from part c, under what conditions will there be no physically realistic solution for M? Discuss what this means physically.

20. (solution in the pdf version of the book) Example 2 on page 144 involves a person pushing a box up a hill. The incorrect answer describes three forces. For each of these three forces, give the force that it is related to by Newton's third law, and state the type of force.

21. Example 6 on page 160 describes a force-doubling setup involving a pulley. Make up a more complicated arrangement, using more than one pulley, that would multiply the force by a factor greater than two.

22. Pick up a heavy object such as a backpack or a chair, and stand on a bathroom scale. Shake the object up and down. What do you observe? Interpret your observations in terms of Newton's third law.

23. A cop investigating the scene of an accident measures the length L of a car's skid marks in order to find out its speed v at the beginning of the skid. Express v in terms of L and any other relevant variables.(answer check available at lightandmatter.com)

24. The following reasoning leads to an apparent paradox; explain what's wrong with the logic. A baseball player hits a ball. The ball and the bat spend a fraction of a second in contact. During that time they're moving together, so their accelerations must be equal. Newton's third law says that their forces on each other are also equal. But a=F/m, so how can this be, since their masses are unequal? (Note that the paradox isn't resolved by considering the force of the batter's hands on the bat. Not only is this force very small compared to the ball-bat force, but the batter could have just thrown the bat at the ball.)

25. Driving down a hill inclined at an angle θ with respect to horizontal, you slam on the brakes to keep from hitting a deer.
(a) Analyze the forces. (Ignore rolling resistance and air friction.)
(b) Find the car's maximum possible deceleration, a (expressed as a positive number), in terms of g, θ, and the relevant coefficient of friction.(answer check available at lightandmatter.com)
(c) Explain physically why the car's mass has no effect on your answer.
(d) Discuss the mathematical behavior and physical interpretation of your result for negative values of θ.
(e) Do the same for very large positive values of θ.

26. (solution in the pdf version of the book) (a) Compare the mass of a one-liter water bottle on earth, on the moon, and in interstellar space.
(b) Do the same for its weight.

27. An ice skater builds up some speed, and then coasts across the ice passively in a straight line. (a) Analyze the forces. (b) If his initial speed is v, and the coefficient of kinetic friction is μk, find the maximum theoretical distance he can glide before coming to a stop. Ignore air resistance. (c) Show that your answer to part b has the right units. (d) Show that your answer to part b depends on the variables in a way that makes sense physically. (d) Evaluate your answer numerically for μk=0.0046, and a world-record speed of 14.58 m/s. (The coefficient of friction was measured by De Koning et al., using special skates worn by real speed skaters.) (e) Comment on whether your answer in part d seems realistic. If it doesn't, suggest possible reasons why.

Dynamics

Newton's third law

Optional topic: Optional Topic: Newton's Third Law and Action at a Distance

Discussion Questions

Example 3: Locomotives

Example 4: A barge

Example 5: Rappelling

Discussion Questions

Discussion Question

Discussion Question

Example 6: A pulley