|
Welcome to the Classic Problems Page!Here you will find a selection of marvelous little problems I have collected over the years
that will test your mathematical mettle. If you're looking for a challenge, or something to
work your mind a bit more, give one of these little puzzles a shot. |
Solve the equation 4x + 6x = 9x manually.
Take any pair of consecutive odd integers. Add their reciprocals.
After simplifying the resulting fraction, prove the numerator and denominator will be two sides of a right triangle.
Show that for any real number x, the number (x2 + 34x - 71)(x2 + 2x - 7)-1 can not be between 5 and 9.
John went to the bank to cash a check for a sum under $100. The cashier confused the cents with the dollars (for example, if the check was for $19.45, John was given $45.19). John got the money and, after spending $3.50, realized he had exactly twice the amount written on the check.
How much was the check for?
Show that if n is a positive integer such that (2n + 1) is a perfect square, then (n + 1) is the sum of two successive perfect squares.
If a, b, and c are the lengths of three segments that can form a triangle, show algebraically and geometrically that the three lengths
1/(a+b), 1/(a+c) and 1/(b+c) can form a triangle also.
Square ABCD has side length 2. A line drawn from C is tangent to a semicircle with diameter AD and intersects AB at point E.
Find the exact value of CE.
| In the image at right, each of the three circles is tangent to the other two, and to the line. How are the radii of the three circles related? | 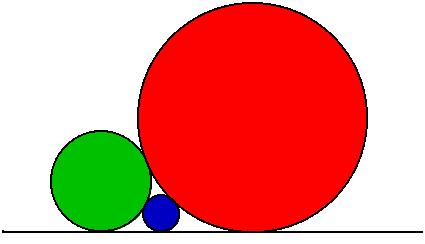 |
Looking down an alley, you observe two ladders laying up against opposite walls. From where you're standing, they appear to cross. The point at which they appear to cross is 8 feet above the ground. One ladder is 20 feet long, the other is 30 feet long. How wide is the alley?
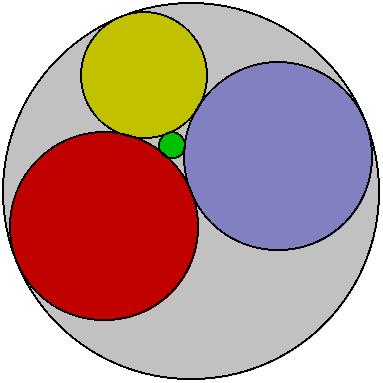
In the diagram below, the red and blue circles both have a radius that is one half of the larger, gray circle. That is, if the radius of the large circle is r, the radii of the red and blue circles are each r / 2. Assuming that the red, blue, and yellow circles are all tangent to the gray circle, and the green circle is tangent to the red, blue and yellow circles, find the radii of the yellow and green circles, in terms of r.
Draw an acute scalene triangle ABC. Contruct medians AD and BE. Create segment BF so E is its midpoint, and create segment AG so D is its midpoint. Prove that C is the midpoint of segment GF.
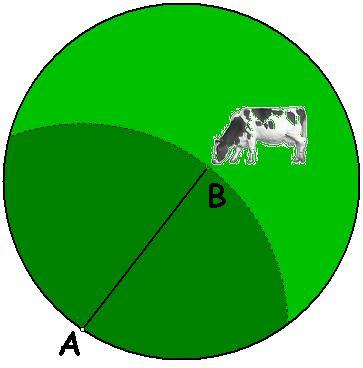
In the figure above, the cow is allowed to graze within a fenced, circular field. Her leash, AB, is fastened to a point on the perimeter of the circle, A. She is attached to the other end, B. Find the length of AB in terms of the radius of the circular field, R, and at most one other variable, if the area she is allowed to graze (darker green area) is to be exactly one-half of the area of the circular field.
In isosceles triangle ABC with AB = AC and angle A measuring 20 degrees, draw angles CBD and BCE so that angle CBD is 60 degrees and angle BCE is 50 degrees. Find angle EDB.
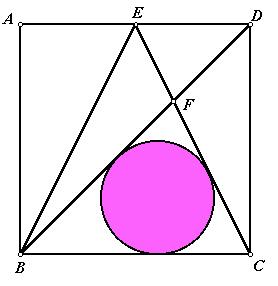 |
In the image at left, ABCD is a square. E is the midpoint of AD, and the purple circle is inscribed in triangle FBC. If the square has side length s, what is the radius of the circle, in terms of s ? Leave your answer in radical form...no decimals. |
| In the diagram at right, the large triangle is a right triangle. The blue quadrilaterals are all squares. The three circles are inscribed inside their three respective triangles. Show that the radius of the red circle is the geometric mean between the radii of the green and yellow circles. | 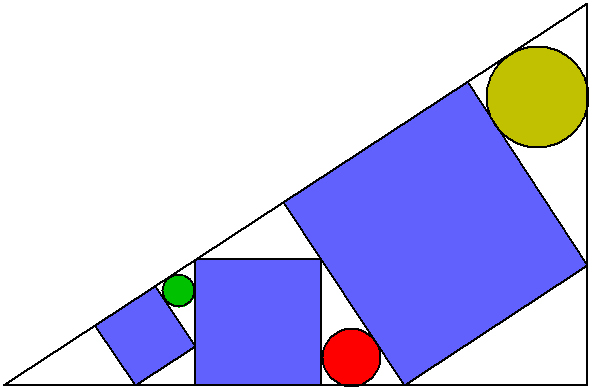 |
Suppose you live on an island that is shaped perfectly like an equilateral triangle. This island is covered in thick vegetation, which makes it hard to move across. However, it has perfect shorelines: beautiful, white sand, crystal blue water, and no commercial waste. Now, if you're like me, you want to spend as much time on the beach as you can. So, naturally, you want to build your house at a spot on the island that minimizes the total distance you have to walk through the island's vegetation to get to each of the three shorelines (that way, you destroy as little of the island's delicate ecosystem as possible). Where should you build your house? Assume that you can build your house at any point on the island, and there are no crazy topological features (mountains, ravines, piranha-infested rivers, etc.) to get in your way.
Two houses stand on opposite sides of a river whose banks are parallel. Where should engineers construct a bridge, which must be perpendidular to the banks, so that someone going from one house to the other will have to travel the shortest possible distance? You may not assume that the houses are the same distance to their respective banks; as a matter of fact, your solution must be independent of the distance that the houses are to their respective banks.

Imagine an old pirate island. There is a gallows on this island, and only two trees. Thereís also a treasure buried somewhere on the island. The pirate who buried it did it thusly: Start at the gallows, walk to the first tree, turn 90 degrees, and then walk the same distance as was the gallows to the first tree. Mark that spot A. Repeat this with the second tree, except turn 90 degrees in the other direction. Mark this spot B. Find the midpoint of AB. Thatís where your treasure is.
Years later, the pirateís heir returns to collect the treasure, armed with the instructions. However, the gallows is gone. Can he still find the treasure?
Find the smallest positive integer such that one-half of it is a perfect square, one-third of it is a perfect cube, and one-fifth of it is a perfect fifth power...without using a computer.
1. Take any three-digit number with different first and last digits.
2. Reverse the order of the digits to get another three-digit number.
3. Subtract the smaller from the larger to get a new number. If you get a two-digit number, write it with a zero in the hundreds' place.
4. Reverse the order of the digits of your new three-digit number.
5. Add the numbers from steps 3 and 4, and explain why the answer you always get is 1089.
Farmer Bill weighed hay for his cows every day, using a 40-pound rock and a balance. One day his neighbor, Bob, borrowed the rock. When Bob returned the rock, he had to confess that he had dropped it and broken it into four pieces. Interestingly enough, Farmer Bill and Bob discovered that with these four pieces, any weight from 1 pound to 40 pounds (whole pounds only) could be accurately measured. Which four weights for the pieces would make this possible?
Imagine a row of 1000 lockers, all closed, and a row of 1000 men. The first man goes through and opens all of the lockers. The second man, starting with locker #2, closes every other locker. The third man, starting with locker #3, changes the state of every third locker (if it is closed, he opens it, and vice versa). They continue this until the 1000th man changes the state of the 1000th locker. After all 1000 men have passed through, which lockers are open?
Imagine a circular room of 1000 lockers, all closed, and a row of 1000 men. Locker #1000 is adjacent to locker #1 in the circle. The first man goes around and opens all of the lockers, stopping after he has opened the 1000th locker. The second man, starting with locker #2, goes around and closes every other locker, and stops when he closes the 1000th locker. The third man, starting with locker #3, goes around and changes the state of every third locker (if it is closed, he opens it, and vice versa), stopping after he has changed the state of the 1000th locker (Note: some men will have to go around more than one time). After all 1000 men have passed through, which lockers are open?
Figure out how this works. If that link doesn't work, try downloading and extracting this.
1973 was a great year. The world's population was still below 4 billion, the Ramones formed, American Graffiti came out in theaters, which paved the way for George Lucas to give us Star Wars...but what I'm really interested in is the hundreds' digit of the following sum:
So tell me, what is the hundreds' digit of that sum? (...of course, you'll first have to figure out what those exclamation points mean...)
King Arthur wanted to decide who was the fittest to marry his daughter, and chose this method. When all his knights were seated at the round table, he entered the room, pointed to one knight, and said: "You live." The knight seated next wasn't so fortunate. "You die," said King Arthur, chopping off his head. To the third knight he said: "You live," and to the fourth, he said: "You die," chopping off his head. He continued doing this around and around the circle, chopping off the head of every other living knight, until just one was left. This remaining knight got to marry the daughter, but, as legend goes, he was never quite the same again. Find a pattern so you can predict where to sit (to live) no matter how many people are seated in the circle.
A natural number is said to be palindromic if reversing the digits leaves the number unchanged. For example, 1331, 7, and 202 are palindromic, but 220 is not. Find the 2000th palindromic natural number, without using a computer or calculator.
1. Choose any 3 digits from 1 to 9.
2. Form all of the 2-digit numbers you can from these.
3. Add up all of these 2-digit numbers.
4. Add the three original digits together, and divide them into the sum from step 3.
Explain why the result of step 4 is always 22.
How many ways can n identical objects be put into n identical boxes so that exactly one box is empty?
Anne and Brian play the following game with a deck of nine cards...Anne plays first and then they take turns to remove one, two, or three cards from the pack, but never the same number as the previous player. The winner is the one who either takes the last card or leaves the other player with no valid move. Who will win? Assume that both players are trying to win, and not just randomly selecting cards.
| I have a game for you and I to play. We each pick a six-sided die from the list of dice at right and roll it; whoever gets the highest number showing wins. If you lose, you pay me $2, but if I lose, I have to pay you $3. Pretty cool, huh? Hey, you even get to pick your die first! So, what do you think? Will you play this game? | Die 1 has three 1's and three 5's Die 2 has four 2's and two 6's Die 3 has six 3's Die 4 has four 4's and two 0's |
| Suppose that you have an equal number of red and blue points in a plane, with the
condition that no three of them are collinear. Shown at right is an example
of this with 5 red and 5 blue points. Now, suppose that you connect each red dot to a blue one with a straight line. Prove that, no matter how many dots are used, as long as there are an equal number of red and blue dots, and no three dots are collinear, it is always possible to connect the dots in red/blue pairs with segments so that no segments cross. |
 |

Now, I want you to focus on one of those six cards. Think about it very hard (for Pete's sake, don't use your mouse pointer!) Do you have it committed to memory? Good. Go here for the next step...
How many times, on average, would you have to roll a die until you see each face at least one time?