Kinematics Practice....
What we developed previously from integrating Newton's 2nd Law in a number of different contexts gave us the following general results:
When a = 0!
x(t) = x0 + v Δt
When a = Constant!
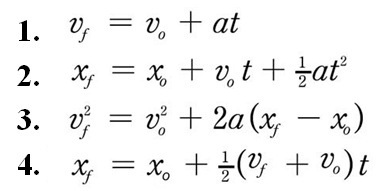
Be aware that #3 is just #2 substituted into #1 replacing "a" and doing a lot of algebra:) #4 is a statement that the average velocity (constant over the interval) halfway between the initial and final velocity WHEN a = constant!
When a NOT Constant!
- go forth and integrate using methods from previous breadcrumbs.
Sample Settings:
We'll use the usual problem solving frame as a framework for our solutions. For a more focused set of strategies see this description of the process for addressing all variations of kinematics problems. This can be summarized as sketch, simplify (clearly state assumptions), represent various ways, express mathematically, solve, and evaluate for reasonableness.
You want to throw a ball straight up into the air so that it reaches a height of 5.3 m above the ground. You may take it as a given that the acceleration of the ball is 10(m/s)/s downwards and constant. Assume the ball leaves your hand at a height of 1.2 m above the ground.
...and a real application of physics.....
When we are driving a typical reaction time is 2/3 of a second. When we are driving 8 m/s (30 km/hr or 20 mi/hr) our typical stopping distance is 12 m including the reaction time. What does this suggest will be our total stopping distance when we are driving 12 m/s (45 km/h or 30 mi/hr)? Follow the process and examine/state the various appropriate assumptions you need to make to answer this question. Hopefully this explains why the folks in blue come down so hard on us when we are going a little fast in school zones.
What we want to explore now are situations where there are multiple objects. Our approach to sorting this out will remain the same -- sketch, simplify (clearly state assumptions), represent various ways, express mathematically, solve, and evaluate for reasonableness.
Here's a problem of this type....
A student, who is running to catch his bus, sees the bus start to pull away from the stop. He is 20 m away from the stop and running at his top speed of 5 m/s. The bus is old and can only accelerate at 1.5 m/s2.
In classical physics problems there would be an explicit question attached to the end. Indeed, where I stole this problem from there was such a question. Part of what we are trying to develop in this class is the ability to recognize the potentially interesting questions that exist in each setting.
This is one of the situations where I am quite unhappy with remote land for learning. In f2f classes we can easily take a few minutes for each part of the process and discuss easily at the whiteboard. Much more aggravating in zoom. We'll try our best but it may be frustrating. We will go out into breakout rooms and back into the class every couple of minutes to discuss each part of the process. My apologies if it turns out to be less that successful.
Activity: Starting with the problem statement above we will walk through each step of the problem solving framework in groups and the gather as a class to discuss briefly. Be aware of the questions that arise as you are working through each step. Many times you can learn more in the breakout rooms by LISTENING carefully to the perspectives of your classmates..
There is some relationship between this setting and the classic xkcd Velociraptor problem:)
This one was posted to Wyzant asking for physics tutor help.....
Two objects are thrown up. Both are thrown up at 16 m/s, but one of the them is thrown up 2 seconds later after the first object is thrown.
The question has been removed to protect the innocent...
Here's aother problem from an MIT physics course:
A car is driving at a constant but unknown velocity, v0 , on a straightaway. A motorcycle is a distance d behind the car. Initially, they are both traveling at the same velocity. The motorcycle starts to pass the car by speeding up at a constant acceleration a . When the motorcyclist is side by side with the car, the motorcycle stops accelerating and is traveling at twice the velocity of the car. How long does the motorcycle accelerate? What was the initial velocity of the car and motorcycle? How far did the motorcycle travel while accelerating? Express all your answers in terms of the given quantities in the problem.
Use the same problem solving frame to set this up and progress. Sketch/translate, simplify, represent mathematically, evaluate, check for reasonableness.
Taken to Extremes:
This sort of analysis can get quite carried away. Dmitri Krioukov, a physicist, argued in court that his ticket for running a stop sign was given in error. It is a complex argument that starts from a simple sketch. You may find his 'Proof of Innocence' an interesting read.
Applications in Engineering:
Here is another application of kinematics and graphing in the real world. This traffic study plot is from Fort Collins Colorado and I know of a COCC engineering student who is currently doing this same sort of work for ODOT here in Central Oregon. Take some time and think about what the meaning of all the different parts of the data are. Are the lights equally spaced? I've driven this street and you would think that a light every other block would be perfectly uniform.

HW: Kinematics Applications
A stationary car is initially some distance behind a stopped truck. Both begin to accelerate simultaneously. The car accelerates at 1.8 m/s/s and the truck at 1.2 m/s/s. The car passes the truck when the truck has traveled 48 m. How long did it take the car to catch up to the truck? How far behind the truck did the car start?
[9 s, 24 m]
HW: Kinematics Applications
Let's apply these ideas to a real life situation. Imagine the traffic on the parkway is moving along at a steady speed of 20 m/s (a little over 45 mph). Your car can accelerate from 0 to 30 m/s in 11 s. Assume it takes 3 sec after the lead car passes to pull out into traffic where your initial speed is 5.0 m/s.What would be meaningful to figure out here - how far apart do the cars have to be for this to be safe for you? Start by figuring out whatever you can and see if you can build a pathway to an answer. Focus on process and answers will come.
[2.7 (m/s)/s, 8.5 s, 102 m]
HW: Kinematics Applications
You are at a supermarket in Seattle and the parking lot is quite sloped. As you get out of your car you notice a shopping cart escape from a dad trying to manage kids and the cart simultaneously. The cart is 20 m downhill from you and has an acceleration of 0.5 (m/s)/s. You spring into action with an acceleration of 2.0 m/s/s with a maximum speed of 8 m/s. How does our tale end? Do you catch the cart? Where and when? What happens then?
[5.4 s and 7.2 m from dad]
HW: Kinematics Applications
A woman in an apartment sees a flower pot fall past her window. She observes that it takes 180 ms for the pot to traverse her 2.3 m tall window. Where did the pot start falling from (at v=0!)? Undoubtedly the woman will report the resident of the appropriate apartment to the building super for poor cleaning habits. This is a problem which benefits from observing all the steps in the problem solving framework.
[1.2 s, 7.2 m up]
HW: Kinematics Applications (optional - replaces two of the above problems)
(Calc) The NASA shuttle has a weight of 93.106 N and generates a constant thrust (force) of 90.106 N during the firing of its main engines and solid rocket boosters. While the engines are firing fuel is being consumed at an alarming rate which reduces the mass at a rate of 5.7.104 kg/s. When will the shuttle actually begin to lift off the ground? What is the velocity of the shuttle 40 s (assuming all these numbers are valid) after the shuttle begins to rise?
Assignment: HW: Kinematics Applications
Turn in the various (4 or 3 if you do the calc problem) homework problems in this breadcrumb. For these problems please use the problem solving format described in the Concepts breadcrumb.
Assignment: Reading
From here we take our knowledge of Newton's Laws, vectors in 2D, and kinematics and head off to the world of 2D Newton's Laws problems. Sketching becomes ever more important as we involve multiple objects, friction, and ramps. Newton's 2D breadcrumb.
