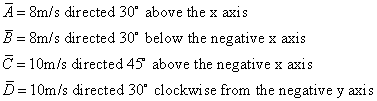NOTE: Because of all the images this page violates good web design principles and is quite long. Hang in there all the way to the end!
Just a reminder where the vector simulation tool is.
In a Just Universe.....
A thought to start with: In a just universe the rules for vectors in 1D should apply identically in 2D and 3D (and more than 3 actually). We may have to broaden our understanding of certain features of vectors but there ought to be some consistency about the processes. This what mathematicians are particular good at. It is relevant to note that mathematicians have developed many new tools over the centuries and it is remarkable at some level that, in almost every case, the science community has discovered that those new tools are perfect for describing some previously unclear behavior of the universe. Quite remarkable.....
Graphical Addition: 2D
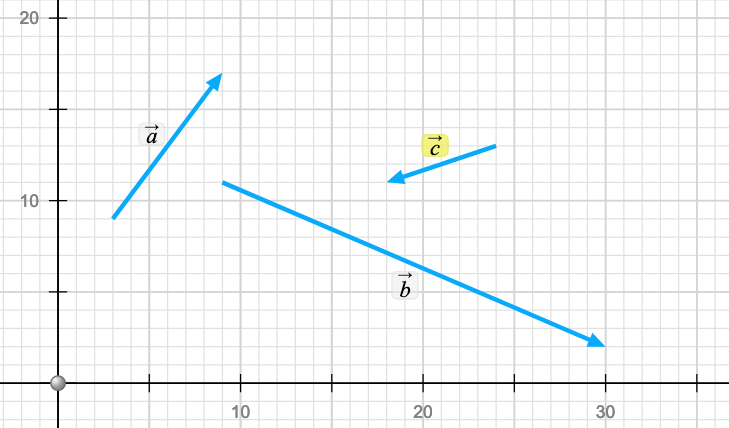
Let's return to the PhET simulation and move to the 2D exploration tool. Grab three vectros from the tool bar and drop them anywhere on the grid. Ideally 3 different lengths and directions. Once you've dropped them on the grid add them up using the tip to tail method. Show that A + B + C = B + C + A = C + A + B etc etc (I've replace the lower case vector names with upper case for clarity). This means the end of your chain is the same distance from the beginning of the chain in each case. Here are my vectors..
A + B + C
C + A + B

Reexpressing Vectors: Why?
Consider the sum 13 + 7 = ??. Almost all of you will mentally take the 13 apart into 10 + 3 and then regroup the terms to get 13 + 7 = 10 + (3 + 7) = 20. I may be overstating it a bit but you're perfectly comfortable seeing it this way. We reexpress numbers this way to simplify our calculations when it's convenient. We are about to do the same thing with vectors. An important starting point for this discussion to be certain that you accept that when I say x + y = 15 there are an infinite number of possible values for x and y. When I say C = A + B the same thing is true. There are an infinite number of pairs of vectors that will add together to give me C. Like the numerical example earlier we will choose which A and B we want to use based on convenience.
Perpendicular Components:
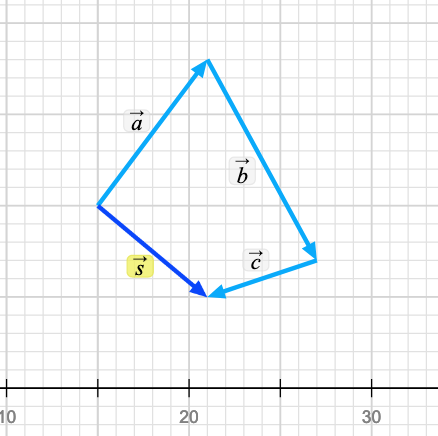
The first convenience we will apply as we reexpress our vectors is that we will express C as just 2 other vectors. Lets call them C1 and C2 for now. Mathematically C = C1 + C2. The next convenience we will apply is that C1 and C2 be perpendicular to each other. There are still many many possibilities here of which just 2 are shown below.
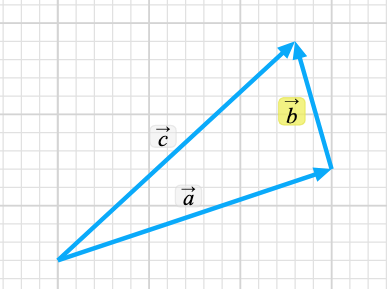
We call the two vectors which add together to give my vector of interest (C) the components of C (in this case a and b) The standard interpretation of the components of a vector is that they are perpendicular to each other.
In a Coordinate System:
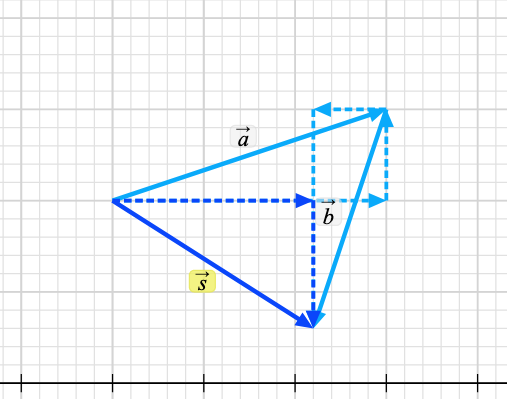
The final convenience that we apply to our choice to represent C with components is to align each component with the axes of our coordinate system. For now we will work in the x-y system but eventually you will work with components in other coordinate systems. If you select one of the component representations in the simulation menu the components in the x andy directions for each vector will be shown as dotted lines. Start with one vector, add a second, and then consider the sum of those two.
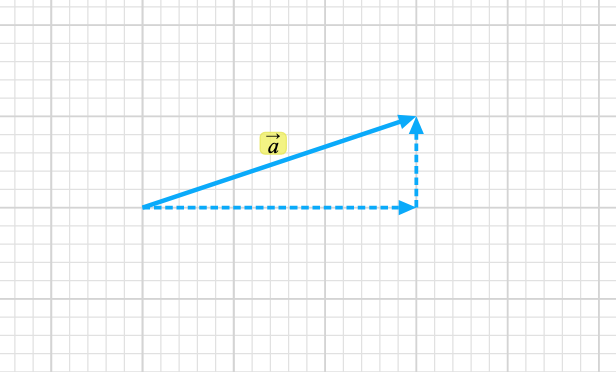
We would write this mathematically as A = Ax + Ay where the vector Ax is represented by the horizontal dotted line and Ay is represented by the vertical dotted line. Note that the directions of the components are critical. Don't leave them out.
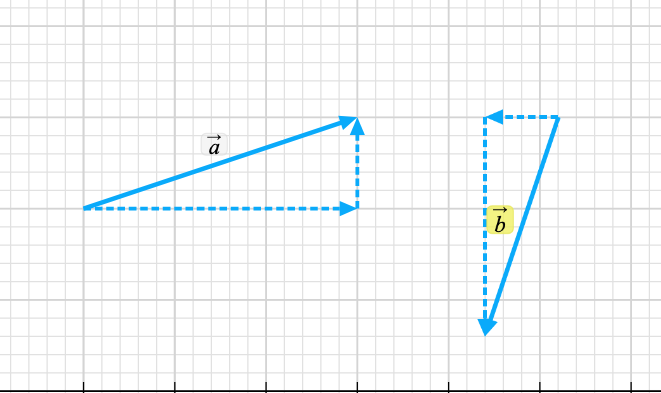
Now we add B = Bx + By to the mix. Now we add A + B = (Ax + Ay) + (Bx + By) = (Ax + Bx) + (Ay + By) = S.
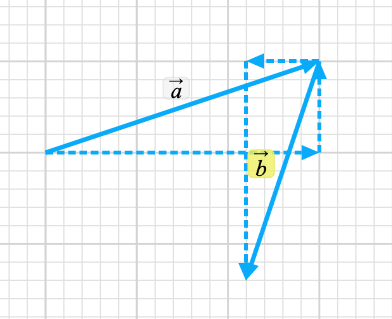
Perhaps you will notice that this turns the some of two vectors into the sum of 4 components but the components can be rearranged to be 2 1D problems. A 1D problem in the x direction giving us Sx= (Ax + Bx) and Sy= (Ay + By).
Trigonometry and Pythagoras:
Because the components of each vector are perpendicular to each other and the vector is the hypotenuse of the right triangle the lengths of the vector and it's components are related by the pythogorian theorem.
|B|2 = |Bx|2 + |By|2
From past math classes (pre-calc or trig - MTH 112) you are aware that when we have right triangles the ratios of the lengths of the various sides are defined as the trig functions sine( θ), cosine(θ), and tangent( θ) which are generally abbreviated sin( θ), cos(θ), and tan( θ). You are expected to know these trig functions and their use in right triangles like the back of your hand. The reality is that you're probably not that secure right at the moment but you need to practice quickly to be solid with them.
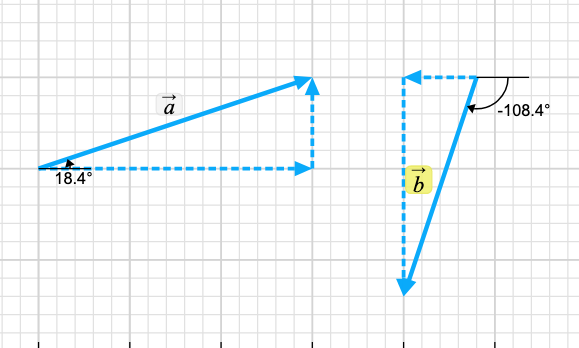
|Ax| = |A|cos(θ), θ = 18.4o or |Ax| = |A|sin(α), α = 71.6o, + in this coordinate system
|Ay| = |A|sin(θ), θ = 18.4o or |Ay| = |A|sin(α), α = 71.6o, + in this coordinate system
Activity: Find the components of B (assume |B| = 2.4 m if you need to).
Here's a short video showing the process of going from a vector to it's components.
Here's a video showing the process in the other direction -- getting the vector when you have the components.
Unit Vectors:
Unit vectors are a central tool for working with vectors in all the sciences. Their purpose is to separate complex problems in multiple dimensions into individual 1D problems which we can 'solve' algebraically. So what is a unit vector? It is a special kind of vector which has a defined length of 1 and points in a particular direction. If I label the unit vector in the x direction i then..
Ax = |Ax| i = Ax i
Its a little hard to see with the type on a webpage but Ax = |Ax|is just a number representing the magnitude of the vector Ax and it's sign tells us the direction relative to +x. 3 N i is a vector length 3 N pointing in the +x direction. -3 N i is a vector of length 3 N pointing in the - x direction. Notice that the unit of the lenght does not have to be a 'distance'. Any vector in the x direction can be written as some multiple of i , the unit vector in the x direction.
Unit vector notation:
There are a variety of different notation systems for unit vectors. We will most commonly use the i, j, k notation system for the unit vectors in the x, y, and z directions respectively. Below are the most common notations for the unit vector in the x direction.
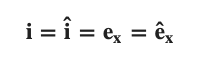
What you need to take away from this is any symbol with the 'hat' - '^' over it is probably a unit vector. This is not easy to do on a webpage so we typically use the boldface i, j, k notation. The e with a subscript is another very common notation for a unit vector that you need to recognize.
Orthogonality: Draw a vector that is 2.4 units long in the y direction ( 2.4 j). Can you describe any part of this as some multiple of the i unit vector? Why or why not? This is a version of what we mean when we say two vectors are orthogonal. This is a slightly more complicated idea than perpendicular but it's close. You are perhaps aware that almost all coordinate systems are characterized by the fact that each coordinate direction is perpendicular (orthogonal) to all the others. This leads to each direction being independent of the other directions which allows us to generally treat that part of the problem as a 1D vector problem.
Activity:
Draw two vectors Ax = - 4 i and Ay = 3 j and add those two vectors to get a vector A using the graphical ideas we explored at the beginning of this page. You can do this sketching on a piece of paper. What is the length of the resulting vector? (hopefullly you get 5) What are the angles in the corners of the resulting triangle? Remember your trig? We can write the mathematical decription of this process by saying A = 4 i + 3 j = Ax + Ay.
4 i and 3 j are called the vector components of A in the x and y direction. Notice that any operation that only affects the x component has no effect on the y component etc etc. Note that this would not be true if x and y were not orthogonal directions. This is sometimes written as A = Ax + Ay= A xi + Ayj = 4 i + 3j. These are all equivalent ways to write and describe the vector A and it's components.
Note for the Future (MTH 254):
i can be written as a generalized 2D vector as (1,0) and j can be written as (0,1). A can be written (4,3) meaning it's 4 units long in the x direction and 3 in the y. In math 254 you define an operation called the dot product. i . j is written (1,0).(0,1) which = 1*0 + 0*1 = 0! This is the definition of orthogonal. (1,0,0), (0,1,0), and (0,0,1) are three directions that are also orthogonal (we usually call them x, y, and z). How would you write 4 vectors in 4 dimensions that are orthogonal? Can you visualize this?
Knowledge at Your Fingertips:
Some numbers come up again and again in math and science and over time they should become easily accessible to you without reaching for your calculator. It would be a great plan if you would slowly learn the sin( ) and cos( ) for the following angles (0o, 30o, 45o, 60o, and 90o). Be sure you also know the 3,4, 5 right triangle geometry.
Online Resources:
I am aware that many students prefer to access information like our discussion about vectors via videos. I have linked some possible resources here. Be a little careful. They all use their own slightly different notation or way of thinking about vectors that doesn't always align precisely with my discussion above.
Here's a great alternative starting place from the Physics Classroom
I encourage you to try this interactive vector page to practice quickly adding two vectors in your head. On the hard setting it's challenging to solve the problems before time runs out. I'm a little frustrated that they call it a guessing game but hey -- I didn't spend the energy to create it so I don't get to complain.
This document gives you a slightly more formal treatment of vectors and does one version of unit vector notation.
Finally, here are some good example problems using 2D vectors in kinematics some of which are related to typical homework problems.
HW: Vectors 2D
What are the x and y components of each of the following vectors? I recommend doing this graphically first to clarify your estimates (which component to you expect to be bigger) and then compare the results to those you calculate. Use signs to indicate the direction of the component relative to YOUR labeled coordinate system.
[A: 4 m/s, 6.9 m/s, D: -5 m/s, -8.6 m/s]
HW: Vectors 2D
Given vectors A and B below determine the magnitude and direction of C=A+B, D=A-B, and E = A/2-3B? Do this first using graphical tools and without being too detail oriented. Compare this first result to that which you get by using component methods.
A = Ax + Ay where Ax = 4 and Ay = 6
B= Bx + By where Bx = -10 and By = +2
[C: 10, 53o, D: 14.6, 16o, E: 32.05, -6.1o]
HW: Vectors 2D
Suzie leaves her car and heads off due South for 2 km for a weekend hike. After 40 min she spies a cool rock formation off to the Northeast. She heads directly Northeast for 3 km and has lunch at the rock. After lunch Suzie strolls North for 1 km. On coordinate axes make a reasonable scale drawing of these vectors and estimate the direction and distance she needs to travel to get back to her car. Then calculate the magnitude and direction of that vector.
[2.44 km, 28 degrees S of W]
HW: Vectors 2D
Kayakers and canoeists know that by choosing their direction carefully they can move laterally back and forth across a river without moving upstream or downstream. Assume that the 25 m wide river is flowing at 2.0 m/s and the kayaker can maintain a speed of 3 m/s relative to the water. Be aware that the velocity of the kayak relative to the riverbank is the vector sum of the velocity of the water and that of the canoe or kayak (same is true of planes as well) What direction should you paddle to move directly across with river and how long will it take? How long does it take to cross the river if you paddle directly towards the far shore? How fast will you be going in this second case and where will you reach the far bank?
[about 40 degrees upstream and 11.2 s, 8.3 s, 3.6 m/s and 16.6 m downstream]
Assignment: HW: Vectors 2D
Turn in the various (4) homework problems in this breadcrumb. For these problems please use the problem solving format described in the Concepts breadcrumb.
Assignment: Reading
Next we move on to describing the motion of object using kinematics. We will approach this from two perspectives in the Kinematics from Newton breadcrumbs. We can develop these tools either using integration or graphical techniques.