Uniform Circular Motion
This is an application of Newton's Laws that shows up so often it seems appropriate to treat it as a separate exploration. If you are looking in some standard physics text this will usually be a section within the Newton's Laws chapter.
'New' Concepts/Language:
There are number of ideas or concepts that you have heard before and possibly worked with somewhere in your mathematical past. The first of these is the relationship between angle and arc length as well as angular velocity and tangential velocity. The second of these are the related concepts of period and frequency.
Angles and Arc lengths:
It is customary when objects are moving angularly to describe their angular position using radians. This is because there is a smooth connection between angular and linear variables when the angles are measured in radians. We can do it in degrees but then we end up have lots of confusing factors 2π and 360o running around.
Here's how it starts...
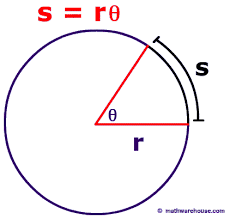
s is the arc length (in m) and r (also in m) is the radius. θ (in radians) is define to be s/r. Looking at the units that means a radian (rad) = m/m = 1. This is a confusing/irritating feature of radians in that they have no units in the normal sense. This makes the unit appear and disappear in mysterious ways.
What if we now differentiate this expression for θ? dθ/dt = r ds/dt since r is a constant. ds/dt is the rate of change of position along the arc which is the linear speed velocity (speed) along the arc. This is often labeled vT for tangential velocity. dθ/dt is rate of change of the angle which is called, not surprisingly, the angular velocity. The usual symbol for angular velocity is ω (called omega). This gives us the following important relationship between ω and vT.
vT = r . ω
For those who want to practice you can take one more derivative and find that the angular and linear accelerations have a similar relationship. (the angular acceleration is alpha)
aT = r .α
Take Home:
Begin to generate a confidence that when you have an object traveling along a circle that it doesn't matter whether you know the linear velocity vT or the angular velocity ω since they are just slightly different versions of the same thing. We all start out thinking of them as very different and yet they are closely related.
Period and Frequency:
 25 Hz, 0.04s
25 Hz, 0.04s
Many objects which move in circles are cyclic in their behavior. The earth goes around the sun in a cycle that repeats annually. The shaft of a engine or a motor spins cyclically. The period is the name we give to the time it takes to complete one cycle. The customary symbol is T (for now) and has units of seconds. We often think of this as T= s/cycle though we don't include the cycle as a unit. What is the period of the earth's cycle in s?
When cycles are very short our brains often find it easier to understand how many cycles there are in some period of time. Sound is an example. Middle C on the piano is a sound which has a period of 0.004 s (pretty close) which is not easy for most of us to visualize. For whatever reason the idea that this is 250 cycles each s (cycles/s) is somehow easier to understand. This is what we mean by frequency. Frequency is often indicated with an f though there are other symbols that are commonly used where f might cause confusion. f has units of 1/s or s-1. This unit, s-1, is so pervasive that it has it's own name and is called Hertz and is abbreviated Hz.
You will no doubt notice the T = 1/f and f = 1/T. They are inverses of each other mathematically.
Another description of frequency is RPM which is an acronym for revolutions/minute. Can you show that 600 RPM is the same as f = 10 Hz and T = 0.1 s? What are f and T for an object rotating at 1500 RPM?
Acceleration of Object Moving in a Circle at Constant Speed:
When we are f2f I often explore both the geometric and calculus approaches to this setting. If we don't do it in class or you want to see it again I have embedded two videos below that walk through both a geometric and calculus 'derivation' of the acceleration of such an object. Here's the starting point to have in your mind before you go watch either or both of them.
In calculus we typically start learning about velocity and acceleration in one direction like the x direction. This leads to definitions of v = dx/dt and a = dv/dt which illustrate the rates of change but not their intrinsic vector nature. We commonly use x to describe a position along the x axis when in reality, in physics, we are actually using a vector which is either in the +x or -x direction and has some length. x is really x - a very subtle difference between bold and not bold in the text! That means
v= dx/dt
..where v and x are both vectors (t is a scalar but web fonts don't handle this well). In a 1 dimensional system x can't really change direction other than to reverse direction. In a more general sense we describe the position using a vector called r which has a length and a direction like r in polar coordinates. If we write the definition of velocity using this more general position vector we get....
v= dr/dt
Now you can imagine a object described by the r vector which stays the same distance from the origin but changes direction. This is a description of something moving in a circle. r is staying the same length but because it's changing direction there is a velocity. I suspect this doesn't bother you much but remember this object only has a velocity because the vector which describes where it is in changing direction but NOT magnitude.
Now consider....
a= dv/dt
We are used to thinking of objects that accelerate when the magnitude of v is changing (speeding up or slowing down) but we now have an inkling that something can be traveling the same speed (magnitude of v) and still have an acceleration because the direction of v is changing.
Here is a nice video from Matt Anderson illustrating a very graphical approach to determining the acceleration of an object moving in a circle. It's about 9 min if you don't get distracted by the cool presentation tools he uses.
Here is a Khan Academy video that derives the centripetal acceleration from a calculus perspective by defining the x and y components of the position and then taking derivatives. It's a little longer (14 min) but also does a nice job. For those of you who prefer a written exposition of the calculus method here is a document that does a nice job.
Take Home:
When an object moves along a circular path there is an acceleration, ac, given by this expression:
ac= v2/r = rω2
There are a host of ways to think about what this means as you progress through your academic career. At this early stage of your learning I think it is helpful to avoid language that, in my experience tends to confuse and obscure rather than help. As a result there are certain words and descriptions associated with circular motion that Wendi and I have chosen to NOT use. I will not even mention them here.
What we have done is take the actual kinematic description of an object moving in a circle of some radius with a constant angular and tangential velocity and shown that such an object must have an acceleration of v2/r (or rω2) . By careful examination of the components of the acceleration we can see that it points directly towards the center of the circle. From Newton's 2nd Law we know that if an object has an acceleration there must be a net force in the direction of that acceleration. Your intuition may wish to dispute this but as you explore a variety of problems notice that Newton's Law offers a consistently successful tool for describing circular motion. Explore your sense of unease about this as we go through various problem settings and you will have the best chance of slowly developing a more effective understanding. It's all about Newton's Laws....
WARNING:
This acceleration is called the centripetal acceleration and is usually/often abbreviated ac. Moving in a circle does NOT create any new forces! Many students want to add a new force to their freebody diagrams. Resist this urge! For now there is gravity and everything else is a contact force that produces the force on your object of interest. Centripetal force is not a thing never mind the other force whose name may not be spoken.
First Exploration:
Consider the following setting for a mass on a frictionless table. Start, as we always do with a freebody diagram.\
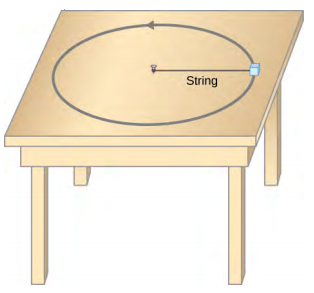
Activity: Compare your freebody diagram to others in your group. How did you each choose to represent the forces on the mass which occur in 3D? What can you say about the forces in the vertical direction from Newton's Law? What force on your freebody diagram must be responsible for the ac?
Here is one possibility for the freebody diagram but it doesn't indicate which way the mass is moving does it?
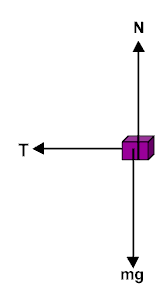
HW: Circular Motion: ac
The International Space Station (ISS) completes an essentially circular orbit around the earth every 90 min. Given that the ISS is 400 km above the surface of the earth on average what is the centripetal acceleration of the ISS and it's inhabitants? What force on your freebody diagram might produce this acceleration?
HW: Circular Motion: ac
When you make a left turn at an intersection of a 4 lane road you are traveling along a circular arc with a radius of 15 m. Assuming, on dry pavement, that you can do this at 10 m/s (20 mph) what is the centripetal acceleration of your car and you? What force(s) on the freebody diagram of your car could be responsible for this acceleration?
HW: Circular Motion: ac
At one point the fastest CD-ROM drives spun at around 10,350 RPM for a 120 mm diameter CD. Perhaps CD's went the way of the dinosaurs before you were aware of them but you occasionally see them around still. What is the centripetal acceleration of a bit of the CD at the edge when it is spinning at this speed? What force(s) could be responsible for this acceleration (this is a fuzzy question so don't get wound up)?
HW: Circular Motion: ac
Determine the radius of the orbit and the speed of a geostationary satellite. Such a satellite remains located over the same geographic point on the earth as it rotates. You will need to look up Newton's Universal Law of Gravity (in the Newton's Laws 1D II breadcrumb), and consider its impact on your freebody diagram, and various other constants in your book. You will need to consider the relationship between the period and the speed and the radius as well. In Newton's Universal Law of Gravity the relevant radius is from the center of the earth. You may ignore all other gravitational forces:) You can get some sense of what your result will be from this image of space junk near the earth. The geostationary orbit is the crisp circular ring of debris some distance from the earth.
Assignment: HW: Circular Motion: ac
Turn in the various (4) homework problems in this breadcrumb. For these problems please be attentive to our problem solving format and guidelines for different styles of problems.
Assignment: Reading
Next time we will go on to explore a consistent methodology for setting up and solving circular motion problems. Read Circular II Breadcrumbs.
