Mood Brightener: ...more from Stay Homas. (Confination III)

 

Your Conceptual Goals for this section: Coulomb's Law

Coulomb's Law:

The upshot of our initial explorations about charge using tape, balloons, and electroscopes have hopefully resulted in some confidence about the following statements:

3rd Grade Rule: Like charges repel each other and opposite (unlike) charges attract each other.

The electrostatic force is very (strongly) distance dependent.

Charged objects are attracted to neutral objects (an understanding of polarization provides an explanation)

Conductors are materials that allow (typically) electrons to move, insulators do not allow charge movement

Only electrons (- charge) actually move in solid materials but + charge appears to move identically

Most materials are charge neutral with loads of + and - charge; 1000's of Coulombs.

Charged objects have relatively small amounts of unbalanced charge resulting from addition or removal of electrons

A natural place to seek to understand more deeply is to ask if there is a predictable way to calculate the force between two charges. In the same way that Cavendish sorted out the rule governing gravity Coulomb determined that the magnitude of the force depended equally on the magnitude of both charges (suggesting the product of the charges) and inversely on the square of the distance between the charges. Here's what it looks like....

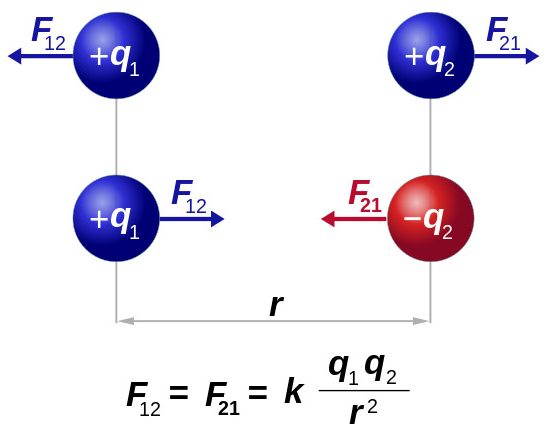
This version of Coulomb's Law describes the magnitude of the force not the direction. We will discuss how to make this a vector law. For us it will be most useful to describe the magnitude and use our understanding of the 3rd rule to assign direction.

The propotionality constant - k - is determined experimentally. k = 8.99 10⁹ Nm²/C². For our purposes we'll just call it 9 10⁹ Nm²/C².

NOTE ABOUT k!:

I have chosen to express Coulomb's Law in this form because it matches the form of Newton's Law of Gravity. As usual, due to the historic timeline for the development of these ideas, there is another form of the equation which you will come across for sure. Another version of the constant is often written as 1/4πε₀. ε₀ is known as the permitivity of free space and has a value of 8.854 10^-12 C²/Nm². The 4π comes from the recognition that when we are integrating over spheres as often happens in electrostatics there is often a factor of 4π from the integral which is cancelled by this term. It just the way the physics community defined it. We will use k since it keeps the visual clutter to a minimum.

[insert video problem set up here]

Net Force Problems:

Here's a typical Coulomb's Law problem:

q₁, q₂ and q₃ are +8.00 μC; -5.00 μC; +5.00 μC respectively

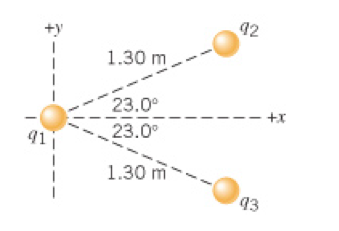
If we'd like to know the forces acting on any of the charges where do we start? Please tell me you would naturally go and make a freebody diagram for each charge! A decision that often has to be made is whether gravity is a player in these problems. In the absence of clues that suggest gravity is a player in the problem (one block is floating above another maybe?) you may choose to imagine this is taking place without gravity. As we consider this problem we will also calculate the gravitational force on one of these objects and see if it's actually relevant.

For reference a grain of sand is about 60 μg and a pollen grain is about 6 μg.

We will go through this solution in real time during class but I include a video for future reference here. Before class just look through the questions below to be sure you understand the sequence of questions we will be addressing.

[place holder for video]

Starting with q₁:

In your freebody diagram can we make some useful statements because of symmetry?

What is the net electrostatic force? How does this compare to the force of gravity on a grain of sand or a pollen grain?

Now working on q₂:

How far apart are q₂ and q₃?

Small angle approximation discussion:

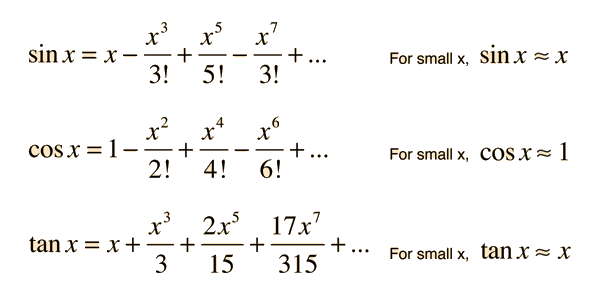
What do the x's represent? Degrees or Radians? Calculate the first 3 terms if x = .1 rad. How much error do we introduce by only keeping the first term? What qualifies as a small angle? This will be relevant on the homework.

How does this help with this part of the problem? Is 23 degrees a 'small' angle?

Now working on q₃:

Do we have to do this problem separately? Why? -- how do you make the argument from symmetry?

Integration:

Electrostatics is a natural place to start developing a sense for how integration problems are setup and executed in the science and engineering world. Imagine I have a plastic rod which has charge distributed evenly along it's length. At a distance 'a' from one end there is a point charge q. Do physics!

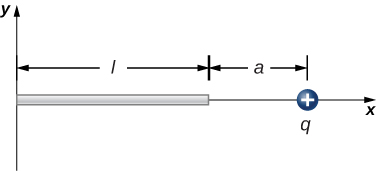
The process we will follow for addressing these sorts of problems will follow this integration process.

If we have time we'll consider a uniform ring of charge....

Assignment Breadcrumb Reading: Bb Test

Coulomb's Law!

Two small spherical water drops have charges of -10 nC and a separation of 1.0 cm. What is the electrostatic force between them and how many excess electrons are there on each drop?