Mood Brightener: ...more from Stay Homas. (Confination V)

 

This will be mostly a qualitative discussion of E fields

Your Conceptual Goals for this section: E Fields

Fields (electric or otherwise):

The question of what a field is and why we need these beasts is a actually quite rich. We will explore some of the philosophy behind this concept in class but if you would like some reading on the topic here are some suggestions.

stackexchange: This is a great discussion of physics as equivalent in some way to trying to understand the 'code' of the universe. Here is one of their threads addressing the concept of fields.

Here is a longer pdf document walking through the history of fields as an idea and the motivation. You will need to form your own understanding of what fields are and why they are valuable as a concept if not a reality.

Here's the thought exercise we will discuss. If the sun were to start moving in some new direction how long would it take for the earth of any of the outer planets to notice the change in the direction of gravity? What are the possible answers? How can you test these different answers? [results of tests will be shared in class]

Electric Field (E):

Regardless of the philosophic roots of the idea of fields we detect the presence of fields by measuring forces (or the behavior caused by forces) on known objects. For electric fields we must use a test object which feels an electrostatic force (Coulomb force). That suggests that the test object would be a charge brilliantly labeled as q_test. I often think of this as my test charge on a string that I keep in my pocket.

We define the E field to be the force per unit of charge (N/C) which can be written E = F/ q_test. You will note that the E field points the same direction as the force on a + charge. We can carry our little test charge all over the world and measure the field at every point in space.

On average there is an electric field near the surface of the earth that points downward and has a magnitude of around 150 N/C.

What is a comparable definition of the gravitational field (not force!)?

Once you know the E field then what?

Once you know the E field at a particular point then you can predict what the force (magnitude and direction) on any charge placed at that point. This charge I like to label as a field charge (q_field) indicating that it is a charge which experiences the field rather than the q_test we used to empirically determine the field.

In this context F_qfield = E q_field which is the value of knowing the E field at that point.

This is very much like knowing that F_g = mg from PH211.

Imagine you have two charges at some distance from each other....

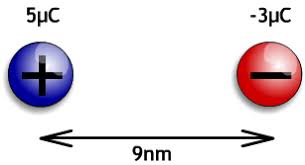
If we treat the +5 μC charge as the test charge can you figure out the E field at that point in space? Do so.....

What about the E field at the location of the -3 μC charge?

Now I replace the -3 μC charge with a +8 μC charge. What is the magnitude and direction of the force on it?

An important conceptual understanding is that at the location of the +5 μC charge there is ONLY a field due to the -3 μC charge. Conversely at the location of the -3 μC charge there is ONLY a field due to the +5 μC charge. Everywhere else there are two contributions to the field, one from each charge. This may seem counter intuitive but as a student said to me once long ago - "You don't smell your own stink". Not a bad model actually.....

As you have no doubt noticed there is a pattern to this....

In this case they use q_o instead of q_test but the meaning is the same. In this expression I would like you to think of the q as the source charge that produces the E field as distinct from either the test charge (q_test) or a charge which experiences the field which can be referred to as field charge (q_field).

Field Representations:

I will no doubt link this math/physics simulation site maintained by Paul Falstad many times in other parts of this class. He really has done a huge service for the physics learning community. Thanks Paul!!

For this section of our course this 3D electrostatics simulation is a great starting point. Set the display to 'Field Vectors' and then explore the many different charge distributions that he has built. Think about the direction and intensity of the field at different points and explore what they look like when you slice them.

You can get a see fairly quickly that trying to sketch or represent the E field can quickly get overwhelming with lots of busy looking vectors all over the place. Michael Faraday, one of the parents of our understanding of EM fields proposed an abstraction of the abstract idea of field called the 'field line model'. We will switch back and forth between the vector representation and the field line representation as we explore the 4 basic fields everyone needs to be able to sketch.

Here are the 4 basic field patterns that every nerd should know.

Single Charge (both + and -):

What do the fields look like around a single + or - charge? How are the vectors different if the charge has a greater or lesser magnitude?

Field Line Model: If we draw a pattern of sea urchin spines we can see that it has many of the same features as the vector representation. How might we intepret the pattern of radial lines as carrying the same information as the vectors?

You will notice that the direction of the field lines and the direction of the E field vectors are aligned. This suggests the first characteristic of field lines is that they are tangential to the field vectors at that point. In addition we can put an arrow on one end of the field line which will indicate the direction of the field vectors.

Then there is the question of field intensity. Where is the E field strongest (largest magnitude of E)? Near the source charge the E field vectors are 'longer' but how do we see a similar feature in the field lines? Generally it doesn't take students long to notice that the closer together the field lines get the stronger the E field they represent is getting. So....density of lines is proportional to |E|.

Finally....it would appear that field lines are connected to their source (at least in the case of E fields). Field lines appear to start at + charges and terminate at - charges.

So here are our 'rules' for the field line representation so far:

i) Lines are tangential to the E field vectors

ii) Lines point in the same direction as the E field

iii) The density of lines is proportional to the strength of the E field

iv) Field lines (for E) originate at + charges and terminate at - charges.

Here is a different electric field simulator from that web page. Place a single + charge in the middle of the screen. What do you notice about the vectors in the simulation? Then stack a couple more on top of it. Does the simulation do the right thing? Compare with Falstad's simulation.

If you want to have a little fun with fields and charges here is a E field hockey game. Simple on first level but gets challenging quickly:)

Dipole Field:

A dipole is a common object to find in the natural world. In it's most basic form it looks like this....

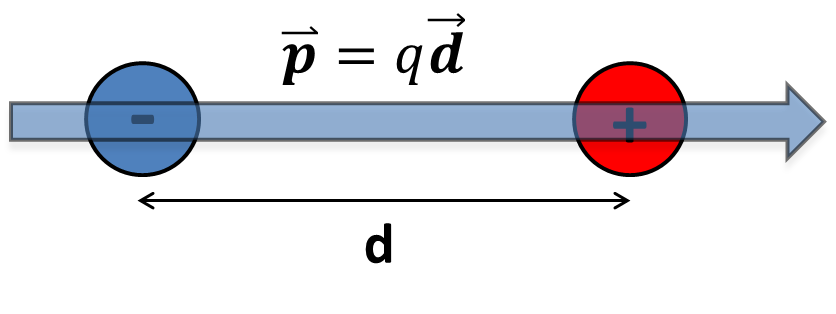
...where the charges are presumed to be of the same magnitude. Sketch a dipole and draw the axis of the dipole (the line that passes through both charges). Now sketch the perpendicular bisector of the dipole (perpendicular to the axis at a point half way between the charges). Pick a point along the perpendicular bisector but away from the axis. Sketch the contribution to the E field from each charge. What do you notice about the symmetry? Is this constant everywhere on the bisector? Consider points near either charge -- is the other charge an important contributor to the total E field near one of the charges? Why?

Now go explore the vector and field line representations of a dipole on the Falstad simulation. What does this look like from magnetism (which we haven't discussed yet but you have had some exposure to)?

Two of the same charge:

Change the charges in the previous picture to be the same sign and repeat the process of exploring the total E field on the axis and on the bisector. What is your qualitative sense of the shape of the E field in this case?

Go explore and confirm on the Falstad simulation!

What you should be able to sketch:

As a competent geek/nerd/science person you should be able to sketch each of these four field configurations (in the field line representation) with confidence....+, -, dipole, two charges (same).

Most fields you will want to sketch are some combination of these four. Here are some hints:

i) Start by getting roughly the right number of lines leaving or arriving at each charge. What's important is that they be proportional to each other and that you have them pointing in the right direction. Don't extend them very far from the charge because this step represents what the world looks like when you're very close to each charge.

ii) Identify which parts of the field sketch should have characteristics of a dipole or a pair of like charges.

iii) Imagine you're far enough from the group of charges to see as just a single net charge. Is there a net + or - charge and how many field lines does that suggest should be arranged around the group of charges.

iv) Connect the interior field lines as appropriate for step ii) with each line originating and terminating somewhere. Then connect the extra lines to your distant view of the situation from part iii). Collectively this should make sense.

[video of triangle of charge]

Assignment Breadcrumb Reading: Bb Test

How to detect an E Field

What is the basic tool by which we detect the presence of an E Field?