Mood Brightener: ...more from Stay Homas. (Confination VI) - this is the one that got them noticed in this country:)
This discussion will be more focused on the quantitative (calculational) tools for addressing the E field.

Vector Sketch:
Like forces fields are also vectors. Not surprisingly then we use that same basic tool to initiate any problem. In Newtonian Mechanics we called it a Freebody Diagram or Force Picture but more generally you should recognize it as a vector sketch. The rule that defines the E field vector at some distance from a source charge is given above. Let us start with a simple seeming problem which has many opportunties for complexity even in 2 dimensions. Let's take a dipole where the separation of the two charges is 1.4 cm and the symmetric charges have a magnitude of 45 μC.We'll solve for the field in several different places for practice
Between the charges of the dipole:
NOTE: I was moving a bit fast and got the E field due to the positive charge in the wrong direction -- crikey!! The two vectors add instead of subtract. Sorry for the confusion I created. The others seem good at the moment. I will fix this ASAP.
Along the perpendicular bisector:
'Above' one of the charges:
Multiple Charges:
Just like the examples above only more fun! Do a vector sketch, sketch the components, determine the magnitude of each E field vector (may need some good geometry and Dr Pythagoras), add the vector components. Done!....if only it felt that simple. My point is that it's a well defined process not that it's easy or quick.
Integration:
Just like Coulomb Force problems in the previous section. Follow the integration frame and don't be thrown off by the fact that there is usually no charge where you are asked to find the field. Practice, practice, practice....
Here are some stills from an example problem Setup, page 2,vector estimation
We also had a quick discussion about whether gravity is generally a consideration in electrostatics problems. The following is a recording of that discussion.
Generally the force of gravity is a small factor in most electrostatics problems and, unless explicitly stated in the problem, can almost certainly be ignored. Be mindful that in general you can choose to ignore any force as long as you state in your solution that you are doing so. You may find the problem is less meaningful or perhaps not. The point is to clearly state your assumptions!
Assignment Breadcrumb Reading: Bb Test
E Field: Single Charge
What is the magnitude of the E field 12 cm from a -72 μC charge? Be prepared to give a numerical answer as well as articulate units and direction.
Before Next Class:
Assignment HW: Bb Test
E Field on Axis of Dipole:
Determine the total E field at a point along the axis (the line through the charges) that is a distance x away from the midpoint of the dipole. The charges are +4 nC and -4 nC and are separated by a distance of 14 mm. You should understand your solution well enough to be able to determine the numerical value of the field for any value of x. The thoughtful student will explore whether their solution can be simplified when x >> 14 mm.
Assignment HW: Bb Test
E Field at Midpoint of Side of Square Quadrupole:
Two charges (q) on opposite corners are positive and 2 are negative. All have a magnitude of 100 nC. The sides of the square are of length L. Determine the magnitude and direction of the total E field in the center of each side between the charges. You should understand your solution well enough to be able to determine the numerical value of the field for any value of L and q.
Assignment HW: Bb Assignment
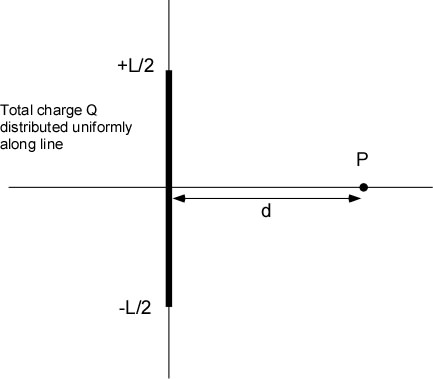
Line of Charge (Integration)
A line of charge is oriented along the vertical axis from -L/2 to + L/2. A total charge of Q is uniformly distributed along the line. Point P is a distance d along the horizontal axis from the center of the line of charge. Determine the total E field at P.
Looking Ahead:
Look ahead to the next Breadcrumb: Electric Potential I
Assignment Breadcrumb Reading: Bb Test
Potential:
The electric potential is defined to be the work done by the E field as a charge moves between two points divided by the magnitude of the charge moved (V = WAB/qmoved). There is an equivalent quantity called the gravitational potential (not potential energy!) which is defined similarly. What is the gravitational potential of a 4 kg mass on a 2 m high counter and what are it's units? Hint: In the end the 4 kg doesn't matter.
