Mood Brightener: ...more from Stay Homas. (Confination XVIII)
Sources of Magnetic Field (besides magnets!):
One challenge with trying to understand the sources of magnetic fields is that magnets and magnetic materials are quite complex and difficult to characterize. We can certainly talk about the strength of the B field at some distance from a magnet and use that as a way to define the strength of the dipole that is the magnet. Turns out to be tough. We will take a different approach that is the result of a happy accident in a classroom.
Hans Christian Oerstad was a Danish teacher who famously discovered that electric currents also create magnetic fields (B fields) while teaching a class. Because we can control currents relatively easily we develop a numerical understanding of the relationship between the current in a wire and the B field it creates.
As we did with E fields we need to distinguish between the moving charges that experience forces from the B field and moving charges (current) that create the B field. This is another way in which it seems incredibly likey that E and B fields are fundamentally connected.
Biot-Savart Law:
One challenge with figuring out a rule for something which depends on a current is that the source (the current) can't be a point object. Because of this the Biot-Savart Law is naturally takes on a differential form. Here is what those smart folks figured out....
Side Bar: Pronunciation: This behavior was first descibed by a couple of French scientists so it seems to me we ought to show some respect and pronounce their names correctly. Here is a link to Merriam-Webster's dictionary definition and pronunciation guide which matches this audio clip. You will find a lot of other stuff out there in the world but this is how we will pronounce it!
The Result:
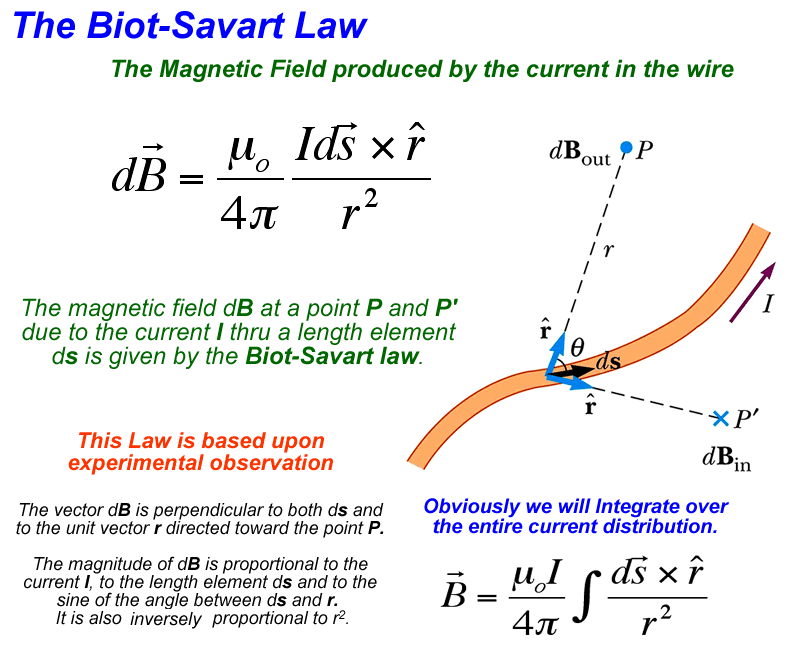
Units:
Who is this μ0 anyway? It's formal name is the magnetic permeability of free space and it's value is 4π 10-7 Tm/A. No doubt this seems like a suspiciously convenient value and it is. It turns out, because the Electric force and the Magnetic force are related to each other one of the constants can be freely chosen. Electric forces were studied first so it's constant got set and the magnetic constant was adjustable. The 4π is indeed related to spheres and is handy as we integrate. Other than that I don't know the history of how it's value was chosen.
Explorations:
A couple of things I'd want you to notice or think about.
Given the two vectors ds and rhat how to you apply the RHR to determine the directions of dB indicated in the image? Where is the angle that is part of the cross product. Remember the sin θ between the two vectors of the cross product.
Consider 4 points in space near a straight section of wire. One to the left of the wire, one to the right, one directly 'above' the wire, and one directly 'below' the wire. These four points lie along a circle with the wire at the center of the circle. (make a sketch!!)
Now consider the little bit of current at the center of that imaginary circle. What is the direction of dB at each of the 4 points and everywhere else along the circle? What is θ for this particular bit of current?
Now take a bit of the current/wire a bit 'before' the current arrives at the imginary circle. Repeat the exercise. Again for a bit of the current/wire a bit 'after' the current passes through the imaginary circle. Are you surprised by the result?
Observations:
It's interesting to note that the Biot-Savart Law has the same 1/r2 behavior as the sources of E fields! Note also the need for the use of the RHR in this case as well. This is why I prefer that you have a generic version of the RHR instead of a situation specific version.
We mostly use the Biot-Savart Law to determine the B field produced by specific current geometries that are common in physics and engineering. The most useful ones are are when the current moves through long straight wires, short straight wires, and around circular loops. This pdf from Akrem El-ghazal at the University of Waterloo in Canada lays out the details pretty nicely for future reference.
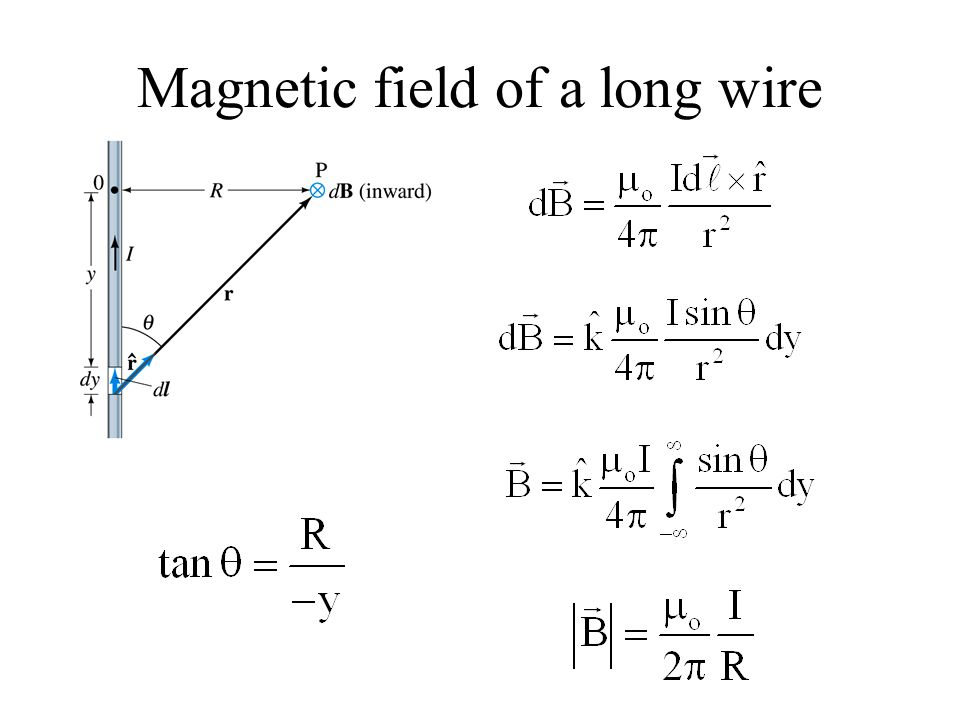
Infinite Wire (distance 'R' from wire)
What is the limit as the wire gets long of the previous expression?
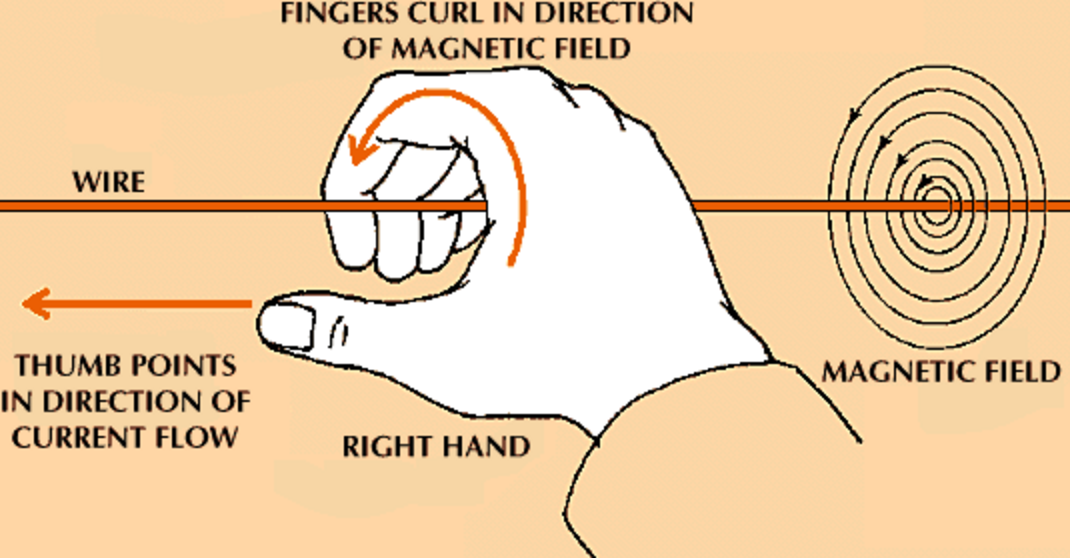
Right Hand Rules: RHR #2 for wires!
Two Parallel Wires:
Now we have an interesting situation to think about. Two wires running parallel to each other each carrying a current. The currents are moving charges and at the same time the currents create a magnetic field that creates a force on the moving charges. Consider this image...
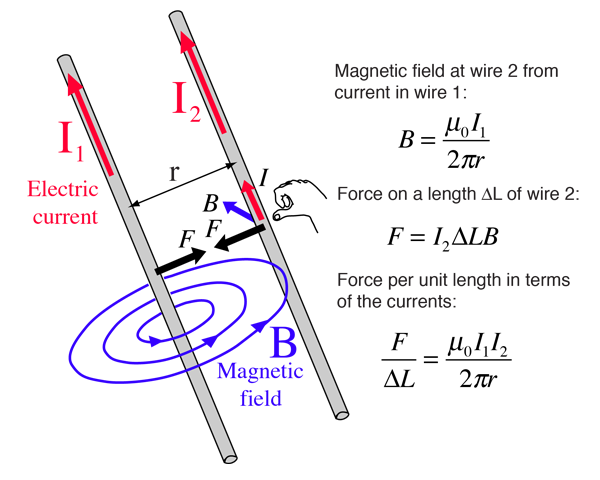
If you go back and look at our magnetic force rule FB = qvsin(θ)B you might notice that qv terms have the same units as IL where I is the current in the wire and L is the length of a piece of the wire. Thats where the force expression in the image above comes from. If the currents are flowing in the same direction the wires are pulled towards each other. What if the wires are going opposite directions?
Assignment Breadcrumb Reading: Bb Assignment
Sketch Magnetic Field Around Straight Wire:
Sketch the magnetic field (using field lines) in the region surrounding a straight wire carrying a current. I'm interested in how you will choose to represent this B field. Be sure to clearly indicate the direction of the current and the direction of the B Field lines.
Before Next Class:
Assignment HW: Bb Test
B Fields Under Power Lines:
You may have heard of concerns about magnetic fields from overhead power lines as a health risk. Careful research has shown this is NOT a thing. Calculate the B field on the ground 20 m under a power line carrying 100 A. Then calculate the B field under an electric blanket where you are 4 cm 'below' a wire carrying a current of 10 A?
Assignment HW: Bb Test
Overhead Wire Attraction:
If you look at the overhead wires that distribute power along the roads and highways of the US the wires are about 1 m apart. Assume for the moment the two adjacent wires are carrying 150 A each. What is the attactive force/m in this setting? Does it strike you that this is enough to noticeably move the wires sideways?
Looking Ahead:
Look ahead to the next Breadcrumb: Biot-Savart II
Assignment Breadcrumb Reading: Bb Test
B Field at Center of Coil:
Imagine you have a coil of wire 0.7 m in diameter (about the size of the tube in an MRI) with 30 A of current flowing through the wire. What is the B field at the center of the coil? Think about this compared to the 15 T B field that is required to make the MRI function successfuly.
