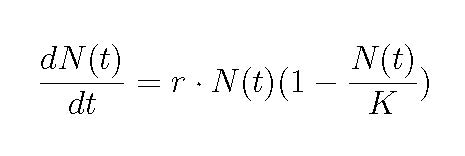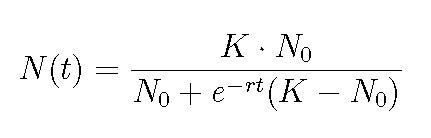Now that you've done a little work with periodic/harmonic motion here's a problem that asks you to extend that understanding a bit. You will need to tie together some concepts from PH211 about potential energy and springs. One way of thinking about this plot is that it is a time dependent energy bar chart (missing the KE term).
HW: Periodic DE
The graph shows the potential energy and the total energy of a 250 g mass in harmonic motion, horizontally, on a spring.

a) Where is the mass when the spring is unstretched?
b) Where is the mass when it changes direction? How did you figure this out?
c) What is the maximum kinetic energy of the mass?
d) What is the maximum velocity of the mass?
Periodic Motion Dynamics: Differential Equation Connection
Here's another example of periodic motion that is a little more contrived.
Sketch the motion, write the kinematic description and determine the maximum velocity and acceleration.
Activity: Now, make a complete freebody diagram of the mass on the air track and write Newton's 2nd Law for the horizontal and vertical parts of the motion of the object.
What relationship to this analysis do the words 'restoring force' have in this context?
You can rewrite the horizontal equation to look like a standard 2nd order linear homogenous differential equation. This assumes that you know what all of that vocabulary means. It is also an autonomous equation?
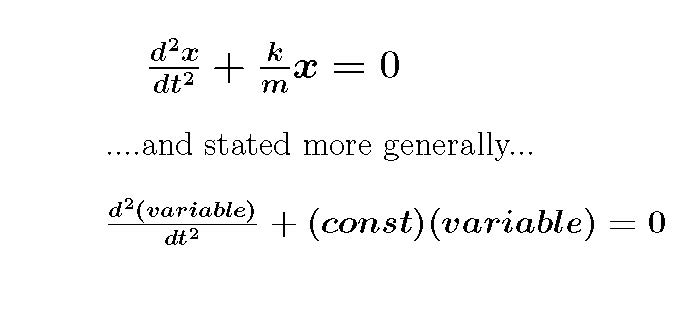
Trial Solution:
Once we have a differential equation (DE) there are a lot of tools from math classes that we might use to find a function that satisfies the equation. Finding this magical function is what 'solving' a differential equation is all about.
Sometimes we have an idea about what a function might be a solution to the DE. This is sometimes called a trial solution. What do we do if we have a trial solution? Here is the general approach....
i: Write the trial solution with as much generality as possible
ii: Take whatever derivatives are indicated in the equation
iii: Plug everything back into the original equation
iv: Examine terms (after factoring) for coefficients that must be 0 or some defined value
v: Apply boundary conditions.
Let's do this process for the equation that we have found for the horizontal part of the motion of the spring sled.
i: The solution is something where the second derivative is very similar to the original function so that it can cancel the original function. There are a couple of possibilities including eat and cosine or sine. Lets try (trial function) a cos() function. The most general form of a time dependent cos() function might look like this (A, D, and C are constants):
x1(t) = A cos (ωt +D) + C
Will the process still work if C = C(t)? Does x2(t) = A sin (ωt +D) + C work as well? Does x3(t) = x1(t) + x2(t) work also? What does this have to do with MTH 256? Second order DE's have two independent solutions and cos() and sin() are two independent (orthogonal) solutions!
Take Homes: Remember!
For a spring system:
ω2spring = k/m or ωspring = (k/m)1/2 = 2πf = 2π/T
or more usefully....
T = 2π(m/k)1/2
For all systems described by the DE shown above:
ω2 is always equal to the coefficient (constant) in front of the linear variable term.
HW: Periodic DE
The following differential equation is called the logistic equation and it describes a population that has a death rate that depends on how big the population is (crowded).
What are the units for each term and constant in this expression?
The solution to this logistic equation is purported to be....
Show that this solution does indeed work (if it does) or fail (how?). This as a trial solution. Use our process to test it.
What does this solution say about the population of whatever this creature is at t=0 and "after a long time"? Look at the solution first and then think what the differential equation has to say......does this make sense in the physical world?
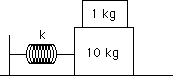
Activity: Consider the following HW problem. What is the freebody diagram for the 1 kg block and why is there a maximum amplitude where it can maintain it's position?
HW: Periodic DE
Two blocks with the masses shown are moving in SHM on a frictionless table. The coefficient of friction between the blocks is 0.40 and the spring constant is 200 N/m. What do you expect to happen to the period if the 10 kg mass is increased? Why? What do you expect to happen to the period if the spring constant is increased? Why? What is the maximum amplitude of the oscillation where the blocks do not move relative to each other? (You'll need to do a freebody and use Newton's Laws as well as the new material)
Side Note: Fourier Analysis
Falstad's Math and Engineering Applets: When these stop working I'm going to be very sad....
[insert video here to capture some of Falstad's applet]
What is the point of this discussion? What does the following video have to do with it?
Back to the Pendulum:
Freebody diagram, Newton's 2nd ...blah, blah,....leading to the differential eqn!(this is a lot longer than it looks!)
[insert video here -- not quite ready...]
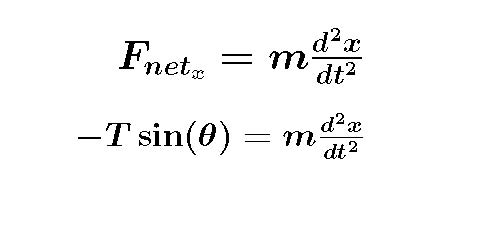
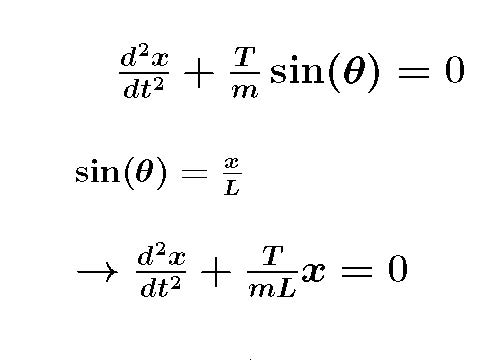
and then in the y.....
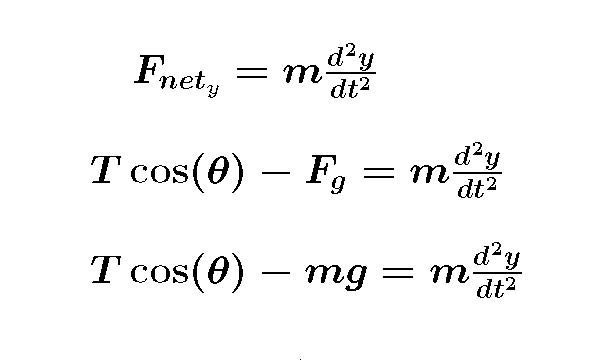

Is it a linear 2nd order differential homogeneous equation? The x direction looks pretty good but the y direction much less so. If you look at your freebody diagram you can see that T is not constant as the pendulum swings back and forth. This means even in the x direction the DE doesn't meet the expectations of the simple harmonic oscillator equation we discussed at the beginning of this breadcrumb.
What to do?
It is important to understand that in applied sciences (engineering) and often in physics we will make simplifying assumptions to see if we can gain some insight into the 'problem'. This very similar to what we did when we neglected air drag when we did those projectile problems back in PH211. In this case one could argue that as long as the angle is small cos(θ) ≅ 1 which means since T cos(θ) = mg then T ≅ mg under these circumstances- yikes! Let's see what happens if we make this approximation....
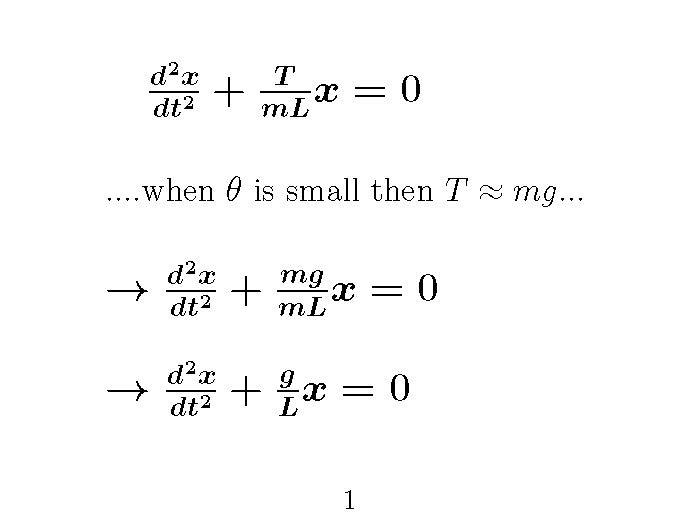
...and...
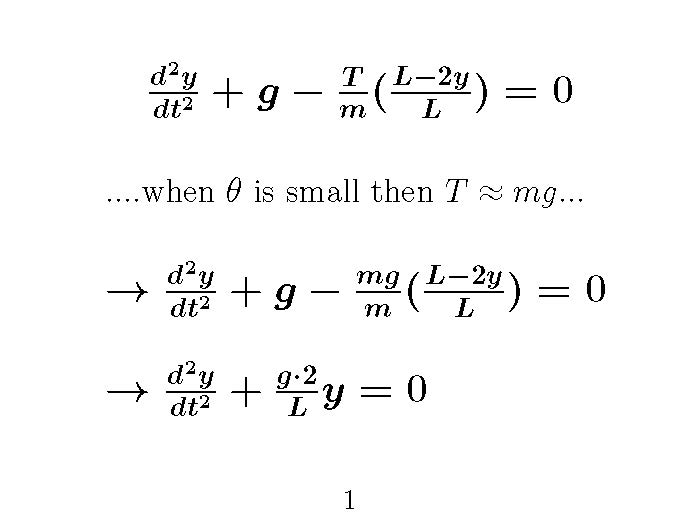
You will notice that in both cases this approximation cleans up the differential equation and gives it exactly the form of the simple harmonic oscillator equation. We often decribe this as the small angle approximation. We will use another version of this again later in the term.
Notice that....
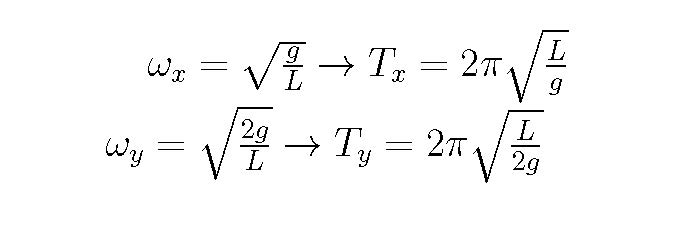
...which says that the period of the motion in the horizontal direction is twice that of the horizontal direction as we observed in the pendulum video. Sweet!!
Take Home: Remember!
For a simple pendulum:
ω2pendulum = g/L or ωpendulum= (g/L)1/2 = 2πf = 2π/T
Loans and Savings: A Bonus Exploration
Now let's look at another situation that is described by a differential equation -- what is the mathematical description of a loan that you repay the principal with monthly payments? Think about the rate of change of the principal you owe....here is a way of expressing that where N(t) is what you owe and r is the fixed rate of interest.
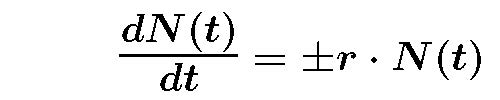
As you watch your mathematical description evolve think about the units of each term and what it actually means. Consider the impact of monthly compounding -- what does that even mean? How is the the same or different when compared to a savings account? Did we include any actual payment in this mathematical description? What do we need to change to include a payment?
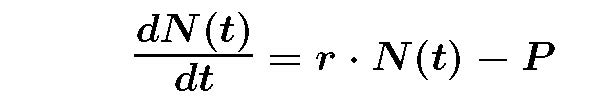
Write your differential equation in the traditional mathematical form and describe the characteristics of the equation. I have included here both the homogeneous and inhomogeneous versions.
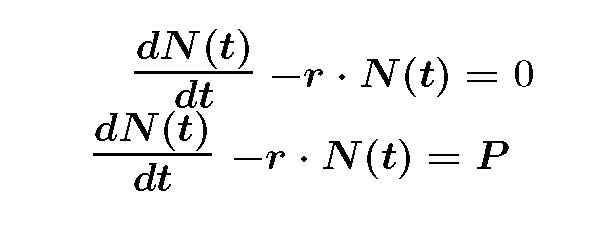
What is a possible trial function that has the same characteristics as the function described by the differential equation? As we talked about in class think about how to describe the relationship between the function N(t) and it's derivative. What function do you know whose derivative is the same as the original function except for a constant? Perhaps an exponential? Another example of using our approach to trial functions....
Here is a very general exponential function that we could use as a trial function...
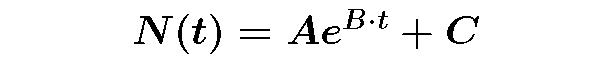
Running it through our process for the homogeneous equation we can see that C = 0, B = r, and A can be anything.
What are the boundary/initial conditions that apply to this problem? At t = 0 N(t=0) should give us the initial value of our loan which leads us to A = N(t=0) or N0.
Here is a more formal explanation of the differential equations and solutions for the loan problem for future reference.
Assignment: HW: Periodic DE
Turn in the various (3) homework problems in this breadcrumb.
Assignment: Reading
Go on to Damped and Driven breadcrumb to move to our discussion of the dynamics of periodic behavior.