Standing Wave Applications:

There are many settings where standing waves come in to play. We will consider a subset of those which are mostly 1D. Everything that we do can be extended to 2D and 3D though the math gets much more exciting.

When Boundary Conditions are NOT the Same:

So when does this happen? There are a couple of classic examples. For sound waves a tube that is open at one end and closed at the other (sort of like a coke bottle) is an example. For a physical wave a flexible stick held at one end is also an example. Let's run through our process for a setting of this type.

Activity: What are the wavelengths and frequencies for the standing waves in a tube that is open at one end and closed at the other?

When you're done these are the patterns you will find (hopefully)

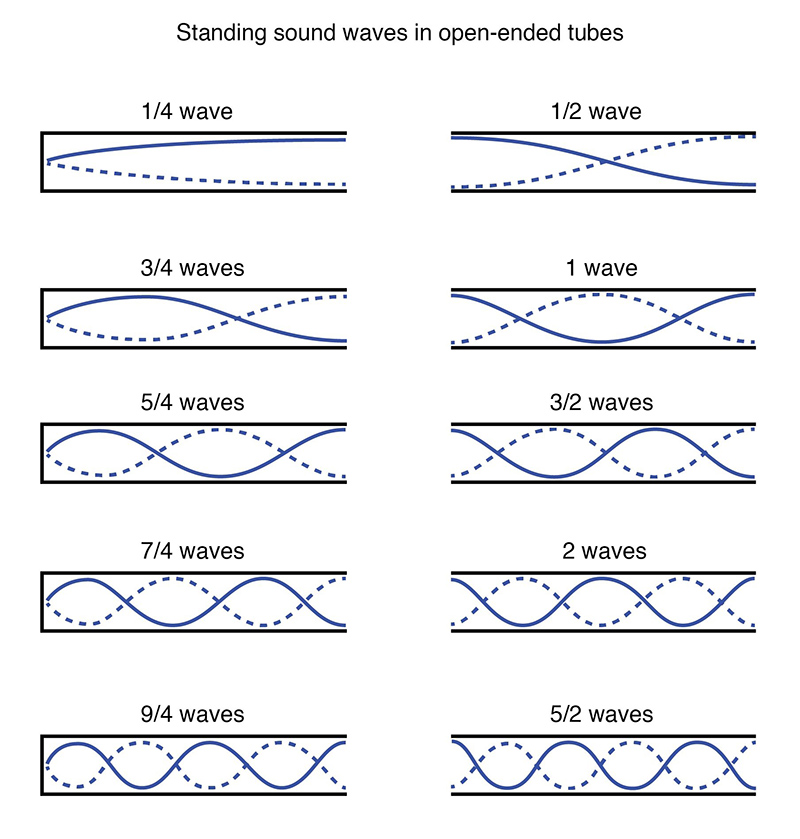
Pulling it all together and describing all the possible wavelengths and frequencies we get the following key results for the possible wavelengths of the standing waves...

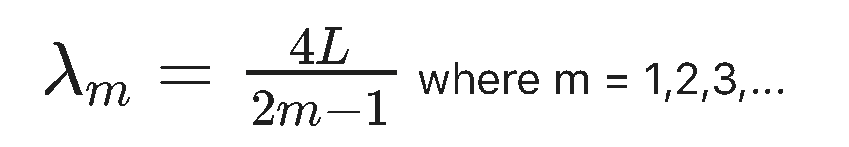
and this expression for the possible frequencies of the standing waves....

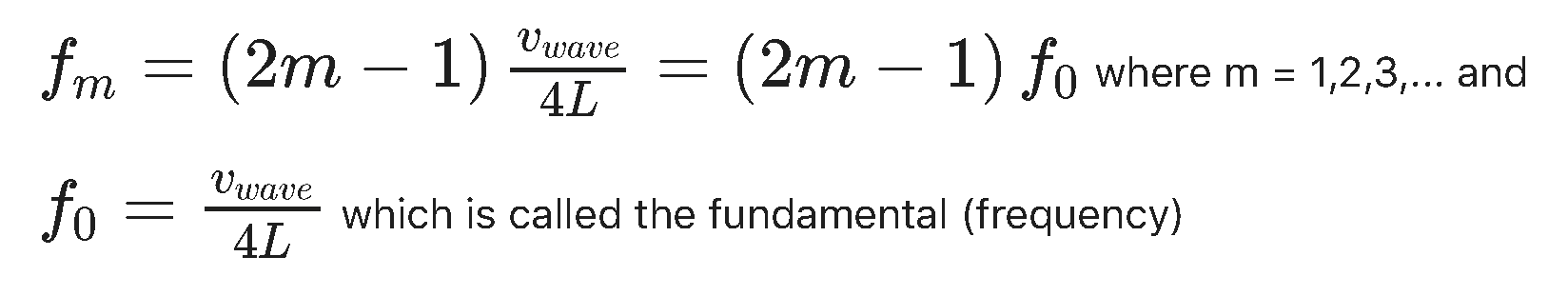
You will notice that instead of having every multiple of the fundamental frequency we only have the odd multiples (1, 3, 5, ....) of the fundemental. The tradition in math and physics is to indicate odd values by using 2m-1 where m = 1, 2, 3,..... I point this out because any time you see a 2m-1 or 2m+1 in math, physics, or engineering you should think 'odd values' as a first response.

Asymmetric Boundary Conditions:

The expressions above apply to any application where the boundary conditions are asymmetric (opposite) at each end. As before, if there are any other constraints on the problem then this solution might not apply.

Boundary Conditions and Constraints:

Our next example contains boundary conditions AND additional contraints. A marimba bar is an example of a class of objects like xylophones, vibraphones, and garden chimes which are struck to generate a wave travelling in bar to produce standing waves. To support a horizontal object that you are going to strike with a mallet it needs to be supported at two points. From a boundary condition perspective the ends are free to move so for a transverse wave the standing wave patterns look identical to a tube that is open at both ends (symmetric BC's). Here are the first three harmonics.

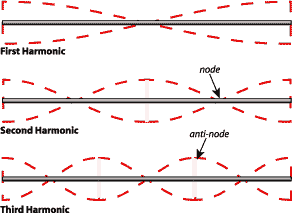
If you consider where you might want to support this bar in two places the points 1/4 of the way in from the end of the bar seem pretty reasonable. Notice that they are symmetric. In a general sense this explains the construction of a marimba bar. The details get much more complicated because the bars are usually hollowed out underneath to provide more amplitude of motion and this changes the wave speed (non-uniformly) which changes the standing wave patterns and frequencies. If such things fascinate you here is a link to a very nice discussion of how you really do it.

Does this offer an explanation for where the strings support these meditation chimes?

 

What would happen if the bars were slid a little to the side so the support points are different distances from the ends? Do you see that this changes the possible standing wave patterns and possibly eliminates most options? Almost any linear object will ring very nicely as a chime if you support it at the correct point which will have to be a node.

The same thing is true for garden chimes. You can't support it in the middle because it can't balance. 1/4th of the way from one end works much better. Even cheap electrical conduit from the hardware store will ring pretty nicely if you support it at the right point. If you want to have some fun building your own chimes Lee Hite has generously made his design handbook for chimes available to all - thanks Lee!

HW: Standing Waves More Applications

The marimba bar over a resonator is 40 cm long and is supported 10 cm from each end. If the frequency of the sound produced by the bar is 200 Hz what is the speed of the wave traveling up and down the marimba bar? How long will the resonator tube underneath the bar need to be if it is capped at the bottom end (open at the top)

HW: Standing Waves More Applications

A tall building is just a stick waving in the air that is rigidly connected to the ground. Assume you have a 60 story building that is being driven by an earthquake at it's base. What are the shapes of the first three standing waves the building might form (sketch!!). Which floors of the building would be under most stress in each case?

Ruben's Tube:

Lots of people have seem a Ruben's Tube (flame tube) Can you explain the physics now? There is a speaker at one end of the tube which has small holes drilled all along it.

 

More than 1 D:

Standing waves are not just a one dimensional effect. We just always begin our investigations into things as simply as possible. The mathematics for solving 2 D and 3 D problems is much more complex but the concepts are the same. There are particular frequencies that are associated with wave pattern that depend on boundary conditions and constraints. Chaladni plates are a relatively simple 2D system. If we are meeting f2f we will undoubtedly do this in class. Otherwise here is a video of the effect. This video also includes a stunning example of 3D acoustic standing waves supporting light bits of foam in space -- too cool!

 

Here is a 2D version of the Ruben's tube. It's not as satisfying but still interesting...

Mickey Mouse and Darth Vader:

The penultimate example for our discussion of standing waves centers around the role of standing waves in the Mickey Mouse effect when you inhale helium. Our heads are a 3D resonant chamber that involve our throats, our mouths, and our sinuses. Changes to any of those change the standing wave frequencies for the 'swiss cheese' of our head. That's why our voices sound different when we have a cold that stuff up our sinuses. There are also effects from our vocal cords. Let's work our way into this. Consider first the collection of frequencies that are found in a trumpet note. This is a 1D standing wave system so we expect it to show features like what we have discussed.

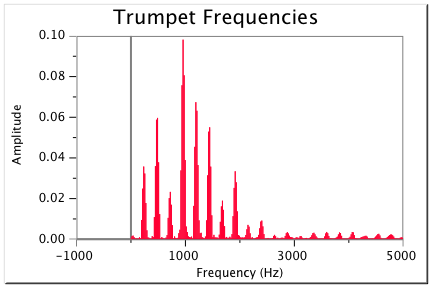
See all the well defined frequencies? With a little effort you can see that every peak (representing a 'strong' frequency) is a multiple of the fundamental. This is also evident in the equal spacing of the peaks. The amplitude of the peaks is also characteristic of the trumpet.

Here is a similar spectral analysis (called a fast fourier transform - fft) for a particular person.

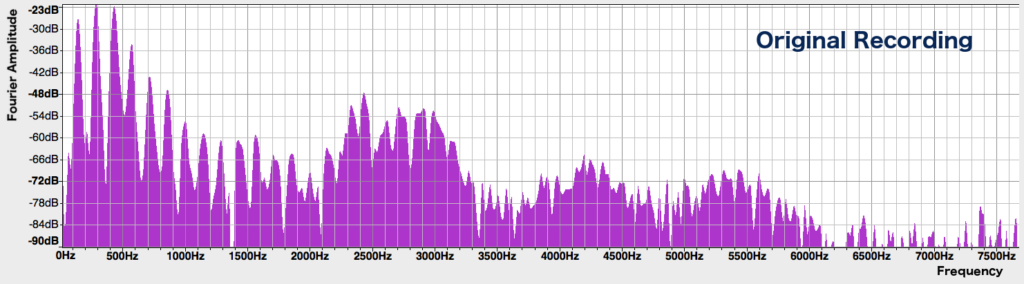
Again, notice the pattern of peaks that are indicative of a standing wave or resonant effect. This system is much more complicated and the peaks are not equally spaced. Never the less there are all the indications of a standing wave process.

Now remember that the wavelengths of the standing waves are determined by the physical characteristics of the string or chamber. Those won't change no matter what the medium is. A heavier string of lenght L has the same standing wave wavelengths as a lighter string of the same length L. The frequencies will be different ( f = v_wave/λ) because the wave speed will be different. Same is true of the frequencies rattling around in our heads. The wavelengths that form the 3D standing wave patterns are consistent but what if I fill my head with a gas that has a different speed for carrying sound waves? Yup -- the frequencies change! He is a light gas that moves very quickly so sound travels very fast. Sulfer Hexaflouride (SF₆) is a very heavy gas which makes the speed of sound very slow. Can you anticipate what will happen?

SAFETY NOTE: In both cases there is some risk because neither He or SF₆ keep the body going so if either one stays in your lungs you will suffocate - not good! We don't usually worry about He because its very light, so it floats up, and moves very fast so it rattles it's way out of your lungs quite quickly. Still dangerous if you keep sucking down helium over and over again. SF₆ in MUCH scarier. It's heaver than air so when you suck it into your lungs it sinks to the bottom and doesn't leave. It's moving much slower than air which also makes it settle in your lungs. Suffocation is a real risk and you may not have noticed that Adam is yelling the clip partly to expell the SF₆ as fast as he can. They also cut the clip right afterwards and he bent over and pushed the air out of his lungs over and over again for about a minute. That is why you should not try this -- having somebody standing around watching you pass out is NOT going to get the SF₆ out of your lungs. Do I make myself clear?

Wave Tank:

For oceanographic research purposes an enormous 2 dimensional wave tank was built to create controllable waves for testing devices going into the ocean. The standing wave patterns start at about 1:00 with the concentric wave spike (this happens in your coffee cup sometimes when you're driving). There are other fascinating ones if you watch it all the way through.

 

Here is the 'how it works' video.

 

Sidebar: Theremin

The Theremin is an instrument that uses electrical resonance to control pictch and loudness. Deep inside the electronics is a electrical standing wave system whose characteristics are affected by the placement of the players hands near the two antennae. I shared this TED video of Pamelia Kurstin (now Stickney) demonstrating and explaining how this instrument is played. She has since moved to Vienna and performs in various contexts around the world. If this stuff fascinates you here is the link to her current homepage.

HW: Standing Waves More Applications

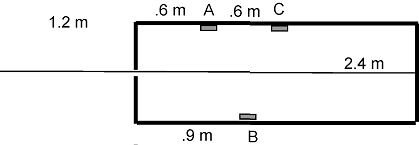
This is one of those problems that fascinate me and an old test problem. You are confronted with a box 2.4 m long with a rope hanging out of a hole at one end. The rope outside the box is 1.2 m long and the box has a transparent top so you can see that the rope is tied to the other end of the box. Along the side of the box are a number of switches that you need to turn on in a particular order to win the $10E^.10⁶ prize. The switches must be turned on in alphabetical order. Once the switch has been turned on it stays on so you don't have to worry about hitting it again. You can generate standing waves in the box by shaking the rope outside the box. Where you hold the rope will be a node but you don't have to hold it at the end.

I) What is the shape of the standing wave, inside and outside the box, you could use to turn on switch A without turning on any others?

II) If the speed of the wave is observed to be 4 m/s what is the frequency of the standing wave which turns on switch B (but not C)? Sketch the wave both inside and outside the box.

III) What is the shape, inside and outside the box, and frequency of the wave which you could use to turn on switch C? Are there other switches that will be hit? Sketch what has to happen in the box and be prepared to shorten your grip on the rope outside the box for this!

Assignment: HW: Standing Waves More Applications

Turn in the various (3) homework problems in this breadcrumb.

Assignment: Reading

Go on to the Doppler Shift breadcrumbs as we move on to a different wave behavior.